250 câu trắc nghiệm Ứng dụng đạo hàm để khảo sát hàm số cơ bản (P6)
-
36092 lượt thi
-
30 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Hàm số y = f(x) liên tục trên R và có bảng biến thiên dưới đây. Khẳng định nào sau đây là đúng?
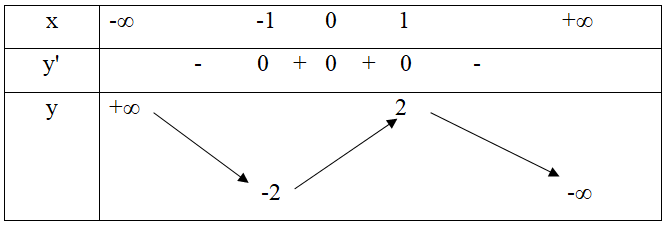
Đáp án : C.
Câu 2:
Cho hàm số y = f(x) có bảng biến thiên như hình vẽ. Khẳng định nào sau đây là khẳng định sai?
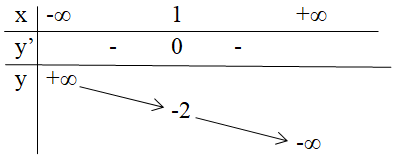
Đáp án B.
Từ bảng biến thiên của hàm số ta thấy hàm số nghịch biến trên R, hàm số không có cực trị và
Vậy khẳng định sai là “Hàm số đạt cực tiểu tại x = 1”
Câu 3:
Hàm số y = 1/3.x3 + x2 - 2/3 có
Đáp án A.
y' = x2 + 2x
Do a > 0 nên hàm số đạt cực đại tại x = -2, đạt cực tiểu tại x = 0
Câu 4:
Đồ thị hàm số y = x3 – 3x2 – 9x – 5 có điểm cực tiểu là
Đáp án A.
Ta có: D = R và y’ = 3x2 – 6x – 9, y’’ = 6x – 6.
Do đó y’ = 0 ⇔ x = -1 ∨ x = 3.
Do y’’(-1) = -12 < 0 và y’’(3) = 12 > 0 nên hàm số đạt cực tiểu tại x = 3.
Đồ thị hàm số y = x3 – 3x2 – 9x – 5 có điểm cực tiểu là (3; 32)
Câu 5:
Hàm số y = 2x4 – 8x3 + 15
Đáp án C.
Ta có D = R và y’ = 8x3 – 24x2, y’ = 0 <=> x = 0 ∨ x = 3.
BBT
Vậy hàm số nhận điểm x = 3 làm điểm cực tiểu
Câu 6:
Hàm số y = -x4 – 2x2 + 3 có bao nhiêu điểm cực trị?
Đáp án A.
y’ = -4x3 – 4x
y’ = 0 <=> x = 0.
Bảng biến thiên
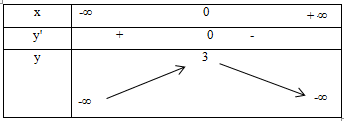
Câu 7:
Biết hàm số y = x3 – 3x + 1 có hai điểm cực trị x1; x2 Tính tổng x12 + x22.
Đáp án C.
Tập xác định: R
y = x3 – 3x + 1 => y’ = 3x2 – 3 <=> x = ± 1.
Vậy hai điểm cực trị thỏa mãn: x12 + x22 = 2
Câu 8:
Hàm số y = x4 – 4x2 – 5
Đáp án B.
Ta có: y’ = 4x3 – 8x
y’’ = 12x2 – 8
y’’(0) = -8 < 0
Suy ra x = 0 là điểm cực đại
Câu 9:
Hàm số nào trong bốn hàm số được liệt kê ở bốn phướng án A, B, C, D dưới đây, không có cực trị?
Đáp án D
Suy ra hàm số nghịch biến trên các khoảng xác định của nó do đó đồ thị hàm số không có cực trị
Câu 10:
Cho hàm số y = f(x) xác định, liên tục trên đoạn [-2;3] và có đồ thị là đường cong trong hình vẽ bên. Tìm số điểm cực đại của hàm số y = f(x) trên đoạn [-2; 3]
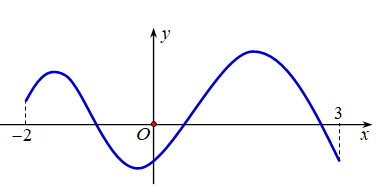
Đáp án C.
Quan sát đồ thị hàm số, ta thấy có hai điểm cực đại thuộc đoạn [-2; 3]
Câu 11:
Trong các hàm số sau, hàm số nào có hai điểm cực đại và một điểm cực tiểu?
Đáp án C.
Hàm số bậc 4 có hai điểm cực đại và một điểm cực tiểu
Câu 12:
Hàm số y = x3 – 3x2 – 1 đạt cực đại tại?
Đáp án A.
Tập xác định D = R.
y' = 3x2 – 6x
y’ = 0 <=> x = 0 hoặc x = 2.
Bảng biến thiên:
Hàm số đạt cực đại tại x = 0
Câu 13:
Cho hàm số y = x4 – 2x2 + 2. Kết luận nào sau đây sai?
Đáp án A.
Tập xác định D = R.
y' = x3 – 4x
y’ = 0 <=> x3 – 4x = 0 <=> x = 0 hoặc x = -2 hoặc x = 2.
Bảng biến thiên
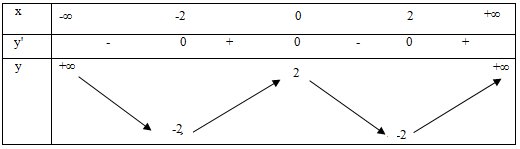
Hàm số đồng biến trên các khoảng (-2; 0) và (2; +∞) nên đáp án A sai
Câu 14:
Hàm số nào sau đây có 2 cực đại?
Đáp án A.
Hàm số bậc 4 trùng phương y = ax4 + bx2 + x có hai cực đại khi a < 0, b > 0
Câu 15:
Cho hàm số y = f(x) xác định, liên tục trên R và có bảng biến thiên.
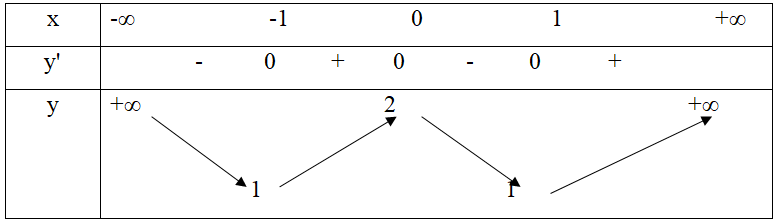
Khẳng định nào sau đây là sai?
Đáp án A.
Điểm M(0; 2) được gọi là điểm cực đại của đồ thị hàm số.
Câu 16:
Cho hàm số y = f(x) có đồ thị là hình vẽ bên. Trong các khẳng định sau, khẳng định nào sai?
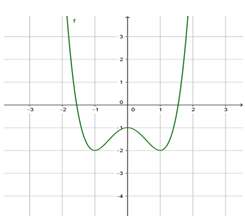
Đáp án B.
Hàm số có ba điểm cực trị, đạt cực tiểu tại các điểm x = 1 và x = -1 và hàm số nghịch biến trên các khoảng (-∞; -1) và (0; 1). Hàm số đạt cực đại tại điểm có hoành độ x = 0
Câu 17:
Hàm số nào sau đây có xCĐ < xCT:
Đáp án B.
Hàm số có xCĐ < xCT nếu là hàm số bậc ba thì phải có hệ số a > 0 nên ta loại C.
Ta loại đáp án A vì hàm số y = x3 + 3x – 1 không có cực trị (y’ = 3x2 + 3 > 0,∀x ∈ R).
Loại đáp án D vì hs y = x4 + x2 – 1 chỉ có 1 cực trị.
Vậy ta chọn đáp án B
Câu 18:
Khẳng định nào sau đây đúng khi nói về hàm số y = x4 + 4x2 – 2?
Đáp án A.
Tập xác định: D = R
Ta có: y’ = 4x3 + 8x => y’ = 0 ó x = 0
Vì y = x4 + 4x2 – 2 là hàm số trùng phương có hệ số a = 1 > 0 và y’ = 0 có một nghiệm x = 0 nên hàm số đạt cực tiểu tại x = 0
Câu 19:
Cho hàm số y = f(x) có đồ thị là đường cong trong hình vẽ bên. Hàm số f(x) đạt cực tiểu tại điểm nào dưới đây?
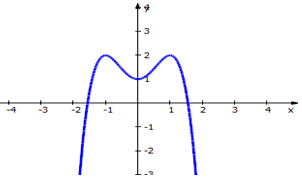
Đáp án D.
Hàm số f(x) đạt cực tiểu tại điểm x = 0
Câu 20:
Kí hiệu m, M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số trên đoạn [1;4]. Tính giá trị biểu thức d = M – m
Đáp án A
Suy ra hàm nghịch biến trên từng khoảng xác định, do đó hàm số nghịch biến trên đoạn [1; 4]. Vậy m = y(4) = 1; M = y(1) = 4 => d = M – m = 4 – 1 = 3
Câu 23:
Trên đoạn [-1; 1], hàm số y = -4/3.x3 – 2x2 – x – 3
Đáp án B.
Hàm số liên tục trên [-1; 1]
Ta có y’ = -4x2 – 4x – 1
y' = 0 <=> -4x2 – 4x – 1 = 0 <=> x = -1/2
Vậy y(1) = -22/3 , y(-1) = -8/3, y(-1/2) = -17/6
Câu 25:
Tìm M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = x3 – 3x2 – 9x + 35 trên đoạn [-4;4] là
Đáp án A.
Hàm số liên tục trên đoạn [-4;4]
y' = 3x2 – 6x – 9, y’ = 0 => x2 – 2x – 3 = 0
Ta có y(-4) = -41; y(4) = 15; y(-1) = 40; y(3) = 8
Vậy M = max[-4;4]y = 40 và m = min[-4;4]y = -41
Câu 26:
Hàm số y = x3 – 2x2 – 7x + 5 có giá trị nhỏ nhất là m và giá trị lớn nhất là M trên đoạn [1;3]. Khi đó tổng m + M bằng
Đáp án A.
y = x3 – 2x2 – 7x + 5
Hàm số xác định và liên tục trên đoạn [1;3].
y' = 3x2 – 4x – 7
Câu 28:
Giá trị lớn nhất của hàm số y = x3 – 3x + 1 trên [0; 1] là:
Đáp án D.
Tập xác định: D = R
y' = 3x2 – 3 => y’ = 0
y(0) = 1, y(1) = -1
Hàm số max[0;1]y = y(0) = 1
Câu 29:
Tìm giá trị nhỏ nhất của hàm số trên đoạn [-3;1].
Đáp án C.
Hàm số xác định và liên tục trên đoạn [-3;1].
y’ = 0 <=> x = 0 ∈ [-3;1].
Ta có: y(-3) = 7, y(0) = 2, y(1) = 3
Vậy min[-3; 1]y = 2.
Câu 30:
Hàm số y = x3 – 3x2 + 3x + 2017
Đáp án A.
y = x3 – 3x2 + 3x + 2017 => y’ = 3x2 – 6x + 3 = 3(x – 1)2 ≥ 0, ∀x ∈ R
Vậy hàm số đồng biến trên tập xác định
