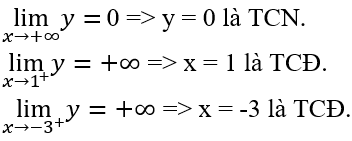30 câu hỏi trắc nghiệm thuộc 250 câu trắc nghiệm Ứng dụng đạo hàm để khảo sát hàm số cơ bản (P8)

Câu 1:

Tìm phương trình đường tiệm cận ngang của đồ thị hàm số $y = \frac{3 x + 2}{x + 1}$

A. x = -1.

B. x = 1.

C. y = 3.

D. y = 2.

Xem đáp án

Đáp án C

Câu 2:

Đồ thị của hàm số $y = \frac{x + 1}{x^{2} + 2 x - 3}$ có bao nhiêu tiệm cận ?

A. 1

B. 0.

C. 3

D. 2.

Xem đáp án

Đáp án C.

Ta có: D = R \ {1 ; -3}

Câu 3:

Số đường tiệm cận của hàm số $y = \frac{1 - x}{1 + x}$ là

A. 0

B. 1.

C. 2

D. 3

Xem đáp án

Đáp án C.

Hàm số đã cho có tiệm cận đứng là đường thẳng x = -1; tiệm cận ngang là đường thẳng y = -1. Tóm lại là nó có hai đường tiệm cận.

Câu 4:

Số tiệm cận của đồ thị hàm số $y = \frac{2 x + 1}{x - 2}$ là:

A. 1.

B. 0

C. 2.

D. 3.

Xem đáp án

Đáp án C.

Ta có nên đồ thị hàm số có đường tiệm cận ngang là y = 2.

Và nên đồ thị hàm số có đường tiệm cận đứng là x = 2.

Vậy đồ thị hàm số có 2 đường tiệm cận.

Chú ý: đồ thị hàm số (c ≠ 0; ad – bc ≠ 0) luôn có 2 đường tiệm cận.

Câu 5:

Tìm số đường tiệm cận của đồ thị hàm số $y = \frac{3 x - 2}{x}$

A. 0

B. 1

C. 2.

D. 3

Xem đáp án

Đáp án C

=> Đồ thị có đường tiệm cận ngang y = 3

=> Đồ thị có đường tiệm cận đứng x = 0

Vậy số đường tiệm cận hàm số là 2

Câu 6:

Tìm số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số $y = \frac{2 x + 1}{x - 1}$

A. 1.

B. 0.

C. 2.

D. 3.

Xem đáp án

Đáp án C

Câu 7:

Cho hàm số $y = \frac{\sqrt{1 - x}}{x^{2} - 1}$ Mệnh đề nào dưới đây đúng?

A. Đồ thị hàm số đã cho có đúng một tiệm cận đứng.

B. Đồ thị hàm số đã cho có đúng hai tiệm cận đứng.

C. Đồ thị hàm số đã cho không có tiệm cận ngang.

D. Đồ thị hàm số đã cho có đúng hai tiệm cận ngang

Xem đáp án

Đáp án B

Vậy hàm số có đúng 2 tiệm cần đứng

Câu 8:

Đồ thị của hàm số $y = \frac{x + 1}{x^{2} + 2 x - 3}$ có bao nhiêu tiệm cận?

A. 1

B. 2

C. 3

D. 4

Xem đáp án

Đáp án C.

=> đồ thị hàm số có 2 tiệm cận đứng x = 1; x = -3

Vậy có 3 đường tiệm cận

Câu 9:

Số đường tiệm cận cận của đồ thị hàm số $y = \frac{x - 2}{3 - x}$ là:

A. 2.

B. 3.

C. 1.

D. 0.

Xem đáp án

Đáp án A

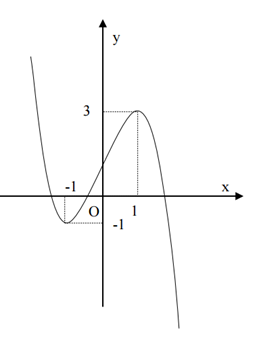
Câu 10:

Đường cong (C): $y = \frac{5 x + 2}{x^{2} - 4}$ có bao nhiêu tiệm cận?

A. 4

B. 2

C. 3

D. 1

Xem đáp án

Đáp án C

Đồ thị có hai tiệm cận đứng là x = 2 và x = -2 và có một tiệm cận ngang là y = 0

Câu 11:

Số đường tiệm cận của đồ thị hàm số $y = \frac{1 - x}{1 + x}$ là

A. 1.

B. 2.

C. 3.

D. 0.

Xem đáp án

Đáp án B.

Đồ thị hàm số có tiệm cận đứng là x = -1 và tiệm cận ngang là y = -1.

Số đường tiệm cận của đồ thị là 2.

Câu 12:

Cho hàm số y = f(x) có $\lim_{x \to 0^{+}} f (x) = - \infty$ và $\lim_{x \to 2^{+}} f (x) = - \infty$

Khẳng định nào sau đây là khẳng định đúng?

A. Đồ thị hàm số đã cho không có tiệm cận đứng.

B. Đồ thị hàm số đã cho có đúng một tiệm cận đứng.

C. Đồ thị hàm số đã cho có hai tiệm cận đứng là các đường thẳng y = 0 và y = 2.

D. Đồ thị hàm số đã cho có hai tiệm cận đứng là các đường thẳng x = 0 và x = 2.

Xem đáp án

Đáp án D.

Đồ thị hàm số đã cho có hai tiệm cận đứng là các đường thẳng x = 0 và x = 2

Câu 13:

Số đường tiệm cận của hàm số $y = \frac{\sqrt{1 + x^{2}}}{1 - x}$ là:

A. 1.

B. 2.

C. 0

D. 3

Xem đáp án

Đáp án D.

Tập xác định: D = R \ {1}

Tiệm cận đứng:

=> x = 1 là tiệm cận đứng

Tiệm cận ngang:

=> y = 1 là tiệm cận ngang

Vậy đồ thị hàm số có ba tiệm cận

Câu 14:

Hàm số y = f(x) có đồ thị như hình vẽ bên. Khẳng định nào sau đây là khẳng định đúng?

A. Đồ thị hàm số có tiệm cận đứng là x = 1 và tiệm cận ngang là y = -2.

B. Hàm số đồng biến trên các khoảng (-∞; -2), (-2; +∞).

C. Đồ thị hàm số cắt trục hoành tại điểm M(0; -1).

D. Hàm số nghịch biến trên các khoảng (-∞; -2), (-2; +∞).

Xem đáp án

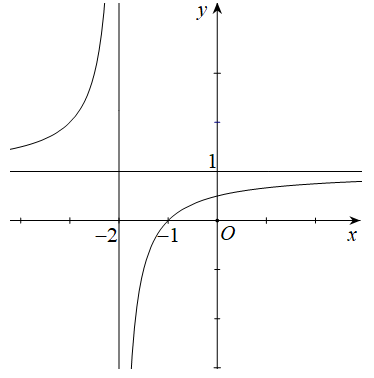
Đáp án B.

Ta thấy hàm số đồng biến trên các khoảng (-∞; -2), (-2; +∞)

Câu 15:

Cho hàm số y = f(x) có đồ thị như hình vẽ.

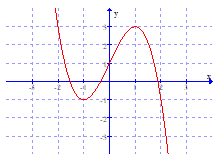
Hàm số y = f(x) đồng biến trên khoảng nào sau đây?

A. (0; +∞).

B. (-1; 1).

C. (-1; 3).

D. (1; +∞).

Xem đáp án

Đáp án B.

Hàm số đồng biến nếu x tăng thì giá trị y cũng tăng theo

Câu 16:

Đường cong trong hình vẽ dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?

A. y = x⁴ – 2x² – 1

B. y = x⁴ – 2x² + 1

C. y = x⁴ – 2x²

D. y = x⁴ – 2x² + 2

Xem đáp án

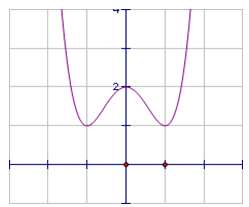
Đáp án D.

Ta thấy đồ thị hàm số đã cho cắt trục tung tại điểm A(0; 2).

Do đó đồ thị ở đáp án D là đáp án duy nhất thỏa mãn đầu bài

Câu 17:

Ðường cong trong hình dưới là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?

A. y = x⁴ – 2x² – 1

B. y = x⁴ – 2x² – 3

C. y = x³ – x² – 1

D. y = -x⁴ + 2x² + 1

Xem đáp án

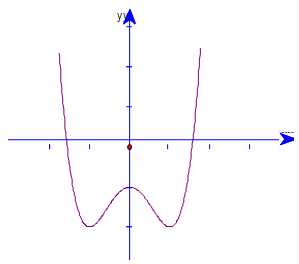
Đáp án A.

Nhìn vào hình vẽ ta thấy đây là đồ thị hàm số trùng phương với hệ số a > 0 nên loại phương án C và D.

Mặt khác ta thấy đồ thị cắt trục tung tại điểm có tọa độ (0; -1) nên ta có hệ số c = -1

Câu 18:

Đường cong hình bên là đồ thị của hàm số nào trong các hàm số sau?

A. y = x² – 1

B. y = x⁴ + 2x² – 1

C. y = -x⁴ – 2x² – 1

D. y = x³ + 2x² – 1

Xem đáp án

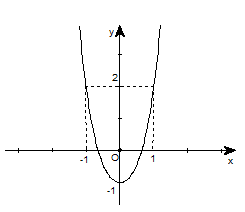
Đáp án B.

Nhìn hình vẽ ta loại phương án C và D vì phương án C là hàm trùng phương với hệ số a < 0, còn phương án D là hàm bậc ba.

Mặt khác chọn x = 1 thay vào phương án A và B, thì phương án A có y = 0 còn phương án B thì y = 2

Câu 19:

Đường cong hình bên là đồ thị của một hàm số. Hãy chọn khẳng định đúng

A. Hàm số đồng biến trên các khoảng (-∞; 1) và (1; +∞)

B. Hàm số nghịch biến trên R

C. Hàm số đồng biến trên R

D. Hàm số nghịch biến trên các khoảng (-∞; 1) và (1; +∞)

Xem đáp án

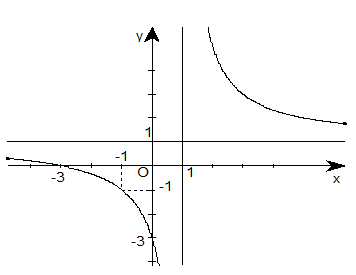
Đáp án D.

Dựa vào đồ thị ta thấy hàm số nghịch biến trên khoảng (-∞; 1) và (1; +∞).

Câu 20:

Đường cong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hàm số đó là hàm số nào?

A.

B.

C.

D.

Xem đáp án

Đáp án D.

Hàm số tiệm cận ngang y = 2 nên loại B.

Đồ thị hàm số cắt trục tung tại điểm (0; -1) nên loại A, C.

Câu 21:

Cho đồ thị sau

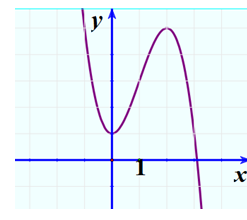
Hỏi hàm số nào sau đây có đồ thị ở hình trên?

A. y = x³ + 3x² + 1

B. y = -x³ – 3x² + 1

C. y = x³ – 3x² + 1

D. y= -x³ + 3x² + 1

Xem đáp án

Đáp án D.

Đồ thị có dạng của hàm số bậc ba với hệ số a < 0 nên loại A, C.

Đồ thị có hoành độ điểm cực đại dương nên Đáp án D

Câu 22:

Đường cong trong hình vẽ là đồ thị của hàm số nào dưới đây?

A. y = x⁴ – 2x² + 2

B. y = x³ – 3x² + 2

C. y = -x⁴ + 2x² + 2

D. Tất cả đều sai

Xem đáp án

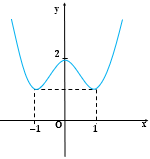
Đáp án A.

Vì đồ thị hàm số trên có 3 cực trị nên nó là đồ thị của hàm số bậc 4. Mà đồ thị hàm số có điểm cực đại nằm trên Oy nên đây là hàm trùng phương.

Đồ thị có 1 cực đại, 2 cực tiểu nên có hệ số a > 0

Câu 23:

Cho hàm số y = f(x) có đồ thị như hình vẽ sau, các khẳng định sau khẳng đinh nào là đúng?

A. Hàm số đạt cực tiểu tại A(-1; -1) và cực đại tại B(1; 3)

B. Hàm số có giá trị cực đại bằng 1

C. Hàm số đạt giá trị nhỏ nhất bằng -1 và đạt giá trị lớn nhất bằng 3

D. Đồ thị hàm số có điểm cực tiểu A(-1; -1) và điểm cực đại B(1; 3).

Xem đáp án

Câu 24:

Đồ thị dưới đây là của hàm số nào?

A. y = x³ – 3x² + 1

B. y = x³ + x² + 1

C. y = -x³ + 3x² + 1

D. y = x³ + x + 1

Xem đáp án

Đáp án D.

Đồ thị hàm số bậc ba y = ax³ + bx² + cx + d có nhánh ngoài cùng bên phải đi lên nên a > 0

Hàm số không có cực trị nên y’ ≥ 0,∀x ∈ R

Câu 25:

Cho hàm số y = 3/(x+1) có đồ thị (C). Mệnh đề nào sau đây là mệnh đề sai?

A. Hàm số không có điểm cực trị

B. Đồ thị (C) không có tiệm cận ngang

C. Đồ thị (C) nhận I(-1; 0) làm tâm đối xứng

D. Hàm số nghịch biến trên mỗi khoảng xác định

Xem đáp án

Đáp án B

Nên đồ thị hàm số có tiệm cận ngang y = 0

Câu 26:

Bảng biến thiên trong hình vẽ dưới đây là bảng biến thiên của hàm số nào?

A. y = -x⁴ + 2x² – 3

B. y = x⁴ – 2x² – 3

C. y = -x⁴ + x² – 3

D. y = x⁴ + 2x² – 3

Xem đáp án

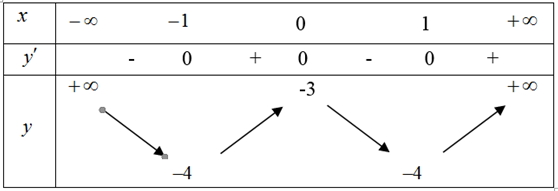
Đáp án B.

Dựa vào BBT ta thấy hàm số có a > 0

Thay x = -1 vào hàm số y = x⁴ – 2x² – 3 ta có y(-1) = (-1)⁴ – 2(-1)² – 3 = -4. Vậy hàm số này thỏa mãn bảng biến thiên bên trên

Câu 27:

Cho hàm số $y = \frac{\sqrt{x^{2} + 1} + x}{3^{x}}$ Khẳng định nào đúng?

A. Hàm số đã cho nghịch biến trên R

B. Hàm số đã cho là hàm số lẻ

C. Giá trị của hàm số đã cho luôn không dương

D. Đồ thị hàm số đã cho có hai tiệm cận ngang

Xem đáp án

Đáp án A

Câu 28:

Hàm số y = x³ – 3x nghịch biến trên khoảng nào?

A. (-∞; 0).

B. (-1;1).

C. (0; +∞).

D. (-∞; +∞).

Xem đáp án

Đáp án B.

Ta có y’ = 3x² – 3; y’ = 0 ó x = ± 1.

Hàm số y = x³ – 3x nghịch biến trên khoảng (-1; 1)

Câu 29:

Cho hàm số $y = \frac{3 x + 1}{2 x - 1}$ . Khẳng định nào sau đây đúng?

A. Đồ thị hàm số có tiệm cận ngang là y = $\frac{3}{2}$

B. Đồ thị hàm số có tiệm cận đứng là x = 1.

C. Đồ thị hàm số không có tiệm cận.

D. Đồ thị hàm số có tiệm cận đứng là y = $\frac{3}{2}$

Xem đáp án

Đáp án :A.

Hàm số là hàm phân thức hữu tỉ bậc nhất và có bậc tử bằng bậc mẫu nên

Đồ thị hàm số có một đường tiệm cận ngang y= $\frac{3}{2}$

. Có

Câu 30:

Cho hàm số y = 1/4.x⁴ – 2x² + 3. Khẳng định nào sau đây đúng?

A. Hàm số nghịch biến trên khoảng (-2; 0) và (2; +∞)

B. Hàm số đồng biến trên khoảng (-∞; -2) và (2; +∞)

C. Hàm số nghịch biến trên khoảng (-∞; -2) và (0; 2)

D. Hàm số nghịch biến trên khoảng (-∞; 0)

Xem đáp án

Đáp án C.

Ta có y = x³ – 4x = x(x² – 4); y’ = 0 <=> x = 0, x = ± 2.

Hàm số nghịch biến trên khoảng (-∞; -2) và (0; 2).

Hàm số đồng biến trên khoảng (-2; 0) và (2; +∞).

Do đó mệnh đề đúng là: Hàm số nghịch biến trên khoảng (-∞; -2) và (0; 2)

CHỌN BỘ SÁCH BẠN MUỐN XEM

250 câu trắc nghiệm Ứng dụng đạo hàm để khảo sát hàm số

250 câu trắc nghiệm Ứng dụng đạo hàm để khảo sát hàm số cơ bản (P8)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương