35 câu hỏi trắc nghiệm thuộc Đề kiểm tra Giữa học kì 2 Toán 12 có đáp án (Mới nhất) (Đề 2)

Câu 1:

Họ nguyên hàm của hàm số

$f (x) = x^{2} - 2 x + 1$ là

A. $F (x) = \frac{1}{3} x^{3} - 2 + x + C$

B. $F (x) = 2 x - 2 + C$

C. $F (x) = \frac{1}{3} x^{3} - x^{2} + x + C$

D. $F (x) = \frac{1}{3} x^{3} - 2 x^{2} + x + C$

Xem đáp án

Chọn C.

$\int f (x) d x = \int (x^{2} - 2 x + 1) d x = \frac{x^{3}}{3} - x^{2} + x + C$

Câu 2:

F(x) là một nguyên hàm của hàm số $f (x) = \frac{2 x + 3}{x^{2}} (x \neq 0)$ ,

biết rằng

$F (1) = 1$ .

$F (x)$ là biểu thức nào sau đây

A. $F (x) = 2 x - \frac{3}{x} + 2$

B. $F (x) = 2 \ln |x| + \frac{3}{x} + 2$

C. $F (x) = 2 x + \frac{3}{x} - 4$

D. $F (x) = 2 \ln |x| - \frac{3}{x} + 4$

Xem đáp án

Chọn D.

$\begin{array}{l} I = \int \frac{2 x + 3}{x^{2}} d x = \int (\frac{2}{x} + \frac{3}{x^{2}}) d x = 2 \ln |x| - \frac{3}{x} + C \\ F (1) = 1 \Rightarrow C = 4 \Rightarrow F (x) = 2 \ln |x| - \frac{3}{x} + 4 \end{array}$

Câu 3:

Nguyên hàm của hàm số $f (x) = \sqrt{x} + 2^{x}$ là

A. $\sqrt{x} + \frac{2^{x}}{\ln 2} + C$

B. $\frac{1}{2 \sqrt{x}} + 2^{x} . \ln 2 + C$

C. $\frac{2}{3} x \sqrt{x} + \frac{2^{x}}{\ln 2} + C$

D. $\frac{3}{2} x \sqrt{x} + 2^{x} . \ln 2 + C$

Xem đáp án

Chọn C.

$\begin{array}{l} \int f (x) d x = \int (\sqrt{x} + 2^{x}) d x = \int x^{\frac{1}{2}} d x + \int 2^{x} d x = \frac{x^{\frac{3}{2}}}{\frac{3}{2}} + \frac{2^{x}}{\ln 2} + C \\ = \frac{2 \sqrt{x^{3}}}{3} + \frac{2^{x}}{\ln 2} + C = \frac{2 x \sqrt{x}}{3} + \frac{2^{x}}{\ln 2} + C \end{array}$

Câu 4:

Một nguyên hàm của hàm số $f (x) = \cos 5 x \cos x$ là:

A. $\cos 6 x$

B. $\sin 6 x$

C. $\frac{1}{2} (\frac{1}{6} \sin 6 x + \frac{1}{4} \sin 4 x)$

D. $- \frac{1}{2} (\frac{\sin 6 x}{6} + \frac{\sin 4 x}{4})$

Xem đáp án

Chọn C.

$I = \int \cos 5 x . \cos x d x = \int \frac{1}{2} (\cos 6 x + \cos 4 x) d x = \frac{1}{2} \int \cos 6 x d x + \frac{1}{2} \int \cos 4 x d x$

$= \frac{1}{12} \sin 6 x + \frac{1}{8} \sin 4 x + C$

Cho C= 0, ta được 1 nguyên hàm của hàm số đã cho là:

$\frac{1}{12} \sin 6 x + \frac{1}{8} \sin 4 x$

$= \frac{1}{2} (\frac{1}{6} \sin 6 x + \frac{1}{4} \sin 4 x)$

Câu 5:

F(x) là một nguyên hàm của hàm số $y = \frac{\ln x}{x}$ . Nếu $F (e^{2}) = 4$ thì $\int \frac{\ln x}{x} d x$ bằng:

A. $F (x) = \frac{\ln^{2} x}{2} + C$

B. $F (x) = \frac{\ln^{2} x}{2} + 2$

C. $F (x) = \frac{\ln^{2} x}{2} - 2$

D. $F (x) = \frac{\ln^{2} x}{2} + x + C$

Xem đáp án

Chọn B.

Đặt

$\ln x = t \Rightarrow d t = \frac{d x}{x}$

Suy ra

$F (x) = \int t d t = \frac{t^{2}}{2} + C = \frac{\ln^{2} x}{2} + C$

Vì

$F (e^{2}) = 4 \Leftrightarrow \frac{\ln^{2} (e^{2})}{2} + C = 4 \Leftrightarrow C = 2$

Câu 6:

Một nguyên hàm của $f (x) = x \ln x$ là kết quả nào sau đây, biết nguyên hàm này triệt tiêu khi x= 1 ?

A. $F (x) = \frac{1}{2} x^{2} \ln x - \frac{1}{4} (x^{2} + 1)$

B. $F (x) = \frac{1}{2} x^{2} \ln x + \frac{1}{4} x + 1$

C. $F (x) = \frac{1}{2} x \ln x + \frac{1}{2} (x^{2} + 1)$

D. Một kết quả khác.

Xem đáp án

Chọn D.

Ta có

$F (x) = \int f (x) d x = \int x \ln x d x$

Đặt

$\{\begin{cases} u = \ln x \\ d v = x d x \end{cases} \Rightarrow \{\begin{cases} d u = \frac{d x}{x} \\ v = \frac{x^{2}}{2} \end{cases}$

Theo công thức tính nguyên hàm từng phần, ta có:

$F (x) = \frac{1}{2} x^{2} \ln x - \frac{1}{2} \int x d x = \frac{1}{2} x^{2} \ln x - \frac{1}{4} x^{2} + C$

Theo bài ra, có:

$F (1) = 0 \Leftrightarrow \frac{1}{2} .1. \ln 1 - \frac{1}{4} {.1}^{2} + C = 0 \Leftrightarrow C = \frac{1}{4}$

Vậy

$F (x) = \frac{1}{2} x^{2} \ln x - \frac{1}{4} x^{2} + \frac{1}{4}$

Câu 7:

Xét hàm số f liên tục trên R và các số thực a, b, c tùy ý. Trong các khẳng định sau, khẳng định nào sai?

A. $\int_{a}^{b} f (x) d x = \int_{c}^{b} f (x) d x - \int_{c}^{a} f (x) d x$

B. $\int_{a}^{b} f (x) d x = \int_{a}^{c} f (x) d x + \int_{c}^{b} f (x) d x$

C. $\int_{a}^{b} f (x) d x = \int_{a}^{c} f (x) d x - \int_{c}^{b} f (x) d x$

D. $\int_{a}^{b} f (x) d x = \int_{a}^{c} f (x) d x - \int_{b}^{c} f (x) d x$

Xem đáp án

Chọn C

Phương án C cần sửa thành:

$\int_{a}^{b} f (x) d x = \int_{a}^{c} f (x) d x + \int_{c}^{b} f (x) d x$

hoặc

$\int_{a}^{b} f (x) d x = \int_{a}^{c} f (x) d x - \int_{b}^{c} f (x) d x$

Câu 8:

Giả sử

$\int_{a}^{b} f (x) d x = 2$ và

$\int_{c}^{b} f (x) d x = 3$ và

$a < b < c$ thì

$\int_{a}^{c} f (x) d x$ bằng bao nhiêu?

A. 5

B. 1

C. -1

D. -5

Xem đáp án

Chọn C.

Ta có

$\int_{a}^{c} f (x) d x = \int_{a}^{b} f (x) d x + \int_{b}^{c} f (x) d x = \int_{a}^{b} f (x) d x - \int_{c}^{b} f (x) d x = 2 - 3 = - 1$

Câu 9:

Tích phân

$I = \int_{0}^{1} {(x + 1)}^{2} d x$ bằng

A. $\frac{8}{3}$

B. 2

C. $\frac{7}{3}$

D. 4

Xem đáp án

Chọn C.

$I = \int_{0}^{1} {(x + 1)}^{2} d x = \int_{0}^{1} (x^{2} + 2 x + 1) d x = {(\frac{x^{3}}{3} + x^{2} + x)|}_{0}^{1} = \frac{7}{3}$

Câu 10:

Tích phân:

$J = \int_{0}^{1} \frac{x d x}{{(x + 1)}^{3}}$ bằng

A. $J = \frac{1}{8}$

B. $J = \frac{1}{4}$

C. $J = 2$

D. $J = 1$

Xem đáp án

Chọn A.

Đặt

$t = x + 1 \Rightarrow d t = d x$ . Đổi cận

$x = 0 \Rightarrow t = 1; x = 1 \Rightarrow t = 2$

$J = \int_{1}^{2} \frac{t - 1}{t^{3}} d t = \int_{1}^{2} (\frac{1}{t^{2}} - \frac{1}{t^{3}}) d t = {(- \frac{1}{t} + \frac{1}{2 t^{2}})|}_{1}^{2} = - \frac{3}{8} + \frac{1}{2} = \frac{1}{8}$

Câu 11:

Giả sử $I = \int_{- 1}^{0} \frac{3 x^{2} + 5 x - 1}{x - 2} d x = a \ln \frac{2}{3} + b$ . Khi đó giá trị a+ 2b là

A. 30

B. 40

C. 50

D. 60

Xem đáp án

Chọn B.

$I = \int_{- 1}^{0} \frac{3 x^{2} + 5 x - 1}{x - 2} d x = \int_{- 1}^{0} (3 x + 11 + \frac{21}{x - 2}) d x$

$= {(\frac{3 x^{2}}{2} + 11 x + 21 \ln |x - 2|)|}_{- 1}^{0} = 21 \ln \frac{2}{3} + \frac{19}{2}$

Suy ra: a = 21;

$b = \frac{19}{2} \Rightarrow a + 2 b = 40$

Câu 12:

Tích phân I = $\int_{0}^{\frac{π}{2}} \sin 3 x . \cos x d x$ có giá trị là:

A. $\frac{1}{2}$

B. $\frac{1}{3}$

C. 1

D. $\frac{1}{4}$

Xem đáp án

Chọn A.

Ta có:

$I = \int_{0}^{\frac{π}{2}} \sin 3 x . \cos x d x = \frac{1}{2} \int_{0}^{\frac{π}{2}} (\sin 4 x + \sin 2 x) d x = \frac{1}{2} {[- \frac{1}{4} \cos 4 x - \frac{1}{2} \cos 2 x]}_{0}^{\frac{π}{2}}$

$= \frac{1}{2} [- \frac{1}{4} (\cos 2 π - \cos 0) - \frac{1}{2} (\cos π - \cos 0)] = \frac{1}{2} [- \frac{1}{4} (1 - 1) - \frac{1}{2} (- 1 - 1)] = \frac{1}{2}$

Câu 13:

Tích phân $I = \int_{- \frac{π}{2}}^{0} \frac{\cos x}{2 + \sin x} d x$ có giá trị là:

A. ln3

B. 0

C. -ln2

D. ln2

Xem đáp án

Chọn D.

Cách 1:

$I = \int_{- \frac{π}{2}}^{0} \frac{\cos x}{2 + \sin x} d x = \int_{- \frac{π}{2}}^{0} \frac{d (2 + \sin x)}{2 + \sin x} = {\ln (2 + \sin x)|}_{- \frac{π}{2}}^{0} = \ln 2$

Vậy

$I = \ln 2$

Cách 2: Đổi biến số đặt

$t = 2 + \sin x$

Câu 14:

Tích phân $I = \int_{0}^{\frac{π}{3}} x \cos x d x$ bằng:

A. $\frac{π \sqrt{3} - 1}{6}$

B. $\frac{π \sqrt{3} - 1}{2}$

C. $\frac{π \sqrt{3}}{6} - \frac{1}{2}$

D. $\frac{π - \sqrt{3}}{2}$

Xem đáp án

Chọn C.

Đặt

$u = x, d u = \cos x d x \Rightarrow d u = d x, v = \sin x$

$\begin{array}{l} I = {[x \sin x]}_{0}^{\frac{π}{3}} - \int_{0}^{\frac{π}{3}} \sin x d x = \frac{π}{3} \sin \frac{π}{3} + {[\cos x]}_{0}^{\frac{π}{3}} \\ = \frac{π}{3} . \frac{\sqrt{3}}{2} + \cos \frac{π}{3} - \cos 0 = \frac{π \sqrt{3}}{6} - \frac{1}{2} \end{array}$

Câu 15:

Tích phân

$I = \int_{1}^{2} \frac{\ln x}{x^{2}} d x$ bằng:

A. $\frac{1}{2} (1 + \ln 2)$

B. $\frac{1}{2} (1 - \ln 2)$

C. $\frac{1}{2} (\ln 2 - 1)$

D. $\frac{1}{4} (1 + \ln 2)$

Xem đáp án

Chọn A.

Đặt $u = \ln x, d v = x^{- 2} d x$ , suy ra $d u = \frac{1}{x} d x, v = - \frac{1}{x}$

$I = \int_{1}^{2} \frac{\ln x}{x^{2}} d x = {- \frac{1}{x} \ln x|}_{1}^{2} + \int_{1}^{2} \frac{1}{x} \cdot \frac{1}{x} d x = {- \frac{1}{x} \ln x|}_{1}^{2} - {\frac{1}{x}|}_{1}^{2} = \frac{1}{2} (1 + \ln 2)$

Câu 16:

Diện tích hình phẳng được giới hạn bởi các đường

$y = x^{3} + 3 x$ ,

$y = - x$ và đường thẳng

$x = - 2$ là:

A. -12 (dvdt)

B. 12 (dvdt)

C. 4 (dvdt)

D. -4 (dvdt)

Xem đáp án

Chọn B.

Phương trình hoành độ giao điểm của hai đồ thị hàm số

$y = x^{3} + 3 x$ và

$y = - x$ là:

$x^{3} + 4 x = 0 \Leftrightarrow x = 0$

Ta có:

$x^{3} + 4 x \leq 0, \forall x \in [- 2; 0]$

Do đó:

$S = \int_{- 2}^{0} |x^{3} + 4 x| d x = - \int_{- 2}^{0} (x^{3} + 4 x) d x = - {(\frac{x^{4}}{4} + 2 x^{2})|}_{- 2}^{0} = 12$

Câu 17:

Cho hàm số f(x) liên tục trên R và $f (x) + f (- x) = \cos^{4} x$ với mọi x $\in$ R. Giá trị của tích phân $I = \int_{\frac{- π}{2}}^{\frac{π}{2}} f (x) d x$ là

A. -2

B. $\frac{3 π}{16}$

C. $\ln 2 - \frac{3}{4}$

D. $\ln 3 - \frac{3}{5}$

Xem đáp án

Chọn B.

Đặt t = - x suy ra: dt = -dx

$\Rightarrow \int_{\frac{- π}{2}}^{\frac{π}{2}} f (x) d x = \int_{\frac{π}{2}}^{- \frac{π}{2}} f (- t) (- d t) = \int_{- \frac{π}{2}}^{\frac{π}{2}} f (- t) d t = \int_{- \frac{π}{2}}^{\frac{π}{2}} f (- x) d x$

$\Rightarrow 2 \int_{\frac{- π}{2}}^{\frac{π}{2}} f (x) d x = \int_{- \frac{π}{2}}^{\frac{π}{2}} [f (x) + f (- x)] d x = \int_{\frac{- π}{2}}^{\frac{π}{2}} \cos^{4} x d x = \frac{3 π}{8}$

$\Rightarrow I = \frac{3 π}{16}$

Câu 18:

Diện tích hình phẳng giới hạn bởi $y = - x, y = 2 x - x^{2}$ có kết quả là

A. 4

B. $\frac{9}{2}$

C. 5

D. $\frac{7}{2}$

Xem đáp án

Chọn B.

Phương trình hoành độ giao điểm của hai đồ thị hàm số

$y = 2 x - x^{2}$ và

$y = - x$ là:

$2 x - x^{2} = - x \Leftrightarrow 3 x - x^{2} = 0 \Leftrightarrow [\begin{array}{l} x = 0 \\ x = 3 \end{array}$

Ta có:

$3 x - x^{2} \geq 0, \forall x \in [0; 3]$

Do đó:

$S = \int_{0}^{3} |3 x - x^{2}| d x = \int_{0}^{3} (3 x - x^{2}) d x = {(\frac{3 x^{2}}{2} - \frac{x^{3}}{3})|}_{0}^{3} = \frac{9}{2}$

Câu 19:

Thể tích của khối tròn xoay được giới hạn bởi đồ thị hàm số $y = f (x)$ liên tục trên đoạn $[a; b]$ trục Ox và hai đường thẳng $x = a, x = b$ quay quanh trục Ox, có công thức là:

A. $V = \int_{a}^{b} f^{2} (x) d x$

B. $V = π \int_{a}^{b} f^{2} (x) d x$

C. $V = π \int_{a}^{b} f (x) d x$

D. $V = π \int_{a}^{b} |f (x)| d x$

Xem đáp án

Chọn B.

Áp dụng công thức tính thể tích khối tròn xoay: giới hạn bởi đồ thị hàm số $y = f (x)$ , trục Ox, x = a, x = b khi quay xung quanh trục Ox ta có: $V = π \int_{a}^{b} f^{2} (x) d x$

Câu 20:

Hình (S) giới hạn bởi $y = 3 x + 2, O x, O y$ . Tính thể tích khối tròn xoay khi quay hình (S) quanh trục Ox.

A. $\frac{8 π}{3}$

B. $\frac{4 π}{3}$

C. $\frac{8 π}{9}$

D. $\frac{16 π}{3}$

Xem đáp án

Chọn C.

Phương trình hoành độ giao điểm:

$3 x + 2 = 0 \Leftrightarrow x = - \frac{2}{3}$

Suy ra:

$V = π \int_{- \frac{2}{3}}^{0} {(3 x + 2)}^{2} d x = π \int_{- \frac{2}{3}}^{0} {(9x}^{2} +12x + 4) d x = π {(3 x^{3} + 6 x^{2} + 4 x)|}_{\frac{- 2}{3}}^{0} = \frac{8 π}{9}$

Câu 21:

Cho hàm số f(x) xác định trên $R \ \{- 1; 1\}$ và thỏa mãn: $f^{'} (x) = \frac{1}{x^{2} - 1}$ . Biết rằng $f (- 3) + f (3) = 0$ và $f (- \frac{1}{2}) + f (\frac{1}{2}) = 2$ . Tính $T = f (- 2) + f (0) + f (4)$

A. $T = 1 + \ln \frac{9}{5}$

B. $T = 1 + \ln \frac{6}{5}$

C. $T = 1 + \frac{1}{2} \ln \frac{9}{5}$

D. $T = 1 + \frac{1}{2} \ln \frac{6}{5}$

Xem đáp án

Chọn C

Ta có $f (x) = \int \frac{1}{x^{2} - 1} d x = \frac{1}{2} \int (\frac{1}{x - 1} - \frac{1}{x + 1}) d x$ $= \frac{1}{2} \ln |\frac{x - 1}{x + 1}| + C$

Với $x \in (- \infty; - 1)$ ; $f (x) = \frac{1}{2} \ln |\frac{x - 1}{x + 1}| + C_{1}$

Với $x \in (1; + \infty)$ ; $f (x) = \frac{1}{2} \ln |\frac{x - 1}{x + 1}| + C_{3}$

Mà $f (- 3) + f (3) = 0$ $\Leftrightarrow \frac{1}{2} \ln |\frac{- 3 - 1}{- 3 + 1}| + C_{1} + \frac{1}{2} \ln |\frac{3 - 1}{3 + 1}| + C_{3} = 0$

$\Leftrightarrow \frac{1}{2} \ln 2 + C_{1} + \frac{1}{2} \ln \frac{1}{2} + C_{3} = 0$ $\Leftrightarrow C_{1} + C_{3} = 0$

Do đó $f (- 2) = \frac{1}{2} \ln 3 + C_{1}$ ; $f (4) = \frac{1}{2} \ln \frac{3}{5} + C_{3}$

Với $x \in (- 1; 1)$ ; $f (x) = \frac{1}{2} \ln |\frac{x - 1}{x + 1}| + C_{2}$

Mà $f (- \frac{1}{2}) + f (\frac{1}{2}) = 2$ $\Leftrightarrow \frac{1}{2} \ln |\frac{- \frac{1}{2} - 1}{- \frac{1}{2} + 1}| + C_{2} + \frac{1}{2} \ln |\frac{\frac{1}{2} - 1}{\frac{1}{2} + 1}| + C_{2} = 2$

$\Leftrightarrow \frac{1}{2} \ln 3 + C_{2} + \frac{1}{2} \ln \frac{1}{3} + C_{2} = 2$ $\Leftrightarrow C_{2} = 1$

Do đó với $x \in (- 1; 1)$ ; $f (x) = \frac{1}{2} \ln |\frac{x - 1}{x + 1}| + 1$ $\Rightarrow f (0) = 1$

Vậy $T = f (- 2) + f (0) + f (4)$ $= 1 + \frac{1}{2} \ln \frac{9}{5}$

Câu 22:

Đồ thị của hàm số $y = f (x)$ trên đoạn [-3;5] như hình vẽ dưới đây(phần cong của đồ thị là một phần của Parabol $y = a x^{2} + b x + c$ ). Tính $I = \int_{- 2}^{3} f (x) d x$

A. $I = \frac{53}{3}$

B. $I = \frac{97}{6}$

C. $I = \frac{43}{2}$

D. $I = \frac{95}{6}$

Xem đáp án

Chọn B

Đồ thị của hàm số y = f(x) trên đoạn [-3;5] như hình vẽ dưới đây (ảnh 2)

Ta có

$I = \int_{- 2}^{3} f (x) d x$ bằng diện tích hình phẳng giới hạn bởi

$Δ_{1}$ ,

$Δ_{2}$ , Parabol

$(P)$ , x=-2, x=3

Với

$Δ_{1}$ qua

$E (- 3; 0)$ ,

$D (0; 4)$ nên có phương trình

$y = \frac{4}{3} x + 4$ ;

$Δ_{2}$ qua

$D (0; 4)$ ;

$C (1; 3)$ nên có phương trình:

$y = - x + 4$ ;

$(P) : y = a x^{2} + b x + c$ qua

$C (1; 3)$ và có đỉnh

$A (2; 4)$ nên

$\{\begin{cases} a + b + c = 3 \\ \frac{- b}{2 a} = 2 \\ 4 a + 2 b + c = 4 \end{cases} \Leftrightarrow \{\begin{cases} a = - 1 \\ b = 4 \\ c = 0 \end{cases} \Rightarrow y = - x^{2} + 4 x$

Vậy

$I = \int_{- 2}^{3} f (x) d x = \int_{- 2}^{0} (\frac{4}{3} x + 4) d x + \int_{0}^{1} (- x + 4) d x + \int_{1}^{3} (- x^{2} + 4 x) d x = \frac{97}{6}$

Câu 23:

Trong không gian với hệ trục tọa độ Oxyz cho A(0;-1;1) , B(-2;1;-1) , C(-1;3;2) . Biết rằng ABCDlà hình bình hành, khi đó tạo độ điểm D là

A. D(-1;-3;-2)

B. D(-1;1; $\frac{2}{3}$ )

C. D(1;3;4)

D. D(1;1;4)

Xem đáp án

Chọn D.

Gọi tọa độ điểm

Ta có

ABCD là hình bình hành

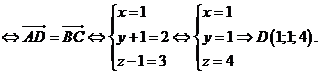
Trong không gian với hệ trục tọa độ Oxyz, cho A( 0;-1;1) (ảnh 3)

Câu 24:

Trong không gian với hệ trục tọa độ Oxyz, cho điểm M(1;-2;5) . Khi đó tọa độ hình chiếu vuông góc M' của M trên mặt phẳng (Oxy) là

A. M'(0;0;5)

B. M'(1;-2;0)

D. M'(1;0;5)

D. M'(0;-2;5)

Xem đáp án

Chọn B.

Ta có M(1;-2;5) , suy ra hình chiếu vuông góc của M trên mặt phẳng (Oxy) là M'(1;-2;0).

Chú ý : Hình chiếu vuông góc của

trên các mặt phẳng

lần lượt là các điểm

Câu 25:

Trong không gian với hệ trục tọa độ Oxyz, cho $(\vec{a}, \vec{b}) = 120 °$ và $|\vec{a}| = 3$ , $|\vec{b}| =$ 4. Khi đó $|\vec{a} - \vec{b}|$ có giá trị bằng bao nhiêu?

A. $|\vec{a} - \vec{b}| = \sqrt{13}$

B. $|\vec{a} - \vec{b}| = \sqrt{37}$

C. $|\vec{a} - \vec{b}| = 1$

D. $|\vec{a} - \vec{b}| = 5$

Xem đáp án

Chọn B.

Ta có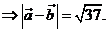

Trong không gian với hệ trục tọa độ Oxyz, cho ( vecto a, vecto b) = 120 độ và (ảnh 2)

Câu 26:

Trong không gian với hệ tọa độ Oxyz, cho hình hộp ABCD.A'B'C'D' có A(-1;0;2) , B(1;1;-1) , D(0;1;1) , A'(2;-1;0) . Thể tích V của khối hình hộp ABCD.A'B'C'D' là

A. V = 1

B. V = 4

C. V = 5

D. V = 6

Xem đáp án

Chọn C

Ta có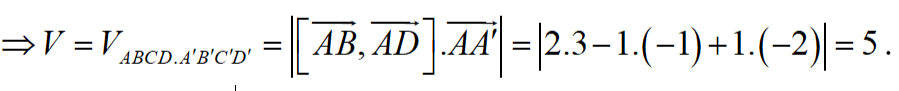

Suy ra

$[\vec{A B}; \vec{A D}] = (2; - 1; 1)$

Trong không gian với hệ tọa độ Oxyz, cho hình hộp ABCD.A'B'C'D' có A(-1;0;2) (ảnh 2)

Câu 27:

Trong không gian với hệ trục tọa độ Oxyz, cho hình hộp ABCD.A'B'C'D' . Biết tọa độ các đỉnh A(-3;2;1) , C(4;2;0) , B'(-2;1;1) , D'(3;5;4) . Tìm tọa độ điểm A' của hình hộp.

A. A'(-3;3;1)

B. A'(-3;-3;3)

C. A'(-3;-3;-3)

D. A'(-3;3;3)

Xem đáp án

Chọn D

Gọi I là trung điểm của AC

$\Rightarrow I (\frac{1}{2}; 2; \frac{1}{2})$

Gọi J là trung điểm của B'D'

$\Rightarrow J (\frac{1}{2}; 3; \frac{5}{2})$

Ta có

$\vec{I J} = (0; 1; 2)$

Ta có

$\vec{A A'} = \vec{I J} \Leftrightarrow \{\begin{cases} x_{A'} + 3 = 0 \\ y_{A'} - 2 = 1 \\ z_{A'} - 1 = 2 \end{cases} \Leftrightarrow \{\begin{cases} x_{A'} = - 3 \\ y_{A'} = 3 \\ z_{A'} = 3 \end{cases}$

Vậy

$A^{'} (- 3; 3; 3)$

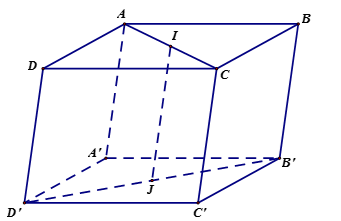
Câu 28:

Trong không gian với hệ tọa độ Oxyz, cho hai điểm . Kí hiệu điểm M thuộc tia đối của tia BA sao cho . Tọa độ của điểm M là

A. Trong không gian với hệ tọa độ Oxyz, cho hai điểm (ảnh 6)

B.

C. (7;6;7)

D. (13;11;5)

Xem đáp án

Chọn C

Gọi . Theo yêu cầu bài toán:

Trong không gian với hệ tọa độ Oxyz, cho hai điểm (ảnh 5)

Câu 29:

Trong không gian với hệ tọa độ Oxyz, cho ba điểm $A (2; - 1; 5), B (5; - 5; 7), M (x; y; 1)$ . Với giá trị nào của x và y thì ba điểm A, B, M thẳng hàng?

A. x=4 và y=7

B. x=-4 và y=-7

C. x=4 và y=-7

D. x=-4 và y=7

Xem đáp án

Chọn D.

Ta có:

$\vec{A M} (x - 2; y + 1; - 4), \vec{A B} (3; - 4; 2)$

Ba điểm A, B, M thẳng hàng khi

$\vec{A M}, \vec{A B}$ cùng phương hay

$\frac{x - 2}{3} = \frac{y + 1}{- 4} = - 2 \Rightarrow \{\begin{cases} x = - 4 \\ y = 7 \end{cases}$

Câu 30:

Cho 2 vectơ

$\vec{a} = (2; - \sqrt{3}; 1), \vec{b} = (\sin 3 x; sinx; c o s x)$ .

$\vec{a} ⊥ \vec{b}$ khi:

A. $x = - \frac{π}{24} + \frac{k π}{4} \lor x = \frac{2 π}{3} + k π, (k \in Z)$

B. $x = \frac{7 π}{24} + \frac{k π}{2} \lor x = - \frac{π}{12} + k π, (k \in Z)$

C. $x = \frac{π}{24} + \frac{k π}{2} \lor x = - \frac{π}{12} + k π, (k \in Z)$

D. $x = \frac{7 π}{24} + \frac{k π}{2} \lor x = \frac{π}{12} + k π, (k \in Z)$

Xem đáp án

Chọn B

$\vec{a} ⊥ \vec{b}$ khi

$\vec{a} . \vec{b} = 0$

$\Leftrightarrow 2 \sin 3 x - \sqrt{3} sinx + c o s x = 0$

$\Leftrightarrow \sin 3 x = \frac{\sqrt{3}}{2} sinx - \frac{1}{2} \cos x$

$\Leftrightarrow \sin 3 x = \sin (x - \frac{π}{6})$

$\Leftrightarrow [\begin{array}{l} 3 x = x - \frac{π}{6} + k 2 π \\ 3 x = π - x + \frac{π}{6} + k 2 π \end{array} \Leftrightarrow [\begin{array}{l} x = - \frac{π}{12} + k π \\ x = \frac{7 π}{24} + \frac{k π}{2} \end{array}, k \in Z$

Câu 31:

Cho hai vectơ $\vec{a} = (1; 1; - 2), \vec{b} = (1; 0; m)$ . Góc giữa chúng bằng $45^{0}$ khi:

A. $m = 2 + \sqrt{6}$

B. $m = 2 - \sqrt{6}$

C. $m = 2 \pm \sqrt{6}$

D. $m = 2 \sqrt{6}$

Xem đáp án

Chọn B.

$\cos (\vec{u}, \vec{v}) = \frac{\vec{u} . \vec{v}}{|\vec{u}| . |\vec{v}|} = \frac{1 - 2 m}{\sqrt{6} \sqrt{m^{2} + 1}}$

Góc giữa hai vecto

$\vec{a}, \vec{b}$ có số đo

$45^{0}$ nên ta có:

$\frac{1 - 2 m}{\sqrt{6} \sqrt{m^{2} + 1}} = c {os45}^{0} = \frac{1}{\sqrt{2}} \Leftrightarrow 1 - 2 m = \sqrt{3} \sqrt{m^{2} + 1}$

$\Leftrightarrow \{\begin{cases} 1 - 2 m \geq 0 \\ {(1 - 2 m)}^{2} = 3 (m^{2} + 1) \end{cases}$

$\Leftrightarrow \{\begin{cases} m \leq \frac{1}{2} \\ m^{2} - 4 m - 2 = 0 \end{cases} \Leftrightarrow \{\begin{cases} m \leq \frac{1}{2} \\ [\begin{array}{l} m = 2 - \sqrt{6} \\ m = 2 + \sqrt{6} \end{array} \end{cases} \Leftrightarrow m = 2 - \sqrt{6}$

Câu 32:

Trong không gian với hệ toạ độ Oxyz, cho ba điểm $A (2; - 3; 4), B (1; y; - 1) C (x; 4; 3)$ . Để ba điểm A, B, C thẳng hàng thì tổng giá trị 5x + y là:

A. 41

B. 40

C. 42

D. 36

Xem đáp án

Chọn A.

Có

$\vec{A B} = (- 1; y + 3; - 5); \vec{A C} = (x - 2; 7; - 1)$

Để ba điểm A, B, C thẳng hàng thì

$\vec{A B}$ cùng phương

$\vec{A C}$

$\Leftrightarrow \frac{- 1}{x - 2} = \frac{y + 3}{7} = \frac{- 5}{- 1}$

$\Rightarrow x = \frac{9}{5}; y = 32$

$\Rightarrow 5x+y=41$

Vậy

$5x+y=41$

Câu 33:

Ba vectơ đồng phẳng khi:

A. $[\begin{array}{l} m = 9 \\ m = 1 \end{array}$

B. $[\begin{array}{l} m = - 9 \\ m = 1 \end{array}$

C. $[\begin{array}{l} m = 9 \\ m = - 2 \end{array}$

D. $[\begin{array}{l} m = - 9 \\ m = - 1 \end{array}$

Xem đáp án

Chọn A.

Ta có:

$[\vec{a}, \vec{b}] = (2 m - 3; 6 - m; - 3)$

Ba vectơ

$\vec{a}, \vec{b}, \vec{c}$ đồng phẳng khi

$[\vec{a}, \vec{b}] \vec{c} = 0$

$\begin{array}{l} \Leftrightarrow 2. (2 m - 3) + m . (6 - m) + 1. (- 3) = 0 \\ \Leftrightarrow 4 m - 6 + 6 m - m^{2} - 3 = 0 \end{array}$

$\Leftrightarrow m^{2} - 10 m + 9 = 0$

$\Leftrightarrow [\begin{array}{l} m = 9 \\ m = 1 \end{array}$

Câu 34:

Trong không gian với hệ trục tọa độ Oxyz, cho tam giác ABC với $A (1; 2; 1),$ $B (2; 1; 3),$ $C (3; 2; 2)$ . Diện tích tam giác ABC bằng

A. $\frac{\sqrt{11}}{2}$

B. $\sqrt{3}$

C. $\frac{\sqrt{13}}{2}$

D. $\frac{\sqrt{14}}{2}$

Xem đáp án

Chọn D

+

$\{\begin{cases} \vec{A B} = (1; - 1; 2) \\ \vec{A C} = (2; 0; 1) \end{cases} \Rightarrow [\vec{A B}, \vec{A C}] = (- 1; 3; 2)$

$\Rightarrow |[\vec{A B}, \vec{A C}]| = \sqrt{14}$

+

$S_{Δ A B C} = \frac{1}{2} |[\vec{A B}, \vec{A C}]| = \frac{\sqrt{14}}{2}$

Câu 35:

Trong không gian với hệ trục tọa độ Oxyz, cho tứ diện ABCD với $A (1; 2; 1),$ $B (2; 1; 3),$ $C (3; 2; 2),$ $D (1; 1; 1)$ . Thể tích của tứ diện ABCD bằng

A. 1

B. 2

C. $\frac{1}{2}$

D. 3

Xem đáp án

Chọn C.

+

$\{\begin{cases} \vec{A B} = (1; - 1; 2) \\ \vec{A C} = (2; 0; 1) \end{cases} \Rightarrow [\vec{A B}, \vec{A C}] = (- 1; 3; 2)$

$\vec{A D} = (0; - 1; 0)$

+

$[\vec{A B}, \vec{A C}] . \vec{A D} = - 3$

$\Rightarrow V_{A B C D} = \frac{1}{6} |[\vec{A B}, \vec{A C}] . \vec{A D}| = \frac{1}{2}$

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đề kiểm tra Giữa học kì 2 Toán 12 có đáp án (Mới nhất)

Đề kiểm tra Giữa học kì 2 Toán 12 có đáp án (Mới nhất) (Đề 2)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương