31 câu hỏi trắc nghiệm thuộc Đề kiểm tra Giữa học kì 2 Toán 12 có đáp án (Mới nhất) (Đề 11)

Câu 1:

Trong không gian Oxyz, gọi A' là điểm đối xứng với A (3; 5; −7) qua trục Oz. Hãy tìm tọa độ điểm A'

A. A' (−3; −5; −7).

B. A' (3; 5; 7).

C. A' (0; 0; −7).V

D. A' (3; 5; 0).

Xem đáp án

Đáp án đúng là A

Gọi M là hình chiếu của điểm A trên trục Oz

M là hình chiếu của điểm A trên trục Oz nên tọa độ của điểm M (0; 0; −7)

Vì A' đối xứng với A qua Oz nên M là trung điểm của AA'

Do đó ta có:

x_M = $\frac{x_{A} + x_{A'}}{2} = \frac{3 + x_{A'}}{2}$ = 0

y_M = $\frac{y_{A} + y_{A'}}{2} = \frac{5 + y_{A'}}{2}$ = 0

z_M = $\frac{z_{A} + z_{A'}}{2} = \frac{- 7 + z_{A'}}{2}$ = −7

Vậy Điểm A' có tọa độ là A' (−3; −5; −7).

Câu 2:

Trong không gian với hệ tọa độ Oxyz, phương trình nào dưới đây là phương trình mặt phẳng đi qua gốc tọa độ O?

A. 2y + 3z + 1 = 0.

B. 2x + 3z = 0.

C. 2x + 3 = 0.

D. −2x + y + 1 = 0.

Xem đáp án

Đáp án đúng là B

Thay điểm O (0; 0; 0) vào phương trình 2y + 3z + 1 = 0, ta được:

2.0 + 3.0 + 1 ≠ 0.

Do đó phương trình mặt phẳng 2y + 3z + 1 = 0 không đi qua gốc tọa độ O.

Thay điểm O (0; 0; 0) vào phương trình 2x + 3z = 0, ta được:

2.0 + 3.0 = 0.

Do đó phương trình mặt phẳng 2x + 3z = 0 đi qua gốc tọa độ O.

Thay điểm O (0; 0; 0) vào phương trình 2x + 3 = 0, ta được:

2.0 + 3 = 3 ≠ 0.

Do đó phương trình mặt phẳng 2x + 3 = 0 không đi qua gốc tọa độ O.

Thay điểm O (0; 0; 0) vào phương trình −2x + y + 1 = 0, ta được:

−2.0 + 0 + 1 = 1 ≠ 0.

Do đó phương trình mặt phẳng −2x + y + 1 = 0 không đi qua gốc tọa độ O.

Vậy chọn đáp án B.

Câu 3:

Khẳng định nào dưới đây là khẳng định đúng?

A.

\int 3 x^{2} dx

= 9x³ + C.

B.

\int 3 x^{2} dx

= x³ + C.

C.

\int 3 x^{2} dx

=

\frac{3}{2}

x + C.

D.

\int 3 x^{2} dx

= 6x + C.

Xem đáp án

Đáp án đúng là B

Ta có công thức tính nguyên hàm là: $\int {ax}^{n} dx$ = $\frac{a . x^{n + 1}}{n + 1}$ + C

Vậy nên $\int 3 x^{2} dx$ = x³ + C.

Câu 4:

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có phương trình (x + 2)² + (y − 1)² + z² = 4. Hãy tìm tọa độ tâm I và bán kính R của mặt cầu

A. I (2; −1; 0), R = 4.

B. I (−2; 1; 0), R = 4.

C. I (2; −1; 0), R = 2

D. I (−2; 1; 0), R = 2.

Xem đáp án

Đáp án đúng là D

Ta có: Phương trình tổng quát của mặt cầu tâm I (a; b; c) có bán kính R là

(x – a )² + (y – b)²+ (z – c)² = R²

Do đó tâm I và bán kính R của mặt cầu (S): (x + 2)² + (y − 1)² + z² = 4 lần lượt là I (−2; 1; 0) và R = 2.

Câu 5:

Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P) có phương trình x – 3z + 5 = 0. Hãy tìm tọa độ một vectơ pháp tuyến $\vec{n}$ của (P)

A.

\vec{n}

= (1; 0; –3).

B.

\vec{n}

= (1; –3; 5).

C.

\vec{n}

= (1; –3; 0).

D.

\vec{n}

= (0; –3; 5).

Xem đáp án

Đáp án đúng là A

Trong không gian Oxyz, phương trình mặt phẳng có VTPT $\vec{n}$ = (a; b; c) có dạng là ax + by + cz + d = 0.

Do đó tọa độ một vectơ pháp tuyến của (P): x – 3z + 5 = 0 là $\vec{n}$ = (1; 0; –3).

Câu 6:

Nếu $\int_{0}^{1} f (x) dx$ = 4 thì $\int_{0}^{1} 2 . f (x) dx$ bằng

A. 16

B. 4

C. 8

D. 2

Xem đáp án

Đáp án đúng là C

$\int_{1}^{2} 2 f (x) dx$ = 2. $\int_{1}^{2} f (x) dx$ = 2. 4 = 8.

Câu 7:

Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng (P): 2x – y + 3z – 4 = 0 và (Q): 4x – 2y + 6z – 4 = 0. Hãy tìm mệnh đề đúng trong các mệnh đề sau

A. (P) // (Q).

B. (P) ⋂ (Q) = d.

C. (P) ≡ (Q).

D. (P) ⊥ (Q).

Xem đáp án

Đáp án đúng là A

Xét hai mặt phẳng (P): 2x – y + 3z – 4 = 0 và (Q): 4x – 2y + 6z – 4 = 0, ta có :

$\frac{2}{4} = \frac{- 1}{- 2} = \frac{3}{6} \neq \frac{4}{4}$

Do đó (P) và (Q) song song với nhau

Câu 8:

Trong không gian với hệ tọa độ Oxyz, hãy tìm tọa độ trung điểm I của đoạn AB, biết A (2; –3; 0), B (2; 3; 2)

A. I (0; 3; 2).

B. I (–2; 0; –1).

C. I (2; 0; 1).

D. I (0; –3; –2).

Xem đáp án

Đáp án đúng là C

Ta có: x_I = $\frac{x_{A} + x_{B}}{2} = \frac{2 + 2}{2}$ = 2

y_I= $\frac{y_{A} + y_{B}}{2} = \frac{- 3 + 3}{2}$ = 0

z_I = $\frac{z_{A} + z_{B}}{2} = \frac{0 + 2}{2}$ = 1

Vậy tọa độ trung điểm I là I (2; 0; 1).

Câu 9:

Trong không gian với hệ tọa độ Oxyz, gọi điểm H là hình chiếu vuông góc của điểm A (3; 5; –7) lên trục Oz. Hãy tìm tọa độ của điểm H

A. H (0; 0; –7).

B. H (3; 5; 0).

C. H (0; 0; 7).

D. H (–3; –5; 0).

Xem đáp án

Đáp án đúng là A

Vì H là hình chiếu vuông góc của điểm A (3; 5; –7) lên trên trục Oz nên x = 0, y = 0 và z = –7

Vậy tọa độ điểm H là H (0; 0; –7).

Câu 10:

Hãy tìm họ nguyên hàm F(x) của hàm số f (x) = 3^x +

\frac{1}{s {in}^{2} x}

A. F(x) =

\frac{3^{x}}{\ln 3}

+ cotx + C.

B. F(x) = 3^x.ln3 + cotx + C.

C. F(x) =

\frac{3^{x}}{\ln 3}

– cotx + C.

D. F(x) = 3^x.ln3 – cotx + C.

Xem đáp án

Đáp án đúng là A

$\int (3^{x} + \frac{1}{s {in}^{2} x}) dx = \int 3^{x} dx + \int \frac{1}{s {in}^{2} x} dx$

= $\frac{3^{x}}{\ln 3}$ + cotx + C.

Câu 11:

Họ các nguyên hàm F(x) của hàm số f (x) = 5^x – x là

A. F(x) = 5^x.ln2 –

\frac{x^{2}}{2}

+ C.

B. F(x) = 5^x – x² + C.

C. F(x) =

\frac{5^{x}}{\ln 5}

– 1+ C.

D. F(x) =

\frac{5^{x}}{\ln 5} - \frac{x^{2}}{2}

+ C.

Xem đáp án

Đáp án đúng là D

$\begin{array}{l} \int (5^{x} - x) dx = \int 5^{x} dx - \int xdx \\ = \frac{5^{x}}{\ln 5} - \frac{x^{2}}{2} + C \end{array}$

Câu 12:

Cho hai hàm số f (x) và g (x) liên tục trên đoạn [a; b] và số thực c thỏa mãn a < c < b. Khẳng định nào sau đây là sai?

A.

\int_{a}^{b} k . f (x) d x = k \int_{a}^{b} f (x) d x

(k là hằng số khác 0).

B.

\int_{a}^{b} f (x) g (x) d x = \int_{a}^{b} f (x) d x . \int_{a}^{b} g (x) d x

C. $\int_{a}^{b} [f (x) + g (x)] d x = \int_{a}^{b} f (x) d x + \int_{a}^{b} g (x) d x$

D. $\int_{a}^{b} f (x) d x = \int_{a}^{c} f (x) d x + \int_{c}^{b} f (x) d x$

Xem đáp án

Đáp án đúng là B

Theo tính chất của tích phân:

$\int_{a}^{b} k . f (x) d x = k \int_{a}^{b} f (x) d x$ ( k là hằng số khác 0). Do đó đáp án A đúng.

$\int_{a}^{b} [f (x) + g (x)] d x = \int_{a}^{b} f (x) d x + \int_{a}^{b} g (x) d x$ . Do đó đáp án C đúng, B sai.

$\int_{a}^{b} f (x) d x = \int_{a}^{c} f (x) d x + \int_{c}^{b} f (x) d x$ . Do đó đáp án D đúng.

Câu 13:

Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): 2x – y + 3z – 4 = 0. Trong các điểm sau, điểm nào thuộc mặt phẳng (P)?

A. Q (0; –3; 5).

B. N (1; –3; 5).

C. P (1; –3; 0).

D. M (0; –4; 0).

Xem đáp án

Đáp án đúng là D

Thay tọa độ các điểm vào phương trình mặt phẳng (P) ta được:

+ Thay tọa độ điểm Q (0; –3; 5) vào phương trình mặt phẳng ta được:

2x – y + 3z – 4 = 0

2.0 – (–3) + 3.5 – 4 = 0

14 = 0 (vô lý)

Vậy nên điểm Q không thuộc mặt phẳng (P)

+ Thay tọa độ điểm N (1; –3; 5) vào phương trình mặt phẳng ta được

2x – y + 3z – 4 = 0

2.1 – (–3) + 3.5 – 4 = 0

16 = 0 (vô lý)

Vậy nên điểm N không thuộc mặt phẳng (P)

+ Thay tọa độ điểm P (1; –3; 0) vào phương trình mặt phẳng ta được:

2x – y + 3z – 4 = 0

2.1 – (–3) + 3.0 – 4 = 0

1 = 0 (vô lý)

Vậy nên điểm P không thuộc mặt phẳng (P)

+ Thay tọa độ điểm M (0; –4; 0) vào phương trình mặt phẳng ta được:

2x – y + 3z – 4 = 0

2.0 – (–4) + 3.0 – 4 = 0

0 = 0 (đúng)

Vậy nên điểm M thuộc mặt phẳng (P)

Do đó chọn đáp án D, điểm thuộc mặt phẳng (P) là điểm M (0; –4; 0).

Câu 14:

Trong không gian với hệ tọa độ Oxyz, cho vectơ

\vec{a}

thỏa mãn hệ thức

\vec{a}

= –2

\vec{j}

+ 3

\vec{k}

. Bộ số nào dưới đây là tọa độ của vectơ

\vec{a}

A. (–2; 3; 0).

B. (0; –2; 3).

C. (–2; 0; 3).

D. (0; 3; –2).

Xem đáp án

Đáp án đúng là B

Trên mỗi trục tọa độ người ta quy ước các vectơ đơn vị $\vec{i}, \vec{j}, \vec{k}$ .Tất cả các vectơ trong không gian đều được biểu diễn qua các vectơ đơn vị.

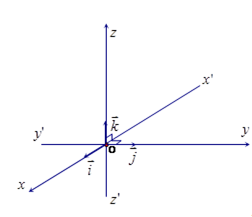
Trong không gian với hệ tọa độ Oxyz, cho vectơ a thỏa mãn hệ thức vecto a= –2 vecto j + 3 vecto k . (ảnh 1)

Vậy nên tọa độ vectơ

\vec{a}

là (0; –2; 3).

Câu 15:

Cho hàm số g (x) xác định trên K và G (x) là một nguyên hàm của g (x) trên K. Khẳng định nào dưới đây đúng?

A. G (x) = g (x), ∀ x Î K.

B. g'(x) = G (x), ∀ x Î K.

C. G'(x) = g (x), ∀ x Î K.

D. G'(x) = g'(x), ∀ x Î K.

Xem đáp án

Đáp án đúng là C

Vì G (x) là nguyên hàm của g (x) nên đạo hàm của G(x) sẽ bằng g(x): G'(x) = g (x).

Do đó khẳng định đúng là C.

Câu 16:

Trong không gian với hệ tọa độ Oxyz, cho vectơ

\vec{a}

= (–2; 3; 1). Hãy tính độ dài của vectơ

\vec{a}

A. $|\vec{a}| = 2$

B. $|\vec{a}| = \sqrt{2}$

C. $|\vec{a}| = \sqrt{6}$

D. $|\vec{a}| = \sqrt{14}$

Xem đáp án

Đáp án đúng là D

Độ dài của vectơ $\vec{a}$ là:

$|\vec{a}| = \sqrt{{(- 2)}^{2} + 3^{2} + 1^{2}} = \sqrt{14}$

Câu 17:

Trong không gian với hệ tọa độ Oxyz, cho hai điểm A (–1; 2; 1), B (2; 1; 0). Mặt phẳng qua A và vuông góc với đường thẳng AB có phương trình là

A. 3x – y – z – 6 = 0.

B. x + 3y + z – 5 = 0.

C. 3x – y – z + 6 = 0.

D. x + 3y + z – 6 = 0.

Xem đáp án

Đáp án đúng là C

Gọi mặt phẳng qua A và vuông góc với đường thẳng AB là mặt phẳng (P).

Vì mặt phẳng (P) vuông góc với đường thẳng AB nên VTPT của mặt phẳng (P) là $\vec{AB}$ = (3; –1; –1).

Do đó phương trình mặt phẳng (P) có dạng là 3x – y – z + d = 0 (1)

Vì mặt phẳng (P) đi qua điểm A (–1; 2; 1) nên thay tọa độ điểm A vào (1) ta được:

3.(–1) – 2 – 1 + d = 0 => d = 6

Vậy mặt phẳng đi qua A và vuông góc với đường thẳng AB có phương trình là:

3x – y – z + 6 = 0.

Câu 18:

Cho

\int_{0}^{5} f (x) d x

= –2. Tích phân

\int_{0}^{5} [4 f (x) - 2 x] d x

bằng

A. -33

B. 33

C. 6

D. -10

Xem đáp án

Đáp án đúng là A

Ta có: $\int_{0}^{5} [4 f (x) - 2 x] d x = 4. \int_{0}^{5} f (x) d x - \int_{0}^{5} 2 x dx$

= 4. (–2) – 25 = –33.

Câu 19:

Nếu các số hữu tỉ a, b thỏa mãn

\int_{0}^{1} (a e^{x} + b) d x

= e + 2 thì giá trị của biểu thức a + b bằng

A. 6

B. 3

C. 5

D. 4

Xem đáp án

Đáp án đúng là D

Ta có: $\int_{0}^{1} (a e^{x} + b) d x = \int_{0}^{1} {ae}^{x} dx + \int_{0}^{1} bdx$

= ${(a . e^{x})|}_{0}^{1} + {(b . x)|}_{0}^{1}$ = ae – a + b.

Theo giả thiết thì: $\int_{0}^{1} (a e^{x} + b) d x$ = e + 2.

Khi đó $\int_{0}^{1} (a e^{x} + b) d x$ = ae – a + b = e + 2.

Do đó a = 1, b = 3.

Vậy a + b = 1 + 3 = 4.

Câu 20:

Hãy tìm họ nguyên hàm F (x) của hàm số f (x) = e^{5x + 3}+ (2x + 1)²⁰²²

A. F (x) =

\frac{1}{5}

e^{5x + 3}+

\frac{{(2 x + 1)}^{2023}}{2023}

+ C.

B. F (x) = e^{5x + 3}+

\frac{1}{2}

.

\frac{{(2 x + 1)}^{2023}}{2023}

+ C.

C. F (x) = e^{5x + 3}+

\frac{{(2 x + 1)}^{2023}}{2023}

+ C.

D. F (x) =

\frac{1}{5}

e^{5x + 3}+

\frac{1}{2}

.

\frac{{(2 x + 1)}^{2023}}{2023}

+ C.

Xem đáp án

Đáp án đúng là D

Ta có công thức:

\int e^{ax + b} d x = \frac{1}{a} . e^{ax + b} + C

\int {(ax + b)}^{n} d x = \frac{1}{a . (n + 1)} . {(ax + b)}^{n + 1} + C

Do đó:

$\begin{array}{l} \int [e^{5 x + 3} + {(2 x + 1)}^{2022}] d x \\ = \int e^{5 x + 3} d x + \int {(2 x + 1)}^{2022} d x \\ = \frac{1}{5} e^{5 x + 3} + \frac{1}{2} . \frac{{(2 x + 1)}^{2023}}{2023} + C \end{array}$

Câu 21:

Trong không gian Oxyz, cho A (0; –1; 1), B (–2; 1; –1), C (–1; 3; 2). Biết rằng ABCD là hình bình hành, khi đó tọa độ điểm D là

A. D (1; 1; 4).

B. D (1; 3; 4).

C. D

(- 1; 1; \frac{2}{3})

.

D. D (–1; –3; –2).

Xem đáp án

Đáp án đúng là A

Vì ABCD là hình bình hành nên:

x_D = 2. $\frac{x_{A} + x_{C} - x_{B}}{2}$ = 2. $\frac{0 - 1 + 2}{2}$ . Do đó x_D= 1.

y_D = 2. $\frac{y_{A} + y_{C} - y_{B}}{2}$ = 2. $\frac{- 1 + 3 - 1}{2}$ . Do đó y_D = 1.

z_D = 2. $\frac{z_{A} + z_{C} - z_{B}}{2}$ = 2. $\frac{1 + 2 + 1}{2}$ . Do đó z_D = 4.

Vậy tọa độ điểm D là D (1; 1; 4).

Câu 22:

Cho biết

\int_{1}^{e} \frac{1 + x}{x^{2}} d x

= a +

\frac{b}{e}

, với a, b Î ℝ. Giá trị a.b bằng

A. 1

B. -1

C. -2

D. 2

Xem đáp án

Đáp án đúng là C

$\begin{array}{l} \int_{1}^{e} \frac{1 + x}{x^{2}} d x= \int_{1}^{e} \frac{1}{x^{2}} d x + \int_{1}^{e} \frac{1}{x} d x \\ = {(\frac{- 1}{x})|}_{1}^{e} + {\ln x|}_{1}^{e} \end{array}$

= – $\frac{1}{e}$ + 1 + 1 = 2 – $\frac{1}{e}$ .

Do đó a = 2, b = –1.

Vậy a.b = 2. (–1) = –2.

Câu 23:

Tìm tất cả các giá trị của tham số m để hàm số F (x) = m²x³ + (3m + 2) x²– 4x + 3 là một nguyên hàm của hàm số f (x) = 3x²+ 10x – 4.

A. m = 2.

B. m = 1.

C. m = ±1.

D. m = ±2.

Xem đáp án

Đáp án đúng là B

Ta có $\int (3 x^{2} + 10 x - 4) d x$ = x³ + 5x² – 4 + C.

Vì F (x) = m²x³ + (3m + 2) x²– 4x + 3 là một nguyên hàm của f (x) nên:

x³ + 5x² – 4 + C = m²x³ + (3m + 2) x²– 4x + 3

Do đó m² = 1 và 3m + 2 = 5.

Giải hệ phương trình $\{\begin{cases} m^{2} = 1 \\ 3 m + 2 = 5 \end{cases}$ ta tìm được m = 1 thỏa mãn yêu cầu đầu bài.

Câu 24:

Trong không gian Oxyz, mặt cầu có tâm I (–1; 2; –3) và đi qua điểm A (2; 0; 0) có phương trình là

A. (x + 1)² + (y – 2)² + (z + 3)² = 11.

B. (x + 1)² + (y – 2)² + (z + 3)² = 22.

C. (x – 1)² + (y + 2)² + (z – 3)² = 22.

D. (x – 1)² + (y – 2)² + (z – 3)² = 2.

Xem đáp án

Đáp án đúng là B

Mặt cầu có tâm I (–1; 2; –3) nên phương trình mặt cầu có dạng là:

(x + 1)² + (y – 2)² + (z + 3)² = R² (1)

Vì mặt cầu đi qua điểm A (2; 0; 0) nên thay tọa độ điểm A vào (1) ta được:

(2 + 1)² + (0 – 2)² + (0 + 3)² = R² => R²= 22

Vậy phương trình mặt cầu là: (x + 1)² + (y – 2)² + (z + 3)² = 22.

Câu 25:

Trong không gian Oxyz, mặt phẳng đi qua điểm A (2; –1; 2) và song song với mặt phẳng (P): 2x – y + 3z + 2 = 0 có phương trình là

A. 2x – y + 3z – 9 = 0.

B. 2x – y + 3z + 11 = 0.

C. 2x – y + 3z – 11 = 0.

D. 2x – y – 3z + 11 = 0.

Xem đáp án

Đáp án đúng là C

Phương trình mặt phẳng song song với mặt phẳng (P) nên có dạng:

2x – y + 3z + d = 0 (1)

Mặt phẳng đó đi qua điểm A (2; –1; 2) nên thay tọa độ điểm A vào (1) ta được:

2.2 – (–1) + 3.2 + d = 0 => d = –11

Vậy phương trình mặt phẳng cần tìm là: 2x – y + 3z – 11 = 0.

Câu 26:

Hãy tìm một nguyên hàm F (x) của hàm số f (x) =

\frac{1}{co s^{2} x}

, biết F

(\frac{π}{4})

= 3.

A. F (x) = tanx + C.

B. F (x) = tanx + 2.

C. F (x) = tanx + 4.

D. F (x) = tanx + 3.

Xem đáp án

Đáp án đúng là B

Ta có: F(x) = $\int \frac{1}{\cos^{2} x} d x$ = tanx + C

Theo đầu bài thì F $(\frac{π}{4})$ = 3 do đó

tan $(\frac{π}{4})$ + C = 3 => C = 2

Vậy F(x) = tanx + 2.

Câu 27:

Trong không gian Oxyz, khoảng cách từ A (2; 0; 1) đến mặt phẳng (P): 2x + y – 2z + 6 = 0 bằng

A. $\frac{8}{3}$

B. $\frac{2}{3}$

C. $\frac{8}{9}$

D. $\frac{2}{9}$

Xem đáp án

Đáp án đúng là A

Ta có công thức tính khoảng cách từ một điểm M (x₀; y₀; z₀) đến một mặt phẳng ax + by + cz + d = 0 là: $\frac{|{ax}_{0} + {by}_{0} + {cz}_{0} + d|}{\sqrt{a^{2} + b^{2} + c^{2}}}$ .

Áp dụng công thức trên ta tính được khoảng cách từ A (2; 0; 1) đến mặt phẳng (P): 2x + y – 2z + 6 = 0 là:

d(A, (P)) =

\frac{|2.2 + 0.1 + 1. (- 2) + 6|}{\sqrt{2^{2} + 1^{2} + {(- 2)}^{2}}} = \frac{8}{3}

Câu 28:

Trong không gian Oxyz, cho ba điểm M (3; 2; 8), N (0; 1; 3) và P (2; m; 4). Tìm giá trị m sao cho tam giác MPN vuông tại N

A. m = 4.

B. m = –1.

C. m = 25.

D. m = –10.

Xem đáp án

Đáp án đúng là D

Ta có: $\vec{NP}$ = (2; m – 1; 1), $\vec{MN}$ = (–3; –1; –5)

Vì tam giác MNP vuông tại N nên $\vec{MN} . \vec{NP}$ = 0

2. (–3) + (m – 1). (–1) + 1. (–5) = 0

–m – 10 = 0

m = – 10.

Câu 29:

Tính I =

\int_{0}^{\frac{π}{2}} xs inx d x

.

Xem đáp án

Đặt u = x => du = dx

dv = sinxdx => v = – cosx + C

Chọn C = 0 => v = – cosx

=> I = $\int_{0}^{\frac{π}{2}} xs inx d x = {- x . co sx|}_{0}^{\frac{π}{2}} + \int_{0}^{\frac{π}{2}} co sxdx$

= – $\frac{π}{2}$ .cos $(\frac{π}{2})$ +0. cos (0) + ${s inx|}_{0}^{\frac{π}{2}}$

= sin $(\frac{π}{2})$ – sin (0) = 1.

Câu 30:

Trong không gian Oxyz, viết phương trình mặt phẳng (P) đi qua hai điểm A (1; 2; 0), B (2; 3; 1) và song song với Oz.

Xem đáp án

Ta có: $\vec{AB}$ = (1; 1; 1), $\vec{u_{Oz}}$ = (0; 0; 1).

Vì phương trình mặt phẳng song song với trục Oz và đi qua hai điểm A, B nên VTPT của mặt phẳng đó là: $\vec{n}$ = $[\vec{AB}, \vec{u_{Oz}}]$ = (1.1 – 1.0; 1.0 – 1.1; 1.0 – 1.0).