Đề kiểm tra Giữa học kì 2 Toán 12 có đáp án (Mới nhất) (Đề 4)
-
1573 lượt thi
-
35 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 3:
Chọn D.
Đặt t = sin x, suy ra dt = cosx.dx.
Khi đóCâu 4:
Chọn B.
Chú ý: “ Nhất log, nhì đa, tam lượng, tứ mũ”.Câu 7:
Câu 8:
Chọn C.
Áp dụng công thức tích phân từng phần, ta có
Câu 18:
Chọn A.
Ta có (1)
Tính .
Đặt
.
Thay vào (1), ta đượcCâu 19:
Chọn A.
Phương trình hoành độ giao điểm của hai đồ thị hàm số và trục y=1 là:
Câu 20:
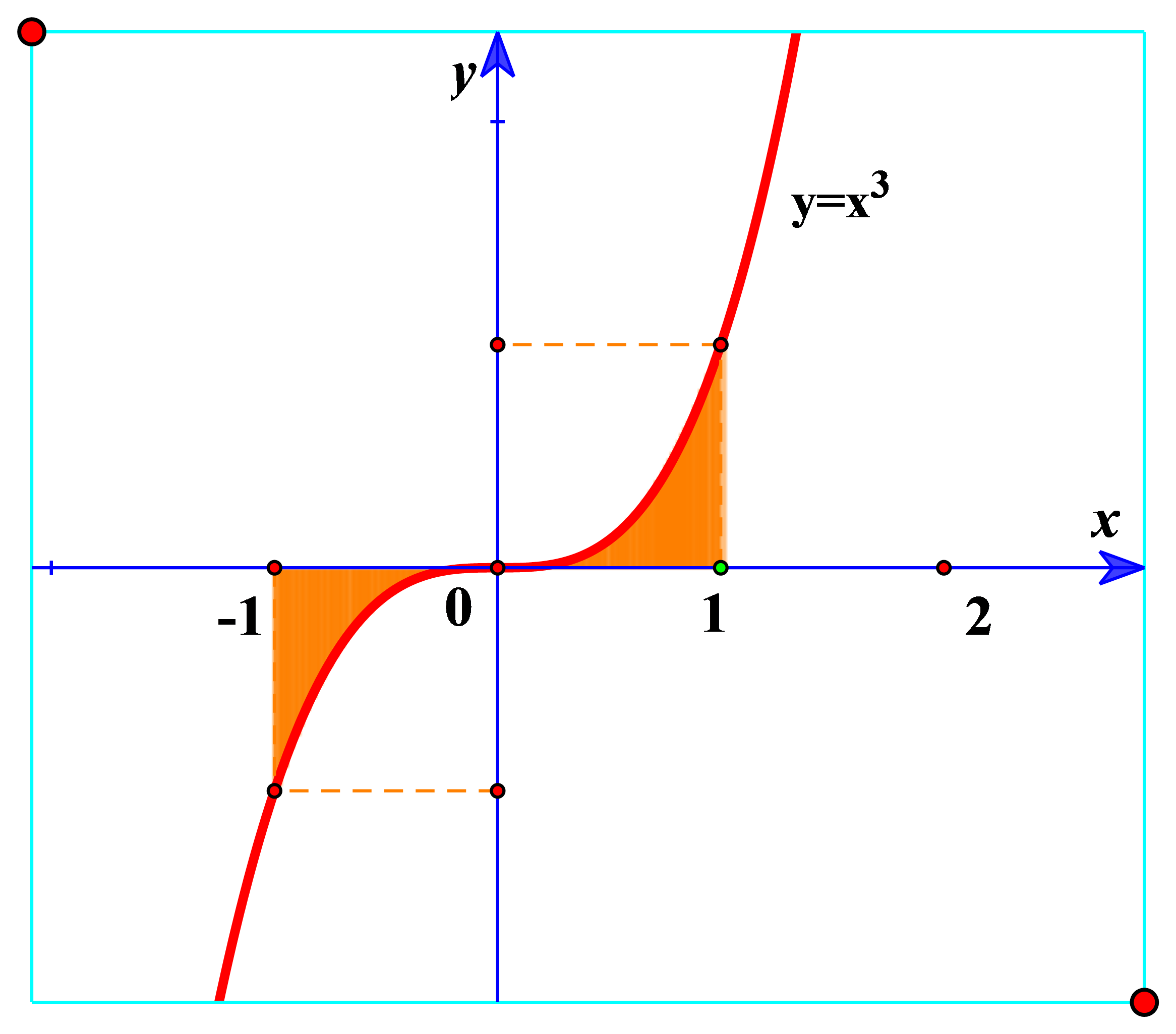
Câu 21:
Câu 22:
Chọn A
Ta cóCâu 24:
ChọnA
Vì M thuộc mặt phẳng ![]()
Ta có: ![]()
Theo giả thiết:
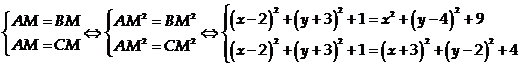
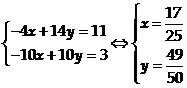
Câu 25:
Chọn A.
DoCâu 26:
Chọn A
Ta cóCâu 27:
Chọn C.
Ta cóCâu 28:
Chọn B
Gọi M(x;y;z);
Do M là điểm nằm trên đoạn BC sao cho MC = 2MB nên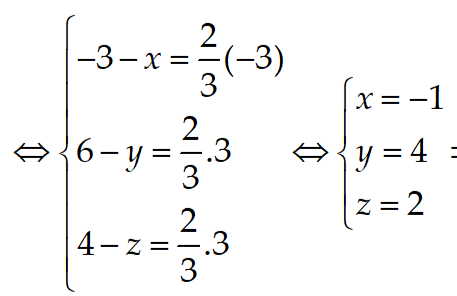
Câu 29:
Chọn D.
Ta có:
Để tam giác ABC vuông tại B khi và chỉ khi:
Do đó:Câu 30:
Trong không gian với hệ tọa độ Oxyz , cho ba vectơ . Khi đó để ba vectơ 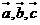 đồng phẳng thì giá trị của tham số thực m bằng bao nhiêu?
đồng phẳng thì giá trị của tham số thực m bằng bao nhiêu?
Chọn C.
Ta có:
Khi đó ba vectơ ![]() đồng phẳng
đồng phẳng ![]()
Câu 31:
Chọn B.
Do ![]() cùng phương
cùng phương
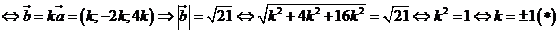
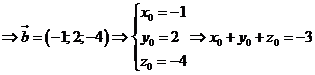
Câu 32:
Chọn A.
Ta cóCâu 33:
Chọn C.
Thử A : ta có ![]()
Thử B : ta có ![]()
Câu 34:
Chọn A
Gọi ta có: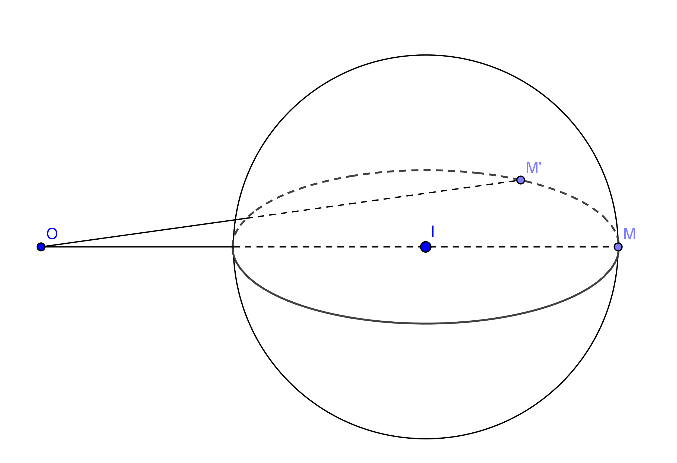
Câu 35:
Chọn B
Gọi là chân đường phân giác kẻ từ đỉnh B.
Ta có:
Theo tính chất đường phân giác ta có: .
Trong đó: