Đề kiểm tra Học kì 2 Toán 12 có đáp án (Mới nhất) - Đề 2
-
3021 lượt thi
-
50 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 1:
Góc tạo bởi đường thẳng và mặt phẳng (P): 3x - 2y = 0 là
Đáp án đúng là: D
Ta có:
và
Vậy suy ra góc giữa đường thẳng (d) và mặt phẳng (P) là góc a, được tính theo công thức
Þ a = arcsin (0) = 0°.
Câu 4:
Cho hàm số f (x) biết . Tích phân bằng
Đáp án đúng là: C
Đặt u = 3x Þ du = 3 dx
Đổi cận:
+) x = 0 Þ u = 0
+) x = 3 Þ u = 9
Khi đó:
Câu 5:
Cho số phức z = 1 + 2i. Môđun số phức bằng
Đáp án đúng là: B
Ta có số phức z = 1 + 2i nên suy ra
Xét các biểu thức:
+)
+)
Ta có xét số phức
Vậy Mô đun của số phức w là
Câu 8:
Trong không gian Oxyz, phương trình mặt phẳng qua điểm M(3; -1; 1) có véc tơ pháp tuyến là
Đáp án đúng là: D
Phương trình mặt phẳng qua điểm M(3; -1; 1) có véc tơ pháp tuyến là
-1.(x - 3) + 3(y + 1) - 2(z - 1) = 0
Û -x + 3 + 3y + 3 - 2z + 2 = 0
Û -x + 3y - 2z + 8 = 0.
Câu 10:
Số phức z = 3a + 4bi với a; b là các số thực khác 0. Số phức z-1 có phần ảo là
Đáp án đúng là: B
z = 3a + 4bi nên suy ra
Vậy phần ảo của số phức z-1 là
Câu 11:
Cho z1 = 2 + 3i; z2 = -1 + 5i. Số phức z1 - z2 là
Đáp án đúng là: C
Số phức z1 - z2 là
z1 - z2 = (2 + 3i) - (-1 + 5i)
= 2 + 3i + 1 - 5i = 3 - 2i.
Câu 12:
Đáp án đúng là: C
có véc-tơ chỉ phương là
Mặt phẳng vuông góc với đường thẳng (d) nên nhận véc-tơ chỉ phương của (d) là làm véc-tơ pháp tuyến
Phương trình mặt phẳng (P) đi qua điểm M(1; -1; 0) và có làm véc-tơ pháp tuyến là
(P): (x - 1) + 2(y + 1) - 2z = 0
Û x + 2y - 2z + 1 = 0.
Câu 13:
Cho số phức z thỏa mãn . Phần thực của z là
Đáp án đúng là: B
Ta có:
Vậy phần thực của số phức z là
Câu 14:
Biết F(x) là một nguyên hàm xủa hàm số f (x) = ex + 2x thỏa mãn F (1) = e. Khi đó, F (x) bằng
Đáp án đúng là: C
Ta có: f (x) = ex + 2x nên suy ra nguyên hàm của f (x) có dạng
= ex + x2 + C
Mà F (1) = e nên suy ra e + 1 + C = e Û C = - 1
Vậy F (x) = ex + x2 - 1.
Câu 15:
Trong không gian Oxyz, phương trình đường thẳng đi qua hai điểm P(1; -1; 2); Q(2; 0; 1) là
Đáp án đúng là: A
Ta có véc-tơ
Phương trình đường thẳng PQ đi qua Q(2; 0; 1) và có véc-tơ chỉ phương là
Câu 16:
Trong hệ tọa độ Oxyz cho M(2; 5; -1) và N(4; 3; 0) độ dài đoạn thẳng MN bằng
Đáp án đúng là: C
Độ dài đoạn thẳng MN bằng
Câu 17:
Đáp án đúng là: D
Nguyên hàm của hàm số trên (0; +¥) là
Mà nên suy ra
Vậy suy ra được
Câu 18:
Cho hai số phức z = 3 + 2i; w = 1 - i. Mô đun của số phức bằng:
Đáp án đúng là: C
Số phức z = 3 + 2i nên suy ra số phức liên hợp của số phức z là
Khi đó mô đun của số phức bằng:
Câu 19:
Số phức liên hợp của số phức z = 5 - 7i là
Đáp án đúng là: D
Số phức liên hợp của số phức z = 5 - 7i là
Câu 20:
Đáp án đúng là: A
Số phức -6 + 3i có phần thực bằng -6.
Câu 21:
Tọa độ tâm mặt cầu (S) đi qua các điểm O(0; 0; 0); A(3; 0; 0); B(3; 0; 3); C(3; 3; 3) là
Đáp án đúng là: D
Gọi I(x; y; z) ta có:
Vậy tâm I của mặt cầu (S) có tọa độ là
Câu 22:
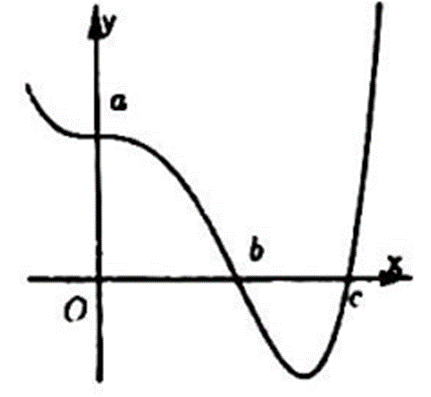
Đáp án đúng là: C
Diện tích hình phẳng giới hạn bởi đồ thị hàm số f (x), x = 0; x = c, trục hoành được tính bởi công thức
Câu 23:
Đáp án đúng là: A
Ta có:
Vậy suy ra khẳng định SAI trong các khẳng định trên là
Câu 24:
Họ tất cả các nguyên hàm F (x) của hàm số với x Î (-¥; 0) là
Đáp án đúng là: B
Họ tất cả các nguyên hàm F (x) của hàm số với x Î (-¥; 0) là
Câu 25:
Cho số phức z = 2 - 2i. Mô đun của số phức bằng
Đáp án đúng là: B
Mô đun của số phức bằng
Câu 26:
Nguyên hàm của hàm số y = 3x là:
Đáp án đúng là: A
Nguyên hàm của hàm số y = 3x là:
Câu 27:
Trong không gian Oxyz, mặt cầu (S): x2 + (y - 4)2 + (z + 1)2 = 25 có tâm là điểm
Đáp án đúng là: C
Trong không gian Oxyz, mặt cầu (S): x2 + (y - 4)2 + (z + 1)2 = 25 có tâm là điểm I(0; 4; -1).
Câu 28:
Diện tích hình phẳng giới hạn bởi các đường bằng
Đáp án đúng là: C
Diện tích hình phẳng giới hạn bởi các đường bằng
Câu 29:
Hàm số f (x) liên tục trên ℝ và có đồ thị như hình bên. Khẳng định nào sau đây là SAI.
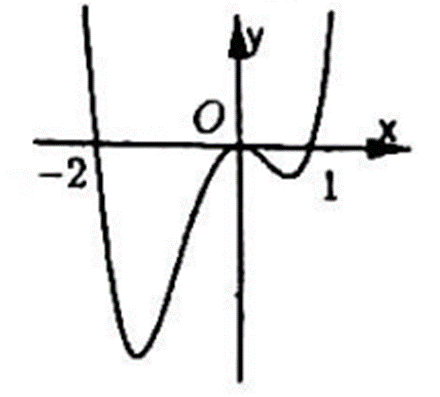
Đáp án đúng là: A
Dựa vào đồ thị hàm số ta thấy diện tích của f(x) và trục hoành trên các khoảng (-2; 0) và (0; 1) là S1 và S2 với:
+)
+)
+) S1 > S2 nên suy ra:
Vậy suy ra mệnh đề SAI trong các mệnh đề sau là
Câu 30:
Nguyên hàm của hàm số f (x) = 3x2 là
Đáp án đúng là: C
Nguyên hàm của hàm số f (x) = 3x2 là
Câu 32:
Diện tích S hình phẳng giới hạn bởi các đường thẳng y = x3 + 1; y = 0; x = 0; x = 1 là
Đáp án đúng là: C
Diện tích S hình phẳng giới hạn bởi các đường thẳng y = x3 + 1; y = 0; x = 0; x = 1 là
Câu 33:
Trong mặt phẳng tọa độ, biết điểm M(3; -4) là điểm biểu diễn số phức z. Mô đun của z bằng
Đáp án đúng là: D
Điểm M(3; -4) là điểm biểu diễn số phức z nên suy ra z = 3 - 4i
Khi đó mô đun của số phức z là
Câu 34:
Đáp án đúng là: A
= (2.3 - 3.2; 2.(-4) - 3.1; 2.1 - 3.5)
= (0; -11; -13).
Câu 35:
Phương trình mặt phẳng đi qua điểm A(1; 2; -1) và vuông góc với hai mặt phẳng có phương trình 2x + y = 0 và x = z + 1
Đáp án đúng là: A
Hai mặt phẳng có phương trình 2x + y = 0 và x = z + 1 lần lượt có hai véc-tơ pháp tuyến là
Phương trình mặt phẳng vuông góc với hai mặt phẳng trên nên suy ra véc-tơ pháp tuyến vuông góc với hai véc-tơ pháp tuyến
Ta suy ra được
= (-1; 2; -1) = -(1; -2; 1)
Phương trình mặt phẳng đi qua A(1; 2; -1) nhận (1; -2; 1) làm véc-tơ pháp tuyến là
(x - 1) - 2(y - 2) + (z + 1) = 0
Û x - 2y + z + 4 = 0.
Câu 36:
Trong hệ tọa độ Oxyz điểm M' đối xứng của điểm N(2; 3; -4) qua gốc tọa độ O có tọa độ
Đáp án đúng là: B và C
Trong hệ tọa độ Oxyz điểm M' đối xứng của điểm N(2; 3; -4) qua gốc tọa độ O có tọa độ M '(-2; -3; 4).
Câu 37:
Hàm số f (x) có đạo hàm liên tục trên đoạn [a; b] và f (a) = -5; f (b) = 1. Tích phân bằng
Đáp án đúng là: A
= f (b) - f (a) = 1 - (-5) = 6.
Câu 38:
Gọi z1; z2 là hai nghiệm của phương trình 2z2 - 5z + 10 = 0. Giá trị của z12 + z22 bằng
Đáp án đúng là: D
z1; z2 là hai nghiệm của phương trình 2z2 - 5z + 10 = 0
Theo Viét:
Khi đó,
z12 + z22 = (z1 + z2)2 - 2z1.z2
Câu 39:
Biết F (x) là một nguyên hàm của hàm số f (x); "x Î (-¥; +¥). Hàm số nào sau đây là một nguyên hàm của hàm số f (x + 2)?
Đáp án đúng là: A
Nguyên hàm F (x) của hàm số f (x)
Đặt u = x + 2 Þ du = dx
Vậy hàm số F (x + 2) là một nguyên hàm của hàm số f (x + 2) với C = 0.
Câu 40:
Tọa độ hình chiếu vuông góc của điểm M(1; -1; 2) trên mặt phẳng (P): 2x - y + 2z + 12 = 0 là
Đáp án đúng là: B
Véc-tơ pháp tuyến của mặt phẳng (P) là:
Phương trình đường thẳng d đi qua M, vuông góc với mặt phẳng (P) nên nhận làm véc-tơ chỉ phương là
Hình chiếu H của điểm M là giao của đường thẳng d mà mặt phẳng (P) nên H(1 + 2t; -1 - t; 2 + 2t) thuộc mặt phẳng (P)
Þ 2(1 + 2t) - (-1 - t) + 2(2 + 2t) + 12 = 0
Û 9t + 19 = 0
Vậy hình chiếu của M lên mặt phẳng (P) có tọa độ
Câu 41:
Trong không gian Oxyz, giao tuyến của hai mặt phẳng x + 2y + z - 1 = 0, 2x - y - z + 4 = 0 là đường thẳng có phương trình là
Đáp án đúng là: B
Giao tuyến của hai mặt phẳng x + 2y + z - 1 = 0, 2x - y - z + 4 = 0 là nghiệm của hệ phương trình
Đặt x = t nên suy ra hệ phương trình (1) trở thành
Vậy suy ra dường thẳng cần tìm có phương trình tham số là
Vậy phương trình đường thẳng d là
Câu 42:
Cho (d): x = y = z; (P): x + z - 1 = 0; (Q): y + 1 = 0. Gọi (D) là đường thẳng giao tuyến của (P) và (Q). Khoảng cách giữa hai đường thẳng (d) và (D) là
Đáp án đúng là: D
Giao tuyến của hai mặt phẳng (P) và (Q) là nghiệm của hệ phương trình
Đặt x = t thì hệ phương trình (1) trở thành
Vậy suy ra phương trình đường thẳng D là:
Chọn M(0; -1; 1) thuộc đường thẳng (D)
(d): x = y = z
Chọn O(0; 0; 0) thuộc đường thẳng (d)
Ta có:
Áp dụng công thức tính khoảng cách của hai đường thẳng
Câu 43:
Phương trình z3 = 1 có ba nghiệm phức phân biệt và A; B; C là các điểm biểu diễn ba số phức đó trên mặt phẳng phức. Trọng tâm tam giác ABC có tọa độ là
Đáp án đúng là: A
z3 = 1 Û (z - 1)(z2 + z + 1) = 0
Vậy suy ra
Trong tâm G của tam giác ABC có tọa độ là
Þ G(0; 0).
Câu 44:
Cho số phức z. Biểu thức |z + 1|2 + |z - 1|2 - 2 có giá trị bằng giá trị của biểu thức nào sau đây
Đáp án đúng là: C
Gọi z = a + bi nên suy ra
|z + 1|2 + |z - 1|2 - 2
= (a + 1)2 + b2 + (a - 1)2 + b2 - 2
= a2 + 2a + 1 + b2 + a2 - 2a + 1 + b2 - 2
= 2(a2 + b2) = 2|z|2.
Câu 45:
Cho hàm số Gọi F (x) là nguyên hàm của hàm số f (x) trên ℝ thỏa mãn F (0) = 2; F (-2) = 1. Giá trị của F (1) - F (-3) bằng
Đáp án đúng là: B
F (x) là nguyên hàm của hàm số f (x) trên ℝ nên ta có:
+) x ³ -1 nên suy ra
Mà F (0) = 2 Þ C1 = 2
Vậy suy ra F (x) = x2 + 3x + 2 (x ³ -1)
Þ F (1) = 1 + 3 + 2 = 6
+) x £ -1 nên suy ra
Mà F (-2) = 1 Þ C2 = 5
Vậy suy ra F (x) = x3 - 2x + 5 (x £ -1)
Þ F (-3) = -27 + 6 + 5 = -16
Khi đó F (1) - F (-3) = 6 + 16 = 22.
Câu 46:
Hàm số y = f (x) có đạo hàm liên tục trên ℝ thỏa mãn f (1) = 1; f (2) = 4. Tích phân bằng
Đáp án đúng là: C
Đặt g (x) = f (x) + 1 Þ g '(x) = f '(x)
và
Vậy khi đó
Câu 47:
Trong không gian Oxyz, phương trình mặt phẳng chứa đường thẳng (d): x - 1 = y - 2 = z + 1 và có khoảng cách đến điểm A(2; 3; -3) lớn nhất có phương trình
Đáp án đúng là: B
Đường thẳng (d): x - 1 = y - 2 = z + 1 có véc-tơ chỉ phương là:
Phương trình tham số của đường thẳng (d) là
Viết phương trình (P) đi qua A và vuông góc với đường thẳng (d) nên nhận làm véc-tơ pháp tuyến
(P): (x - 2) + (y - 3) + (z + 3) = 0
Û x + y + z - 2 = 0
Gọi H là hình chiếu của M lên đường thẳng (d) nên suy ra H là giao điểm của (d) và mặt phẳng (P)
Suy ra H(1 + t; 2 + t; -1 + t) thuộc mặt phẳng (P)
Þ 1 + t + 2 + t + -1 + t - 2 = 0
Û 3t = 0 Û t = 0
Vậy H(1; 2; -1)
Để khoảng cách từ A đến mặt phẳng (Q) chứa (d) là lớn nhất thì AH vuông góc với mặt phẳng (Q)
Mặt phẳng (Q) đi qua H(1; 2; -1) và có làm véc-tơ pháp tuyến là
(Q): -(x - 1) - (y - 2) + 2(z + 1) = 0
Û - x - y + 2z + 5 = 0
Û x + y - 2z - 5 = 0.
Câu 48:
Cho (H) là hình phẳng giới hạn bởi các đường và y = x2. Thể tích khối tròn xoay tạo thành khi quay hình (H) quay quanh trục Ox bằng
Đáp án đúng là: A
Hoành độ giao điểm của hai đồ thị hàm số và y = x2 là nghiệm của phương trình
Thể tích khối tròn xoay tạo thành khi quay hình (H) quay quanh trục Ox bằng
Câu 49:
Biết z1; z2 = 4 + 2i là hai nghiệm của phương trình ax2 + bx + c = 0; (a; b; c Î ℝ và a ¹ 0), Giá trị của T = |z1| + 3|z2| là
Đáp án đúng là: A
Biết z1; z2 = 4 + 2i là hai nghiệm của phương trình ax2 + bx + c = 0 nên z1 = 4 - 2i
Khi đó, T = |z1| + 3|z2|
= |4 - 2i| + 3|4 + 2i|
Câu 50:
Họ nguyên hàm của hàm số trên khoảng (2; +¥) là
Đáp án đúng là: B
Họ nguyên hàm của hàm số trên khoảng (2; +¥) là
