34 câu hỏi trắc nghiệm thuộc Đề kiểm tra Học kì 2 Toán 12 có đáp án (Mới nhất) - Đề 12

Câu 1:

Cho số phức z = a + bi. Khẳng định nào sau đây là khẳng định sai?

A.

|z| = \sqrt{a^{2} + b^{2}};

B. $\bar{\bar{z}} = z;$

C. $\bar{z} = a - b i;$

D. $|z| = \sqrt{a^{2} + {(b i)}^{2}} .$

Xem đáp án

Đáp án đúng là: D

+) $|z| = \sqrt{a^{2} + b^{2}}$ (đúng)

+) $\bar{z} = a - b i \Rightarrow \bar{\bar{z}} = \bar{a - b i} = a + b i = z$ (Đúng)

+) $\sqrt{a^{2} + {(b i)}^{2}} = \sqrt{a^{2} - b^{2}} \neq |z|$ (Sai).

Câu 2:

Cho hàm số y = f (x) liên tục trên [a; b]. Thể tích khối tròn xoay được sinh ra khi cho hình phẳng giới hạn bởi đồ thị y = f (x), Ox, x = a, x = b quay xung quanh Ox là

A. $V = π \int_{a}^{b} f (x) d x;$

B. $V = π \int_{a}^{b} {[f (x)]}^{2} d x;$

C. $V = \int_{a}^{b} {[f (x)]}^{2} d x;$

D. $V = \int_{a}^{b} f (x) d x .$

Xem đáp án

Đáp án đúng là: B

Thể tích khối tròn xoay được sinh ra khi cho hình phẳng giới hạn bởi đồ thị y = f (x), Ox, x = a, x = b quay xung quanh Ox là

$V = π \int_{a}^{b} {[f (x)]}^{2} d x .$

Câu 3:

Trong không gian Oxyz, cho A(1; 2; -1), B(3; 1; 0). Tính độ dài đoạn thẳng AB.

A. $A B = \sqrt{10};$

B. $A B = \sqrt{6};$

C. AB = 5;

D. AB = 3.

Xem đáp án

Đáp án đúng là: B

Độ dài đoạn thẳng AB là:

$A B = \sqrt{{(3 - 1)}^{2} + {(1 - 2)}^{2} + {(0 + 1)}^{2}} = \sqrt{6} .$

Câu 4:

Tích phân $I = \int_{1}^{2} \frac{1}{2 x - 1} d x$ bằng

A. ${[\frac{- 1}{{(2 x - 1)}^{2}}]|}_{1}^{2};$

B. ${[\ln |2 x - 1|]|}_{1}^{2};$

C. ${[\frac{- 1}{2 {(2 x - 1)}^{2}}]|}_{1}^{2};$

D. ${[\frac{1}{2} \ln |2 x - 1|]|}_{1}^{2} .$

Xem đáp án

Đáp án đúng là: D

$I = \int_{1}^{2} \frac{1}{2 x - 1} d x = \frac{1}{2} \int_{1}^{2} \frac{2}{2 x - 1} d x = {[\frac{1}{2} \ln |2 x - 1|]|}_{1}^{2} .$

Câu 5:

Tính thể tích khối tròn xoay tạo nên khi ta cho hình phẳng giới hạn bởi các đường $(C) : y = \sqrt{3 x^{2} + 1}, O x, x = 0, x = 2$ quay quanh trục Ox

A. V = 6p;

B. V = 10p;

C. V = 12p;

D. V = 8p.

Xem đáp án

Đáp án đúng là: B

Thể tích khối tròn xoay tạo nên khi cho hình phẳng giới hạn bởi

(C) : y = \sqrt{3 x^{2} + 1}

,

Ox, x = 0, x = 2 quay quanh trục Ox là:

$V = π \int_{0}^{2} {\sqrt{3 x^{2} + 1}}^{2} d x = π \int_{0}^{2} (3 x^{2} + 1) d x$

$= {π . (x^{3} + x)|}_{0}^{2} = π . (2^{3} + 2) = 10 π .$

Câu 6:

Trong không gian Oxyz, viết phương trình mặt phẳng (P) đi qua điểm M (3; 2; 1) và vuông góc đường thẳng

(d) : \frac{x - 5}{2} = \frac{y + 4}{1} = \frac{z}{- 2} .

A. 2x + y - 2z - 6 = 0;

B. 2x + y - 2z + 5 = 0;

C. 3x + 2y + z - 6 = 0;

D. 3x + 2y + z + 5 = 0.

Xem đáp án

Đáp án đúng là: A

Đường thẳng $(d) : \frac{x - 5}{2} = \frac{y + 4}{1} = \frac{z}{- 2}$ có véc-tơ chỉ phương là $\vec{u} = (2; 1; - 2)$ .

Mặt phẳng (P) đi qua điểm M (3; 2; 1) và vuông góc đường thẳng nên nhận véc-tơ chỉ phương của (d): $\vec{u} = (2; 1; - 2)$ làm véc-tơ pháp tuyến có phương tình là:

(P): 2.(x - 3) + (y - 2) - 2(z - 1) = 0

Û 2x - 6 + y - 2 - 2z + 2 = 0

Û 2x + y - 2z - 6 = 0.

Câu 7:

Trong không gian Oxyz, viết phương trình mặt phẳng (P) đi qua A(1; 0; 0), B(0; -1; 0), C(0; 0; 2)

A. 2x - 2y + z - 2 = 0;

B. 2x + 2y - z - 1 = 0;

C. 2x - 2y + z - 1 = 0;

D. 2x + 2y - z - 2 = 0.

Xem đáp án

Đáp án đúng là: A

Ta có $\vec{A B} = (- 1; - 1; 0)$ và $\vec{A C} = (- 1; 0; 2)$ .

Phương trình mặt phẳng (P) đi qua A(1; 0; 0), B(0; -1; 0), C(0; 0; 2) nên véc-tơ pháp tuyến của (P) vuông góc với $\vec{A B} = (- 1; - 1; 0)$ và $\vec{A C} = (- 1; 0; 2)$

$\Rightarrow \vec{n} = [\vec{A B}; \vec{A C}]$

$= (|\begin{matrix} - 1 & 0 \\ 0 & 2 \end{matrix}|; |\begin{matrix} 0 & - 1 \\ 2 & - 1 \end{matrix}|; |\begin{matrix} - 1 & - 1 \\ - 1 & 0 \end{matrix}|)$

= (-2; 2; -1)

Mặt phẳng (P) đi qua A(1; 0; 0) và có véc-tơ pháp tuyến là (-2; 2; -1) có phương trình

-2(x - 1) + 2y - z = 0

Û 2(x - 1) - 2y + z = 0

Û 2x - 2y + z - 2 = 0.

Câu 8:

Nguyên hàm của hàm số f (x) = 5^x là

A. F (x) = 5^x + C;

B. F (x) = 5^x.ln 5 + C;

C. $F (x) = - \frac{5^{x}}{l n 5} + C;$

D. $F (x) = \frac{5^{x}}{l n 5} + C .$

Xem đáp án

Đáp án đúng là: D

Nguyên hàm của hàm số f (x) = 5^x là

$F (x) = \int f (x) d x = \int 5^{x} d x = \frac{5^{x}}{l n 5} + C .$

Câu 9:

Cho f (x) liên tục trên [a; b] và F (x) là một nguyên hàm của f (x) trên [a; b] thì $\int_{a}^{b} f (x) d x$ bằng

A. F (a) + F (b);

B. F (a).F (b);

C. F (b) - F (a);

D. F (a) - F (b).

Xem đáp án

Đáp án đúng là: C

$\int_{a}^{b} f (x) d x = {F (x)|}_{a}^{b} = F (b) - F (a) .$

Câu 10:

Trong không gian Oxyz, véctơ pháp tuyến của mặt phẳng (P): 2x + y - 3z - 4 = 0 là

A. $\vec{n} = (1; - 3; - 4);$

B. $\vec{n} = (2; - 3; - 4);$

C. $\vec{n} = (2; 1; - 4);$

D. $\vec{n} = (2; 1; - 3) .$

Xem đáp án

Đáp án đúng là: D

Véctơ pháp tuyến của mặt phẳng (P): 2x + y - 3z - 4 = 0 là $\vec{n} = (2; 1; - 3) .$

Câu 11:

Diện tích hình phẳng giới hạn bởi (C):

y = \sqrt{x} - 3, O x, O y

là

A. $S = \int_{0}^{9} (\sqrt{x} - 3) d x;$

B. $S = \int_{0}^{3} (\sqrt{x} - 3) d x;$

C. $S = \int_{0}^{9} |\sqrt{x} - 3| d x;$

D. $S = \int_{0}^{9} |\sqrt{x} - 3| d x .$

Xem đáp án

Đáp án đúng là: C

Hoành độ giao điểm của đồ thị hàm số (C): $y = \sqrt{x} - 3$ và Ox là nghiệm của phương trình: $\sqrt{x} - 3 = 0 \Rightarrow x = 9$

Diện tích hình phẳng giới hạn bởi (C): $y = \sqrt{x} - 3, O x, O y$ là: $S = \int_{0}^{9} |\sqrt{x} - 3| d x .$

Câu 12:

Tìm một nguyên hàm F(x) của f (x) = 3x² - 2x biết F (2) = 9.

A. F (x) = 6x - 3;

B. F (x) = x³ - x² + 5;

C. F (x) = 6x + 9;

D. F (x) = x³ - x² + 9.

Xem đáp án

Đáp án đúng là: B

f (x) = 3x² - 2x

$\Rightarrow F (x) = \int f (x) d x = \int (3 x^{2} - 2 x) d x$

= x³ - x² + C

Mà F (2) = 9 Þ 2³ - 2² + C = 9 Û C = 5

Từ đó suy ra F (x) = x³ - x² + 5.

Câu 13:

Tính

I = \int \frac{x}{\sqrt{x^{2} + 1}} d x

A. I = x² + 1 + C;

B. $I = 2 \sqrt{x^{2} + 1} + C;$

C. $I = \sqrt{x^{2} + 1} + C;$

D. I = ln (x² + 1) + C.

Xem đáp án

Đáp án đúng là: C

$I = \int \frac{x}{\sqrt{x^{2} + 1}} d x = \int \frac{2 x}{2 \sqrt{x^{2} + 1}} d x = \sqrt{x^{2} + 1} + C .$

Câu 14:

Môđun của số phức z = i(3 - 4i) bằng

A. $|z| = \sqrt{10};$

B. |z| = 4;

C. |z| = 5;

D. |z| = 10;

Xem đáp án

Đáp án đúng là: C

Môđun của số phức z = i(3 - 4i) bằng

|z| = |i(3 - 4i)| = |i|.|3 - 4i|

$= 1. \sqrt{3^{2} + 4^{2}} = 5.$

Câu 15:

Trong không gian Oxyz, phương trình tham số của đường thẳng (d) đi qua hai điểm A(0; -1; 3) và B(2; 1; 0) là

A. $\{\begin{matrix} x = 2 - t \\ y = 1 + 2 t \\ z = - 3 t \end{matrix};$

B. $\{\begin{matrix} x = 2 - t \\ y = 1 + 2 t \\ z = 3 t \end{matrix};$

C. $\{\begin{matrix} x = 2 t \\ y = - 1 + t \\ z = 3 - 3 t \end{matrix};$

D. $\{\begin{matrix} x = 2 t \\ y = - 1 + 2 t \\ z = 3 - 3 t \end{matrix} .$

Xem đáp án

Đáp án đúng là: D

Ta có: $\vec{A B} = (2; 2; - 3)$ .

Phương trình tham số của đường thẳng (d) đi qua hai điểm A(0; -1; 3) và nhận $\vec{A B} = (2; 2; - 3)$ làm véc-tơ chỉ phương là:

$(d) : \{\begin{matrix} x = 2 t \\ y = - 1 + 2 t \\ z = 3 - 3 t \end{matrix} .$

Câu 16:

Gọi z₀ là nghiệm phức có phần ảo dương của phương trình z² + 2z + 10 = 0. Điểm nào sau đây là điểm biểu diễn số phức z₀?

A. M(1; -3);

B. N(-1; 3);

C. Q(-1; -3);

D. P(1; 3).

Xem đáp án

Đáp án đúng là: B

Ta có phương trình z² + 2z + 10 = 0

Û z² + 2z + 1 = -9

Û (z + 1)² = 9i²

$\Rightarrow [\begin{matrix} z = - 1 + 3 i \\ z = - 1 - 3 i \end{matrix}$

Ta có z₀ là nghiệm phức có phần ảo dương của phương trình z² + 2z + 10 = 0 nên:

z₀ = -1 + 3i.

Khi đó, điểm biểu diễn của số phức z₀ là N(-1; 3).

Câu 17:

Trong mặt phẳng tọa độ Oxy, điểm M (1; 2) biểu diễn cho số phức nào?

A. z = 2 + i;

B. z = 2 - i;

C. z = 1 + 2i;

D. z = 1 - 2i.

Xem đáp án

Đáp án đúng là: C

M (1; 2) là điểm biểu diễn cho số phức z = 1 + 2i.

Câu 18:

Trong không gian Oxyz, véctơ chỉ phương của đường thẳng $d : \frac{x - 2}{- 1} = \frac{y + 3}{2} = \frac{z - 1}{3}$ là:

A. $\vec{a} = (- 2; 3; - 1);$

B. $\vec{a} = (2; - 3; 1);$

C. $\vec{a} = (1; 2; - 3);$

D. $\vec{a} = (- 1; 2; 3) .$

Xem đáp án

Đáp án đúng là: D

Véctơ chỉ phương của đường thẳng $d : \frac{x - 2}{- 1} = \frac{y + 3}{2} = \frac{z - 1}{3}$ là $\vec{a} = (- 1; 2; 3) .$

Câu 19:

Tính $I = \int_{0}^{1} (e^{x} - 2 x) d x .$

A. I = e + 1;

B. I = 2 - e;

C. I = e;

D. I = e - 2.

Xem đáp án

Đáp án đúng là: D

$I = \int_{0}^{1} (e^{x} - 2 x) d x = {(e^{x} - x^{2})|}_{0}^{1}$

= e - 1 - 1 = e - 2.

Câu 20:

Tìm số phức liên hợp của số phức $z = \frac{4 - 2 i}{1 + i} .$

A. $\bar{z} = 2 - i;$

B. $\bar{z} = 2 + i;$

C. $\bar{z} = 1 + 3 i;$

D. $\bar{z} = 1 - 3 i .$

Xem đáp án

Đáp án đúng là: D

Ta có: $z = \frac{4 - 2 i}{1 + i} = \frac{(4 - 2 i) (1 - i)}{(1 + i) (1 - i)}$

$= \frac{4 - 2 i - 4 i + 2 i^{2}}{1 + 1} = \frac{4 - 6 i - 2}{2}$

$= \frac{2 - 6 i}{2} = 1 - 3 i$

Khi đó số phức liên hợp của số phức $z = \frac{4 - 2 i}{1 + i} = 1 - 3 i$ là:

$\bar{z} = 1 + 3 i .$

Câu 21:

Trong không gian Oxyz, bán kính R của mặt cầu (S): (x - 1)² + y² +(z + 3)² = 4

A. R = 2;

B. R = 6;

C. R = 16;

D. R = 4.

Xem đáp án

Đáp án đúng là: A

Bán kính R của mặt cầu (S): (x - 1)² + y² +(z + 3)² = 4 là R = 2.

Câu 22:

$I = \int 4 x \ln x d x$ bằng

A. x²(2ln x + 1) + C;

B. x²(2ln x - 1) + C;

C. 2x².ln x + C;

D. $\frac{4}{x} + C .$

Xem đáp án

Đáp án đúng là: B

Đặt $\{\begin{matrix} u = \ln x \Leftrightarrow d u = \frac{1}{x} d x \\ d v = 4 x d x \Rightarrow v = 2 x^{2} \end{matrix}$

$\Rightarrow I = \int 4 x \ln x d x = 2 x^{2} . \ln x - \int 2 x d x$

= 2x².ln x - x² + C

= x²(2ln x - 1) + C.

Câu 23:

Diện tích hình phẳng giới hạn bởi các đường y = cos x, y = sin x, x = 0, $x = \frac{π}{3}$ có dạng $S = a + b \sqrt{2} + c \sqrt{3} (a, b, c \in ℝ)$ .Tính giá trị biểu thức P = a + b + c.

A. P = 2;

B. P = 0;

C. P = 1;

D. P = -1.

Xem đáp án

Đáp án đúng là: B

Diện tích hình phẳng giới hạn bởi các đường y = cos x, y = sin x, x = 0, là $x = \frac{π}{3}$

$S = \int_{0}^{\frac{π}{3}} |\cos x - \sin x| d x$

$= \int_{0}^{\frac{π}{4}} |\cos x - \sin x| d x + \int_{\frac{π}{4}}^{\frac{π}{3}} |\cos x - \sin x| d x$

$= \int_{0}^{\frac{π}{4}} (\cos x - \sin x) d x - \int_{\frac{π}{4}}^{\frac{π}{3}} (\cos x - \sin x) d x$

$= {(\sin x + \cos x)|}_{0}^{\frac{π}{4}} - {(\sin x + \cos x)|}_{\frac{π}{4}}^{\frac{π}{3}}$

$= (\frac{\sqrt{2}}{2} + \frac{\sqrt{2}}{2} - 1) - (\frac{\sqrt{3}}{2} + \frac{1}{2} - \frac{\sqrt{2}}{2} - \frac{\sqrt{2}}{2})$

$= \frac{- 3}{2} + 2 \sqrt{2} - \frac{\sqrt{3}}{2}$

Mà lại có $S = a + b \sqrt{2} + c \sqrt{3} (a, b, c \in ℝ)$ nên suy ra

$a = \frac{- 3}{2}, b = 2, c = \frac{- 1}{2}$

Khi đó giá trị biểu thức P = a + b + c

$= \frac{- 3}{2} + 2 + \frac{- 1}{2} = 0.$

Câu 24:

Cho số phức z thỏa mãn điều kiện $2 z - i \bar{z} = 1 - 5 i$ . Phần ảo của số phức z bằng

A. -1;

B. 1;

C. -3;

D. 3.

Xem đáp án

Đáp án đúng là: C

Gọi z = a + bi

Ta có: $2 z - i \bar{z} = 1 - 5 i$

Û 2(a + bi) - i(a - bi) = 1 - 5i

Û (2a - b) + (2b - a) = 1 - 5i

$\Rightarrow \{\begin{matrix} 2 a - b = 1 \\ 2 b - a = - 5 \end{matrix} \Leftrightarrow \{\begin{matrix} a = - 1 \\ b = - 3 \end{matrix}$

Từ đó suy ra z = -1 - 3i

Vậy phần ảo của số phức z bằng -3.

Câu 25:

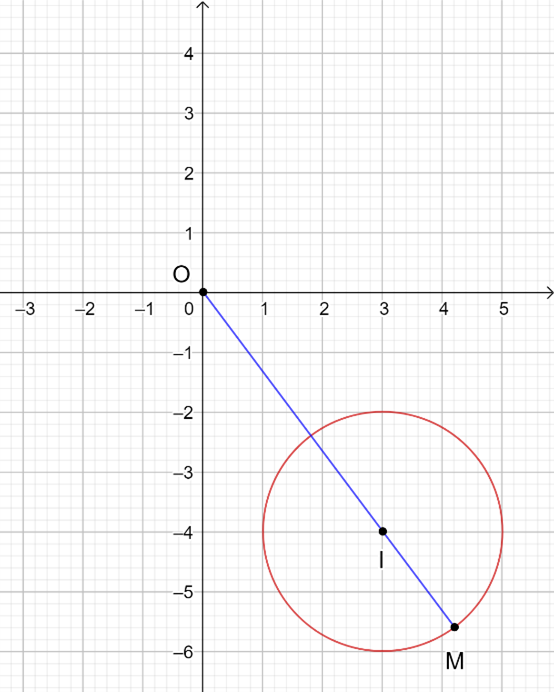
Trong các số phức z thỏa mãn điều kiện |z - 3 + 4i| = 2. Tính mô đun lớn nhất của số phức z.

A. |z| = 7;

B. $|z| = 3 \sqrt{7};$

C. $|z| = \sqrt{7};$

D. |z| = 3.

Xem đáp án

Đáp án đúng là: A

Gọi z = x + yi

Ta có: |z - 3 + 4i| = 2

Û (x - 3)² + (y + 4)² = 4

Vậy M(x; y) là điểm của số phức z trên hệ trục tọa độ và M thuộc đường tròn tâm I(3; -4) bàn kính R = 2

Mô đun của số phức z là $|z| = \sqrt{a^{2} + b^{2}} = O M$ .

Vậy mô đun của số phức z lớn nhất khi OM lớn nhất.

OM lớn nhất khi và chỉ khi M nằm trên đường thẳng OI và xa O nhất

Þ OM = OI + IM

$= \sqrt{3^{2} + {(- 4)}^{2}} + 2 = 5 + 2 = 7$

Vậy mô đun của số phức z lớn nhất bằng 7.

Câu 26:

Trong không gian Oxyz, tìm tọa độ điểm H là hình chiếu vuông góc của điểm M(2; 3; -1) trên mặt phẳng (P): x - y + 2z - 3 = 0.

A. H(3; 2; 1);

B. H(1; -2; 0);

C. H(-3; 2; 4);

D. H (-1; -2; 1).

Xem đáp án

Đáp án đúng là: A

(P): x - y + 2z - 3 = 0 (1)

Suy ra véc-tơ pháp tuyến của mặt phẳng (P) là $\vec{n} = (1; - 1; 2)$ .

Phương trình đường thẳng d vuông góc với mặt phẳng (P) nhận $\vec{n} = (1; - 1; 2)$ làm véc-tơ chỉ phương và đi qua điểm M(2; 3; -1) là

$d : \{\begin{matrix} x = 2 + t \\ y = 3 - t \\ z = - 1 + 2 t \end{matrix}$ (2)

H là hình chiếu vuông góc của điểm M(2; 3; -1) trên mặt phẳng (P) nên H là giao điểm của đường thẳng d và mặt phẳng (P) nên ta có:

Thay (2) vào (1) suy ra:

(2 + t) - (3 - t) + 2(-1 + 2t) - 3 = 0

Û 6t - 6 = 0 Û t = 1

Thay t = 1 vào (2) nên suy ra H(3; 2; 1).

Câu 27:

Cho $\int_{- 2}^{1} f (x) d x = 6$ . Tính $I = \int_{1}^{e} \frac{1}{x} f (1 - 3 \ln x) d x .$

A. I = 2;

B. I = -2;

C. I = 3;

D. I = -3.

Xem đáp án

Đáp án đúng là: A

$I = \int_{1}^{e} \frac{1}{x} f (1 - 3 \ln x) d x$

Đặt u = 1 - 3ln x $\Rightarrow d u = - \frac{3}{x} d x$

Đổi cận:

+) x = 1 Þ u = 1

+) x = e Þ u = -2

Nên suy ra $I = \int_{1}^{e} \frac{1}{x} f (1 - 3 \ln x) d x$

$= \int_{1}^{- 2} - \frac{1}{3} f (u) d u = \frac{1}{3} \int_{- 2}^{1} f (u) d u = \frac{1}{3} .6 = 2.$

Câu 28:

Trong không gian Oxyz, cho mặt phẳng (P): 2x + y - 3z - 5 = 0. Phương trình chính tắc của đường thẳng (d) đi qua A(3; -2; 4) và vuông góc mp (P) là

A. $\frac{x - 3}{2} = \frac{y + 2}{1} = \frac{z - 4}{- 3};$

B. $\frac{x - 2}{3} = \frac{y - 1}{- 2} = \frac{z + 3}{4};$

C. $\frac{x + 3}{2} = \frac{y - 2}{1} = \frac{z + 4}{- 3};$

D. $\frac{x + 2}{3} = \frac{y + 1}{- 2} = \frac{z - 3}{4} .$

Xem đáp án

Đáp án đúng là: A

Mặt phẳng (P): 2x + y - 3z - 5 = 0.

Suy ra véc-tơ pháp tuyến của mặt phẳng (P) là $\vec{n} = (2; 1; - 3)$ .

Phương trình chính tắc của đường thẳng (d) đi qua A(3; -2; 4) và vuông góc mp (P) nhận $\vec{n} = (2; 1; - 3)$ làm véc-tơ chỉ phương là:

$d : \frac{x - 3}{2} = \frac{y + 2}{1} = \frac{z - 4}{- 3} .$

Câu 29:

Diện tích hình phẳng giới hạn bởi (C): y = 3x² - 6x và trục Ox là

A. S = 4;

B. $S = \frac{28}{3};$

C. $S = \frac{14}{3};$

D. S = 8.

Xem đáp án

Đáp án đúng là: A

Hoành độ giao điểm của đồ thị hàm số y = 3x² - 6x và trục Ox là nghiệm của phương trình:

3x² - 6x = 0

Û 3x(x - 2) = 0

$\Rightarrow [\begin{matrix} x = 0 \\ x = 2 \end{matrix}$

Khi đó diện tích hình phẳng giới hạn bởi (C): y = 3x² - 6x và trục Ox là

$S = \int_{0}^{2} |3 x^{2} - 6 x| d x = \int_{0}^{2} (- 3 x^{2} + 6 x) d x$

$= {(- x^{3} + 3 x^{2})|}_{0}^{2} = - 2^{3} + {3.2}^{2} = 4.$

Câu 30:

Trong không gian Oxyz viết phương trình mặt cầu (S) tâm I (2; 0; -1) và tiếp xúc mặt phẳng (P): x - 2y + 2z - 9 = 0.

A. (x - 2)² + y² + (z + 1)² = 9;

B. (x - 2)² + y² + (z + 1)² = 16;

C. (x - 2)² + y² + (z + 1)² = 3;

D. (x - 2)² + y² + (z + 1)² = 4.

Xem đáp án

Đáp án đúng là: A

Mặt cầu (S) tâm I (2; 0; -1) và tiếp xúc mặt phẳng (P): x - 2y + 2z - 9 = 0 nên bán kinh của mặt cầu chính bằng khoảng cahs từ I đến mặt phẳng (P)

$\Rightarrow d_{I / (P)} = R = \frac{|2 + 2. (- 1) - 9|}{\sqrt{1^{2} + {(- 2)}^{2} + 2^{2}}} = \frac{9}{3} = 3$

Mặt cầu (S) tâm I (2; 0; -1) và có bán kính R = 3 có phương trình là

(S): (x - 2)² + y² + (z + 1)² = 9.

Câu 31:

Tính tích phân $I = \int_{0}^{1} (e^{x} - 2 x) d x .$

Xem đáp án

Ta có: $I = \int_{0}^{1} (e^{x} - 2 x) d x = {(e^{x} - x^{2})|}_{0}^{1}$

= e - 1 - 1 = e - 2.

Câu 32:

Tính thể tích khối tròn xoay tạo nên khi cho hình phẳng giới hạn bởi $(C) : y = \sqrt{3 x^{2} + 1}$ , Ox, x = 0, x = 2 quay quanh trục Ox.

Xem đáp án

Thể tích khối tròn xoay tạo nên khi cho hình phẳng giới hạn bởi $(C) : y = \sqrt{3 x^{2} + 1}$ , Ox, x = 0, x = 2 quay quanh trục Ox là:

$V = π \int_{0}^{2} {\sqrt{3 x^{2} + 1}}^{2} d x = π \int_{0}^{2} (3 x^{2} + 1) d x$

$= {π . (x^{3} + x)|}_{0}^{2} = π . (2^{3} + 2) = 10 π .$

Câu 33:

Tìm số phức liên hợp của số phức

z = \frac{4 - 2 i}{1 + i} .

Xem đáp án

Ta có: $z = \frac{4 - 2 i}{1 + i} = \frac{(4 - 2 i) (1 - i)}{(1 + i) (1 - i)}$

$= \frac{4 - 2 i - 4 i + 2 i^{2}}{1 + 1} = \frac{4 - 6 i - 2}{2}$

$= \frac{2 - 6 i}{2} = 1 - 3 i$

Khi đó số phức liên hợp của số phức $z = \frac{4 - 2 i}{1 + i} = 1 - 3 i$ là

$\bar{z} = 1 + 3 i .$

Câu 34:

Trong không gian Oxyz, viết phương trình mặt phẳng (P) đi qua điểm M(3; 2; 1) và vuông góc đường thẳng $(d) : \frac{x - 5}{2} = \frac{y + 4}{1} = \frac{z}{- 2} .$

Xem đáp án

Ta có:

Véc-tơ chỉ phương của đường thẳng (d) là $\vec{u} = (2; 1; - 2)$

Mặt phẳng (P) vuông góc với đường thẳng (d) nên nhận $\vec{u} = (2; 1; - 2)$ làm véc-tơ pháp tuyến

Mặt phẳng (P) đi qua điểm M(3; 2; 1) và nhận $\vec{n} = (2; 1; - 2)$ làm véc-tơ pháp tuyến có phương trình là

(P): 2(x - 3) + 1(y - 2) - 2(z - 1) = 0

Û 2x - 6 + y - 2 - 2z + 2 = 0

Û 2x + y - 2z - 6 = 0.

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đề kiểm tra Học kì 2 Toán 12 có đáp án (Mới nhất)

Đề kiểm tra Học kì 2 Toán 12 có đáp án (Mới nhất) - Đề 12

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương