48 câu hỏi trắc nghiệm thuộc Đề kiểm tra Học kì 2 Toán 12 có đáp án (Mới nhất) - Đề 14

Câu 1:

Cho khối nón có bán kính đáy bằng 2, chiều cao bằng 3. Thể tích của khối nón đã cho bằng

A.18π.

B. 12π.

C. 4π.

D. 6π.

Xem đáp án

Đáp án đúng là A

Thể tích của khối nón đã cho bằng:

V = $\frac{1}{3}$ πR²h = $\frac{1}{3}$ π.2².3 = 4π.

Câu 2:

Trong không gian với hệ tọa độ Oxyz, cho ba điểm A (1; 3; 5), B (2; 0; l), C (0; 9; 0). Tìm tọa độ trọng tâm G của tam giác ABC.

A. G (l; 5; 2).

B. G (1; 4; 2).

C. G (3; 12; 6).

D. G (1; 0; 5).

Xem đáp án

Đáp án đúng là B

x_G= $\frac{x_{A} + x_{B} + x_{C}}{3}$ = $\frac{1 + 2 + 0}{3}$ = 1

y_G= $\frac{y_{A} + y_{B} + y_{C}}{3}$ = $\frac{3 + 0 + 9}{3}$ = 4

z_G= $\frac{z_{A} + z_{B} + z_{C}}{3}$ = $\frac{5 + 1 + 0}{3}$ = 2

Vậy tọa độ điểm G là G (1; 4; 2).

Câu 3:

Cho hai hàm số f (x), g (x) liên tục trên K, a, b ∈ K và k ∈ ℝ . Khẳng định nào sau đây sai?

A. $\int_{a}^{b} f (x) g (x) d x$ = $\int_{a}^{b} f (x) d x$ . $\int_{a}^{b} g (x) d x$ .

B. $\int_{a}^{b} [f (x) - g (x)] d x$ = $\int_{a}^{b} f (x) d x$ − $\int_{a}^{b} g (x) d x$ .

C. $\int_{a}^{b} [f (x) + g (x)] d x$ = $\int_{a}^{b} f (x) d x$ + $\int_{a}^{b} g (x) d x$ .

D. $\int_{a}^{b} k f (x) d x$ = k $\int_{a}^{b} f (x) d x$ .

Xem đáp án

Đáp án đúng là A

Theo tính chất ta có:

$\int_{a}^{b} [f (x) - g (x)] d x$ = $\int_{a}^{b} f (x) d x$ − $\int_{a}^{b} g (x) d x$ suy ra B đúng

$\int_{a}^{b} [f (x) + g (x)] d x$ = $\int_{a}^{b} f (x) d x$ + $\int_{a}^{b} g (x) d x$ suy ra C đúng

$\int_{a}^{b} k f (x) d x$ = k $\int_{a}^{b} f (x) d x$ suy ra D đúng

Vì không có tính chất nào của tích phân là $\int_{a}^{b} f (x) g (x) d x$ = $\int_{a}^{b} f (x) d x$ . $\int_{a}^{b} g (x) d x$ suy ra A sai vậy chọn A.

Câu 4:

Nghiệm của phương trình 3^{x – 1} = 9 là

A. x = 3.

B. x = 2

C. x = −3.

D. x = −2.

Xem đáp án

Đáp án đúng là A

Ta có: 3^{x − 1} = 9

3^{x – 1} = 3²

x –1 = 2

x = 3.

Câu 5:

Cho hàm số f (x) có đạo hàm liên tục trên đoạn [−1; 3] và thỏa mãn f (−1) = 4, f (3) = 7. Giá trị của I = $\int_{- 1}^{3} 5 f' (x) d x$ bằng

A. I = 10.

B. I = 3.

C. I = 15.

D. I = 20.

Xem đáp án

Đáp án đúng là C

Ta có: I = $\int_{- 1}^{3} 5 f' (x) d x$ = ${5 f (x)|}_{- 1}^{3}$

= 5 [ f (3) −f (−1)]

= 5 (7 −4)

= 15.

Câu 6:

Trong không gian với hệ tọa độ Oxyz, phương trình nào sau đây là phương trình chính tắc của đường thẳng đi qua hai điểm A(1;2;−3) và B ( 3 ; −1 ; 1 )

A. $\frac{x - 3}{1}$ = $\frac{y + 1}{2}$ = $\frac{z - 1}{- 3}$ .

B. $\frac{x - 1}{3}$ = $\frac{y - 2}{- 1}$ = $\frac{z + 3}{1}$ .

C. $\frac{x + 1}{2}$ = $\frac{y + 2}{- 3}$ = $\frac{z - 3}{4}$ .

D.

\frac{x - 1}{2}

=

\frac{y - 2}{- 3}

=

\frac{z + 3}{4}

.

Xem đáp án

Đáp án đúng là D

Vì đi qua hai điểm A(1;2;−3)và B ( 3 ; −1 ; 1 ) nên VTCP của đường thẳng đó là: $\vec{u}$ = $\vec{A B}$ = (2; −3; 4)

Phương trình chính tắc của đường thẳng có VTCP là $\vec{u}$ = (2; −3; 4) và đi qua điểm A (1; 2; −3) là:

$\frac{x - 1}{2}$ = $\frac{y - 2}{- 3}$ = $\frac{z + 3}{4}$ .

Câu 7:

Cho hình nón có chiều cao bằng 3 và bán kính đáy bằng 4. Diện tích toàn phần của hình nón là:

A. 36π.

B. 26π.

C. 20π.

D. 16π.

Xem đáp án

Đáp án đúng là A

Hình nón có chiều cao bằng 3 và bán kính đáy bằng 4 nên đường sinh của hình nón có độ dài là: l = $\sqrt{R^{2} + h^{2}}$ = $\sqrt{4^{2} + 3^{2}}$ = 5

Diện tích toàn phần của hình nón là:

S = πRl + πR²= π.4.5 + π.4²= 36π.

Câu 8:

Trong không gian với hệ tọa độ Oxyz, cho điểm M thỏa mãn hệ thức $\vec{O M}$ = 2 $\vec{j}$ + $\vec{k}$ . Tọa độ của điểm M là:

A. M (0; 2; 1).

B. M (1; 2; 0).

C. M (2; 0; 1).

D. M (2; 1; 0).

Xem đáp án

Đáp án đúng là A

Ta có: $\vec{j}$ = (0; 1; 0), $\vec{k}$ = (0; 0; 1)

$\vec{O M}$ = 2 $\vec{j}$ + $\vec{k}$ = (2.0 + 0; 2.1 + 0; 2.0 + 1) = (0; 2; 1)

Vậy tọa độ điểm M là M (0; 2; 1).

Câu 9:

Tập nghiệm S của bất phương trình log₂(x − 1) < 3

A. S = (1; 9).

B. S = (−∞; 9).

C. S = (−∞; 10).

D. S = (1; 10).

Xem đáp án

Đáp án đúng là A

ĐkXĐ: x – 1 > 0 x > 1

Ta có: log₂(x − 1) < 3

x – 1 < 2³

x < 8 + l

x < 9

Kết hợp với điều kiện ta có tập nghiệm của bất phương trình là: S = (1; 9).

Câu 10:

Trong không gian với hệ tọa độ Oxyz, mặt phẳng đi qua tâm của mặt cầu (x − 1)²+ (y + 2)² + z² = 12 và song song với mặt phẳng (Oxz) có phương trình là:

A. y + l = 0.

B. y – 2 = 0.

C. x + z – 1 = 0.

D. y + 2 = 0.

Xem đáp án

Đáp án đúng là D

Gọi tâm của mặt cầu là I

Tọa độ tâm I của mặt cầu là: I (1; –2; 0)

Vì song song với mặt phẳng (Oxz) nên VTPT của mặt phẳng là: $\vec{n}$ = (0; 1; 0)

Phương trình của mặt phẳng có VTPT là $\vec{n}$ = (0; 1; 0) và đi qua điểm I (1; –2; 0) là

0.(x – 1) + 1.(y + 2) + 0.(z – 0) = 0

⇔ y + 2 = 0.

Câu 11:

Cho số phức z = 2 + i. Trên mặt phẳng tọa độ, điểm nào dưới đây biểu diễn số phức w = 2 + iz?

A. Q (2; 1).

B. P (1; 2).

C. N (3; 4).

D. M (3; 2).

Xem đáp án

Đáp án đúng là B

Ta có: w = 2 + iz = 2 + i. (2 + i) = 1 + 2i

Vậy nên điểm biểu diễn của số phức w = 1 + 2i là P (1; 2).

Câu 12:

Cho mặt cầu có diện tích bằng 32πa². Khi đó bán kính của mặt cầu bằng

A. $\frac{a \sqrt{2}}{2}$

B. 2a.

C. $4 \sqrt{2} a$

D. $2 \sqrt{2} a$

Xem đáp án

Đáp án đúng là D

Ta có: S = 4πR²= 32πa²

Do đó R = $\sqrt{\frac{32 π a^{2}}{4 π}}$ = $2 \sqrt{2} a$ .

Câu 13:

Trong các hàm số sau đây, hàm số nào nghịch biến trên ℝ.

A. y = ${(\frac{1}{2})}^{- x}$ .

B. y = ${(\sqrt{3})}^{x}$ .

C. y = ${(\frac{2}{e})}^{x}$ .

D. y =

{(\frac{π}{3})}^{x}

.

Xem đáp án

Đáp án đúng là C

Hàm số mũ: y = a^x (a > 0 và a ≠ 1) nghịch biến trên ℝ khi 0 < a < 1.

Ta có:

+) y = ${(\frac{1}{2})}^{- x} = 2^{x}$ và 2 > 1 nên y = ${(\frac{1}{2})}^{- x}$ là hàm đồng biến trên ℝ.

+) $\sqrt{3} > 1$ nên y = ${(\sqrt{3})}^{x}$ là hàm đồng biến trên ℝ.

+) $0 < \frac{2}{e} < 1$ nên y = ${(\frac{2}{e})}^{x}$ là hàm nghịch biến trên ℝ.

+) $\frac{π}{3} > 1$ nên y = ${(\frac{π}{3})}^{x}$ là hàm đồng biến trên ℝ.

Vậy nên hàm số nghịch biến trên ℝ là y = ${(\frac{2}{e})}^{x}$ .

Câu 14:

Cho C là hằng số, khẳng định nào sau đây đúng?

A. $\int x^{2} d x$ = $\frac{x^{3}}{3}$ + C.

B. $\int x^{2} d x$ = x + C.

C. $\int x^{2} d x$ = 2x + C.

D.

\int x^{2} d x

= x³ + C.

Xem đáp án

Đáp án đúng là A

Áp dụng công thức: $\int x^{n} d x$ = $\frac{x^{n + 1}}{n + 1}$ + C

Suy ra nguyên hàm của $\int x^{2} d x$ = $\frac{x^{3}}{3}$ + C.

Câu 15:

Gọi S là diện tích hình phẳng giới hạn bởi các đường y = x² + 2x + 1; y = m (m < 0) và x = 0; x = 1. Biết S = 4, khẳng định nào sau đây đúng?

A. m ∈ (−3; −2).

B. m ∈ (−6; −3).

C. m ∈ (−2; −1).

D. m ∈ (−1; 0).

Xem đáp án

Đáp án đúng là C

Ta có: Diện tích hình phẳng bằng 4 nên

S = $\int_{0}^{1} |x^{2} + 2 x + 1 - m| d x$ = 4

Vì đồ thị của hàm số y = x² + 2x + 1 nằm trên trục hoành mà m < 0 nên x² + 2x + 1 – m > 0

$\Leftrightarrow$ $\int_{0}^{1} |x^{2} + 2 x + 1 - m| d x$ = 4 = 4

$\Leftrightarrow$ ${(\frac{x^{3}}{3} + x^{2} + x - m x)|}_{0}^{1}$ = 4

$\Leftrightarrow$ $\frac{1^{3}}{3} + 1^{2} + 1 - m .1$ = 4

$\Leftrightarrow$ m = −4 + $\frac{1}{3}$ + 2

$\Leftrightarrow$ m = $\frac{- 5}{3}$ .

Câu 16:

Xét các số thực a, b thỏa mãn điều kiện log₅(5^a.125^b) = log₁₂₅5. Khẳng định nào dưới đây đúng?

A. 3a + 9b = 1.

B. 9ab = 1

C. a + 3b = 2.

D. 9a + 3b = 1.

Xem đáp án

Đáp án đúng là A

Ta có: log₅(5^a.125^b) = log₁₂₅5

log₅(5^a.5^3b) = $\frac{1}{3}$ log₅5

log₅(5^a.5^3b) = $\log_{5} 5^{\frac{1}{3}}$

5^{a + 3b}= $5^{\frac{1}{3}}$

a + 3b = $\frac{1}{3}$

3a + 9b = 1.

Câu 17:

Trong không gian với hệ tọa độ Oxyz , cho ba điểm A (1; 2; −1), B (2; −1; 3), C (−3, 5; l) . Tìm tọa độ điểm D sao cho tứ giác ABCD là hình bình hành.

A. D (−2; 8; −3).

B. D (−2; 2; 5) .

C. D (−4; 8; −3) .

D. D (−4; 8; −5).

Xem đáp án

Đáp án đúng là C

Để ABCD là hình bình hành thì:

x_D = x_A+ x_C– x_B= 1 – 3 – 2 = – 4

y_D = y_A+ y_C– y_B= 2 + 5 + 1 = 8

z_D = z_A+ z_C– z_B= – 1 + 1 – 3 = – 3

Vậy tọa độ điểm D là D (−4; 8; −3).

Câu 18:

Trên mặt phẳng phức, tập hợp các điểm biểu diễn của số phức z = x + yi thỏa mãn |z + 2 + i| = | $\bar{z}$ – 3i| là đường thẳng có phương trình

A. y = −x + 1.

B. y = x −1.

C. y = −x −1.

D. y = x + 1.

Xem đáp án

Đáp án đúng là A

Thay z = x + yi, $\bar{z}$ = x – yi vào biểu thức |z + 2 + i| = | $\bar{z}$ – 3i| ta được:

|x + yi + 2 + i| = |x – yi – 3i|

$\Leftrightarrow$ |(x + 2) + (y + 1)i| = |x – (y + 3)i|

$\Leftrightarrow$ (x + 2)² + (y + 1)²= x² + (y + 3)²

$\Leftrightarrow$ x² + 4x + 4 + y² + 2y + 1 = x² + y² + 6y + 9

$\Leftrightarrow$ 4x + 4 + 2y + 1 = 6y + 9

$\Leftrightarrow$ 6y – 2y = – 4x – 4 – 1 + 9

$\Leftrightarrow$ 4y = – 4x + 4

$\Leftrightarrow$ y = – x + 1.

Câu 19:

Cho x, y > 0 và α, β ∈ ℝ . Khẳng định nào sau đây sai?

A. (xy)^α = x^α. y^α.

B. x^α. y^β = x^α+β.

C. x^α+ y^β = (x + y)^α.

D. (x^α)^β = x^αβ.

Xem đáp án

Đáp án đúng là C

Theo tính chất, ta có:

(xy)^α = x^α. y^α vậy đáp án A đúng

x^α. y^β = x^α+β vậy đáp án B đúng

(x^α)^β = x^αβvậy đáp án B đúng

Không có tính chất nào là x^α+ y^β = (x + y)^α vậy nên đáp án C là đáp án sai. Do đó chọn C.

Câu 20:

Trong không gian với hệ tọa độ Oxyz, cho đường thẳng (d): $\frac{x + 1}{- 2}$ = $\frac{y - 1}{3}$ = $\frac{2 - z}{1}$ . Vectơ nào sau đây là một vectơ chỉ phương của đường thẳng (d)?

A. $\vec{u_{d}}$ = (2; −3; 1).

B. $\vec{u_{d}}$ = (−1; 1; 2).

C. $\vec{u_{d}}$ = (−2; 3; 1).

D.

\vec{u_{d}}

= (−2; −3; −1).

Xem đáp án

Đáp án đúng là A

Ta có phương trình đường thẳng (d) là:

$\frac{x + 1}{- 2}$ = $\frac{y - 1}{3}$ = $\frac{2 - z}{1}$

$\Leftrightarrow$ $\frac{x + 1}{- 2}$ = $\frac{y - 1}{3}$ = $\frac{z - 2}{- 1}$

Suy ra VTCP của d là $\vec{u_{d}}$ = (2; −3; 1).

Câu 21:

Biết $\int_{- 1}^{4} f (x) d x$ = $\frac{1}{2}$ và $\int_{- 1}^{0} f (x) d x$ = − $\frac{1}{2}$ .Tính tích phân I = $\int_{0}^{4} [4 e^{2 x} + 2 f (x)] d x$

A. I = 2e⁸.

B. I = 2e⁸– 4.

C. I = 4e⁸.

D. I = 4e⁸– 2.

Xem đáp án

Đáp án đúng là A

Ta có: $\int_{- 1}^{0} f (x) d x$ = − $\frac{1}{2}$ $\Rightarrow$ $\int_{0}^{- 1} f (x) d x$ = $\frac{1}{2}$

$\int_{0}^{4} f (x) d x$ = $\int_{0}^{- 1} f (x) d x$ + $\int_{- 1}^{4} f (x) d x$ = $\frac{1}{2}$ + $\frac{1}{2}$ = 1

I = $\int_{0}^{4} [4 e^{2 x} + 2 f (x)] d x$ = $\int_{0}^{4} 4 e^{2 x} d x$ + 2 $\int_{0}^{4} f (x) d x$

= ${2 e^{2 x}|}_{0}^{4}$ + 2

= 2e⁸– 2 + 2

= 2e⁸.

Câu 22:

Kí hiệu z₁, z₂ là hai nghiệm phức của phương trình 2z² – 4z + 11 = 0. Giá trị biểu thức P = 2z₁z₂+ 2z₁+ 2z₂bằng

A. 17.

B. 11.

C. 13.

D. 15.

Xem đáp án

Đáp án đúng là D

Ta có: z₁+ z₂= – $\frac{b}{a}$ = – $\frac{- 4}{2}$ = 2

z₁z₂= $\frac{c}{a}$ = $\frac{11}{2}$

Vậy P = 2z₁z₂+ 2z₁+ 2z₂

= 2. $\frac{11}{2}$ + 2.2

= 15.

Câu 23:

Tập xác định của hàm số y = (2 – )^x là

A. (0; + ∞)

B. (–∞; + ∞)

C. (–∞; 0)

D. (0; + ∞)

Xem đáp án

Đáp án đúng là D

Tập xác định của hàm số y = (2 – $\sqrt{3}$ )^x là x ∈ (–∞; + ∞)

Câu 24:

Cho hình phẳng (H) giới hạn bởi các đường y = x², y = 2x. Thể tích của khối tròn xoay được tạo thành khi quay (H) xung quanh trục Ox bằng:

A. $\frac{64 π}{15}$

B. $\frac{32 π}{15}$

C. $\frac{21 π}{15}$

D. $\frac{16 π}{15}$

Xem đáp án

Đáp án đúng là A

Hoành độ giao điểm của hai đồ thị hàm số y = x² và y = 2x là:

x² = 2x

$\Leftrightarrow$ x² – 2x = 0

$\Leftrightarrow$ x. (x – 2) = 0

$\Leftrightarrow$ $[\begin{array}{l} x = 0 \\ x - 2 = 0 \end{array}$

$\Leftrightarrow$ $[\begin{array}{l} x = 0 \\ x = 2 \end{array}$

Thể tích của khối tròn xoay được tạo thành khi quay hình phẳng (H) được giới hạn bởi các đường y = x², y = 2x, x = 0 và x = 2 xung quanh trục Ox là:

V = π. $\int_{0}^{2} |{(x^{2})}^{2} - {(2 x)}^{2}| d x$

Với x ∈ [0; 2] thì x⁴ – 4x² = x². (x²– 4) < 0 nên | x⁴ – 4x²| = – x⁴ + 2x²

Vậy nên V = π. $\int_{0}^{2} (- x^{4} + 4 x^{2}) d x$

= π. ${(- \frac{x^{5}}{5} + \frac{4 x^{3}}{3})|}_{0}^{2}$

= π. ${(- \frac{2^{5}}{5} + \frac{{4.2}^{3}}{3})|}_{0}^{2}$

= $\frac{64 π}{15}$

Câu 25:

Trong không gian vói hệ tọa độ Oxyz, cho mặt phẳng (P): 3x −z + 2 = 0. Vectơ nào dưới đây là một vectơ pháp tuyến của (P) ?

A. $\vec{n}$ = (3; −1; 0).

B. $\vec{n}$ = ( −1; 0; −1).

C. $\vec{n}$ = (3; 0; −1).

D.

\vec{n}

= (3; −1; 2).

Xem đáp án

Đáp án đúng là C

Mặt phẳng (P) có vectơ pháp tuyến là $\vec{n}$ = (a; b; c) thì có phương trình mặt phẳng là:

ax + by + cz + d = 0

Vậy nên vectơ pháp tuyến của mặt phẳng (P): 3x −z + 2 = 0 có vectơ pháp tuyến là:

$\vec{n}$ = (3; 0; −1).

Câu 26:

Cho hai số phức z₁ = 2 − i và z₂ = l + i. Số phức 2z₁ + z₂ là

A. −3i.

B. 3.

C. 5 − i.

D. −1 + 5i

Xem đáp án

Đáp án đúng là C

Ta có: 2z₁ + z₂= 2(2 – i) + l + i

= 4 – 2i + l + i

= 5 − i.

Câu 27:

Đạo hàm của hàm số y = 2^x là

A. 2^x ln2.

B. 2^x.

C. x. $2^{x - 1}$ .

D.

\frac{2^{x}}{\ln 2}

.

Xem đáp án

Đáp án đúng là A

Áp dụng công thức: = a^x. lna

Ta được: (2^x) = 2^x ln2.

Câu 28:

Cho hàm số y = f (x) liên tục trên [a; b] , viết công thức tính diện tích hình phẳng được giới hạn bởi đồ thị hàm số y = f (x), trục Ox và các đường thẳng x = a, x = b (a < b).

A. π $\int_{a}^{b} f (x) d x$ .

B. π $\int_{a}^{b} f^{2} (x) d x$ .

C. $\int_{a}^{b} |f (x)| d x$ .

D.

\int_{a}^{b} f^{2} (x) d x

.

Xem đáp án

Đáp án đúng là C

Công thức tính diện tích hình phẳng được giới hạn bởi đồ thị hàm số y = f (x), trục Ox và các đường thẳng x = a, x = b (a < b) là:

S = $\int_{a}^{b} |f (x)| d x$ .

Câu 29:

Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): x + 2y + 3z − 6 = 0 điểm nào sau đây thuộc mặt phẳng (P) ?

A. Q (1; 2; 1).

B. P (3; 2; 0).

C. M (1; 2; 3).

D. N (1; 1; 1)

Xem đáp án

Đáp án đúng là D

+) Thay tọa độ điểm Q(1; 2; 1) vào phương trình mặt phẳng (P) ta được:

⇔1+ 2.2 + 3.1 − 6 = 0

⇔ 2 = 0 (vô lí)

Vậy nên điểm Q(1; 2; 1) không thuộc mặt phẳng (P).

+) Thay tọa độ điểm P (3; 2; 0) vào phương trình mặt phẳng (P) ta được:

⇔3+ 2.2 + 3.0 − 6 = 0

⇔ 1 = 0 (vô lí)

Vậy nên điểm P (1; 2; 3) không thuộc mặt phẳng (P).

+) Thay tọa độ điểm P (1; 2; 3) vào phương trình mặt phẳng (P) ta được:

⇔1 + 2.2 + 3.3 − 6 = 0

⇔ 8 = 0 (vô lí)

Vậy nên điểm P (1; 2; 3) không thuộc mặt phẳng (P).

+) Thay tọa độ điểm N (1; 1; 1) vào phương trình mặt phẳng (P) ta được:

⇔1+ 2.1 + 3.1 − 6 = 0

⇔ 0 = 0 (luôn đúng)

Vậy nên điểm N (1; 1; 1) thuộc mặt phẳng (P).

Câu 30:

Với a > 0, a ≠ 1, $\log_{a^{3}} a$ bằng:

A. − $\frac{1}{3}$ .

B. 3.

C. −3

D.

\frac{1}{3}

.

Xem đáp án

Đáp án đúng là D

Ta có: = $\frac{1}{3}$ log_a a = $\frac{1}{3}$ .

Câu 31:

Trong không gian với hệ tọa độ Oxyz, cho điểm M (2; 1; 4) và đường thẳng ∆: $\frac{x - 1}{1}$ = $\frac{y - 2}{1}$ = $\frac{z - 1}{2}$ .Tìm tọa độ điểm H là hình chiếu vuông góc của điểm M trên đường thẳng ∆.

A. H (3; 4; 5).

B. H (1; 2; 1)

C. H (2; 3; 3)

D. H (0; 1; −1).

Xem đáp án

Đáp án đúng là C

Ta có: $\vec{n_{Δ}}$ = (1; 1; 2)

∆: $\frac{x - 1}{1}$ = $\frac{y - 2}{1}$ = $\frac{z - 1}{2}$ = t

Điểm H ∈ ∆ nên tọa độ điểm H là H (t +1; t + 2; 2t + 1)

$\vec{M H}$ = (t +1− 2; t +2 − 1; 2t +1− 4) = (t – 1; t + 1; 2t – 3)

Vì H là hình chiếu vuông góc của điểm M lên ∆ nên

$\vec{M H}$ . $\vec{n_{Δ}}$ = 0

$\Leftrightarrow$ 1.(t – 1) + 1.(t + 1) + 2. (2t – 3) = 0

$\Leftrightarrow$ 6t – 6 = 0

$\Leftrightarrow$ t = 1

Vậy tọa độ điểm H là H (2; 3; 3).

Câu 32:

Số phức liên hợp của z = 3 −4i là:

A. 3 −4i.

B. −3 −4i.

C. −3 + 4i.

D. 3 + 4i

Xem đáp án

Đáp án đúng là D

Số phức liên hợp của z = a + bi là $\bar{z}$ = a – bi

Vậy nên số phức liên hợp của z = 3 −4i là $\bar{z}$ = 3 + 4i

Câu 33:

Gọi z₁, z₂ là nghiệm của phương trình z² – 2z + 2 = 0. Biết số phức z₁ có phần ảo âm. Phần ảo của số phức z₂

A. 1.

B. 1 − i.

C. i.

D. −1.

Xem đáp án

Đáp án đúng là A

Ta có: ∆ = b² – 4ac = (–2)² – 4.1.2 = – 4

$\sqrt{Δ}$ = ± 2i

Z₁= $\frac{- b - \sqrt{Δ}}{2 a}$ = $\frac{- (- 2) - 2 i}{2.1}$ = 1 – i

z₂= $\frac{- b + \sqrt{Δ}}{2 a}$ = $\frac{- (- 2) + 2 i}{2.1}$ = 1 + i

Vậy phần ảo của số phức z₂ là bằng 1.

Câu 34:

Cho C là hằng số, khẳng định nào sau đây đúng?

A. $\int \sin (2 x + \frac{π}{3}) d x$ = $\frac{1}{2} c o s (2 x + \frac{π}{3})$ + C.

B. $\int \sin (2 x + \frac{π}{3}) d x$ = – $\frac{1}{2} c o s (2 x + \frac{π}{3})$ + C.

C. $\int \sin (2 x + \frac{π}{3}) d x$ = – $\frac{1}{2}$ cos2x + C.

D.

\int \sin (2 x + \frac{π}{3}) d x

=

\frac{1}{2}

cos2x + C.

Xem đáp án

Đáp án đúng là B

Áp dụng công thức: $\int \sin (a x + b) d x$ = – $\frac{1}{a}$ cos (ax+ b) + C

Vậy nên $\int \sin (2 x + \frac{π}{3}) d x$ = – $\frac{1}{2} c o s (2 x + \frac{π}{3})$ + C.

Câu 35:

Cho $\int_{- 2}^{1} f (x) d x$ = 3. Tính tích phân $\int_{- 2}^{1} [2 f (x) - 1] d x$

A. −3.

B. 3.

C. −9.

D. 5.

Xem đáp án

Đáp án đúng là B

$\int_{- 2}^{1} [2 f (x) - 1] d x$ = 2. $\int_{- 2}^{1} f (x) d x$ − $\int_{- 2}^{1} 1 d x$

= 2.3 − ${x|}_{- 2}^{1}$

= 6 − 1− 2

= 3.

Câu 36:

Trong không gian với hệ tọa độ Oxyz , viết phương trình mặt phẳng tiếp xúc với mặt cầu (S): (x – 1)² + y² + (z + 2)² = 6 đồng thời song song với hai đường thẳng d₁:

\frac{x - 2}{3}

=

\frac{y - 1}{- 1}

=

\frac{z}{- 1}

, d₂:

\frac{x}{1}

=

\frac{y + 2}{1}

=

\frac{z - 2}{- 1}

A. x − y + 2z + 9 = 0.

B. $[\begin{array}{l} x + y + 2 z - 3 = 0 \\ x + y + 2 z + 9 = 0 \end{array}$

C. x + y + 2z + 9 = 0.

D. $[\begin{array}{l} x - y + 2 z - 3 = 0 \\ x - y + 2 z + 9 = 0 \end{array}$

Xem đáp án

Đáp án đúng là B

Gọi tên phương trình mặt phẳng tiếp xúc với mặt cầu (S): (x – 1)² + y² + (z + 2)² = 6 đồng thời song song với hai đường thẳng d₁: $\frac{x - 2}{3}$ = $\frac{y - 1}{- 1}$ = $\frac{z}{- 1}$ , d₂: $\frac{x}{1}$ = $\frac{y + 2}{1}$ = $\frac{z - 2}{- 1}$ P . Gọi tâm của mặt cầu (S) là I.

Ta có: Tọa độ tâm I của mặt cầu (S) là: I (1; 0; −2), bán kính mặt cầu bằng $\sqrt{6}$

$\vec{u_{d_{1}}}$ = (3; −1; −1)

$\vec{u_{d_{2}}}$ = (1; 1; −1)

Vì mặt phẳng (P) song song với hai đường thẳng d₁và d₂ vậy nên:

$\vec{n_{(P)}}$ = $[\vec{u_{d_{1}}}; \vec{u_{d_{2}}}]$ = [(−1). (−1) − (−1).1; (−1). 1 – 3. (−1);3.1 – (−1).1]

= (2; 2; 4) = (1; 1; 2)

Vậy phương trình mặt phẳng (P) có dạng là: x + y + 2z + d = 0

Vì mặt phẳng (P) tiếp xúc với mặt cầu (S) nên:

d(I, (P)) = $\frac{|1 + 0 + 2. (- 2) + d|}{\sqrt{1^{2} + 1^{2} + 2^{2}}}$ = $\sqrt{6}$

$\Leftrightarrow$ |d – 3| = 6

$\Leftrightarrow$ $[\begin{array}{l} d - 3 = - 6 \\ d - 3 = 6 \end{array}$

$\Leftrightarrow$ $[\begin{array}{l} d = - 3 \\ d = 9 \end{array}$

Vậy phương trình mặt phẳng (P) là: $[\begin{array}{l} x + y + 2 z - 3 = 0 \\ x + y + 2 z + 9 = 0 \end{array}$ .

Câu 37:

Cho số phức z thỏa mãn |z| = 5. Tập hợp các điểm biểu diễn số phức w = 2( $\bar{z}$ − 3) + 1 − 4i là một đường tròn có bán kính bằng

A. 10.

B. 11.

C. 5.

D.

\frac{5}{2}

.

Xem đáp án

Đáp án đúng là A

Đặt w = a + bi

Ta có: w = 2( $\bar{z}$ − 3) + 1 − 4i

w −1+ 4i = 2 $\bar{z}$ − 6

w + 5 + 4i = 2 $\bar{z}$

|w + 5 + 4i| = |2 $\bar{z}$ |

|a + 5 + (b + 4) i| = 2.5

(a + 5)² + (b + 4)² = 100

Vậy tập hợp các điểm biểu diễn số phức w = 2( $\bar{z}$ − 3) + 1 − 4i là một đường tròn có bán kính bằng 10.

Câu 38:

Cho hàm số y = f (x) có đạo hàm liên tục trên khoảng (1; +∞) thỏa mãn [xf '(x) − 2 f (x)] lnx = x³ – f (x), ∀ x ∈ (1; + ∞); và f ( $\sqrt[3]{e}$ ) = 3e. Giá trị nhỏ nhất của hàm số y = f (x) trên khoảng (1; +∞) thuộc khoảng nào dưới đây?

A. (6; 8).

B. (4; 6).

C. (10; 12).

D. (8; 10).

Xem đáp án

Đáp án đúng là B

Hàm số y = f (x) có đạo hàm liên tục trên khoảng (1; +∞) và [xf '(x) − 2f (x)] lnx = x³−f(x)

$\Rightarrow$ 2f '(x) = $\frac{f (x) + x^{3}}{\ln x}$ (1), x ∈ (1; +∞)

Ta có: f ( $\sqrt[3]{e}$ ) = 3e f (x) = 3lnx (2)

Từ (1) và (2) suy ra y = f (x) có giá trị nhỏ nhất là:

$\frac{2 f' (x) - f (x)}{\ln x}$ = $\frac{3 + \ln 3}{1}$ ≈ 4, 09.

Câu 39:

Cho hình lăng trụ tam giác đều ABC.A'B'C' có độ dài cạnh đáy bằng a , độ dài cạnh bên bằng 2a. Thể tích của khối cầu ngoại tiếp hình lăng trụ đó bằng

A. $\frac{32 π}{3 \sqrt{3}}$ a³.

B. $\frac{16 π \sqrt{3}}{27}$ a³.

C. $\frac{32 π}{27}$ a³.

D.

\frac{32 π \sqrt{3}}{27}

a³.

Xem đáp án

Đáp án đúng là D

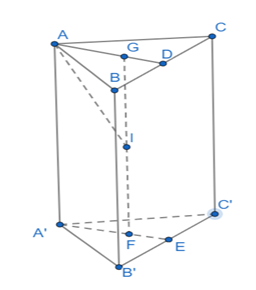
Gọi G là trọng tâm của ∆ ABC nằm trên đường trung tuyến AD của ∆ ABC, F là trọng tâm của ∆ A'B'C'

Vậy GF song song với AA' và bằng AA' bằng 2a

Gọi I là trung điểm của GF vậy nên IG = a

Vì là lăng trụ tam giác đều ABC.A'B'C' nên I là tâm của mặt cầu ngoại tiếp lăng trụ tam giác đều ABC.A'B'C'

AD là đường trung tuyến của tam giác đều ∆ ABC cạnh a nên:

AD = $\frac{a \sqrt{3}}{2}$ $\Rightarrow$ AG = $\frac{2}{3} . \frac{a \sqrt{3}}{2}$ = $\frac{a \sqrt{3}}{3}$

R = IA = $\sqrt{I G^{2} + A G^{2}}$ = $\sqrt{a^{2} + {(\frac{a \sqrt{3}}{3})}^{2}}$ = $\frac{2 a \sqrt{3}}{3}$

Vậy thể tích của khối cầu là:

V = $\frac{4}{3}$ πR³= $\frac{4}{3}$ π. ${(\frac{2 a \sqrt{3}}{3})}^{3}$ = $\frac{32 π \sqrt{3}}{27}$ a³.

Bán kính của khối cầu ngoại tiếp hình lăng trụ là:

Câu 40:

Cho bất phương trình log₇(x² +2x + 2) + 1 > log₇(x² + 6x + 5 + m). Có tất cả bao nhiêu giá trị nguyên của m để bất phương trình trên có tập nghiệm chứa khoảng (1; 3)?

A. 36.

B. 34.

C. vô số.

D. 35 .

Xem đáp án

Đáp án đúng là A

Bất phương trình $\Leftrightarrow$ $\{\begin{cases} x^{2} + 6 x + 5 + m > 0 \\ \log_{7} [7 (x^{2} + 2 x + 2)] > \log_{7} (x^{2} + 6 x + 5 + m) \end{cases}$

$\Leftrightarrow$ $\{\begin{cases} m > - x^{2} - 6 x - 5 \\ 6 x^{2} + 8 x + 9 > m \end{cases}$ ,∀ x ∈ (1; 3) (*)

Với f (x) = −x² – 6x – 5; g(x) = 6x² + 8x + 9. Xét sự biến thiên của hai hàm số f (x) và g (x)

+ f '(x) = −2x – 6 < 0, ∀ x ∈ (1; 3) f (x) luôn nghịch biến trên khoảng (1; 3)

$\Rightarrow$ $\max_{[1; 3]}$ f (x) = f (1) = –12

+g'(x) = 12x + 8 > 0, ∀ x ∈ (1; 3) g (x) luôn đồng biến trên khoảng (1; 3)

$\Rightarrow$ $\min_{[1; 3]}$ g (x) = g (1) = 23

Lúc này (*) $\Leftrightarrow$ $\{\begin{cases} m \geq \max_{[1; 3]} f (x) \\ m \leq \min_{[1; 3]} g (x) \end{cases}$

Khi đó –12≤ m≤ 23. Mà m∈ ℤ nên m ∈ {–12; –11; –10;…..; 22; 23}

Vậy có tất cả 36 giá trị nguyên của m thỏa mãn yêu cầu bài toán.

Câu 41:

Cho hàm số y = f (x) có đạo hàm liên tục trên R, đồ thị hàm số f '(x) như hình vẽ dưới đây. Giá trị nhỏ nhất của hàm số g (x) = f (x) − $\frac{x^{2}}{2}$ trên đoạn [−2; 1] là

Media VietJack

A. g (−1)

B. g (−2)

C. g (0)

D. g (1)

Xem đáp án

Đáp án đúng là C

Ta có: g (x) = f (x) − $\frac{x^{2}}{2}$ $\Rightarrow$ g' (x) = f '(x) – x

g' (x) = 0 $\Leftrightarrow$ f '(x) – x = 0

f '(x) – x = 0 $\Rightarrow$ x = –2; x= 0; x = 1

Vì g' (x) = f '(x) – x nên g' (x) = 0 $\Leftrightarrow$ f '(x) – x = 0

Do đó nghiệm của g' (x) = 0 cũng là x = –2;x= 0; x = 1

Lập bảng biến thiên của g (x) ta được:

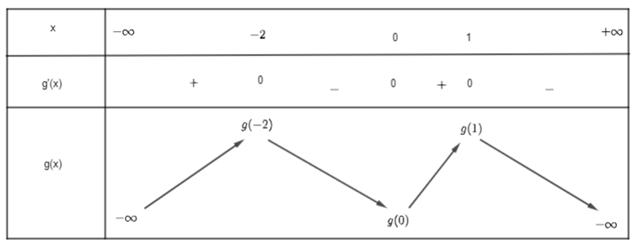
Từ bảng biến thiên ta có thể thấy giá trị nhỏ nhất của hàm số g (x) = f (x) − $\frac{x^{2}}{2}$ trên đoạn [−2; 1] là g (0).

Câu 42:

Cho hàm số f (x) có đạo hàm liên tục trên R. Biết

\int_{0}^{1} (x - 1) f' (x) d x

= 12 và f (0) = 3. Tính

\int_{0}^{1} f (x) d x

.

A. −9.

B. 9.

C. 15.

D. 36.

Xem đáp án

Đáp án đúng là A

Đặt u = x –1 du = dx

dv = f (x)dx v = f (x) + C

Chọn C = 0 v = f (x)

$\int_{0}^{1} (x - 1) f' (x) d x$ = ${f (x) . (x - 1)|}_{0}^{1}$ – $\int_{0}^{1} f (x) d x$ = 12

$\Leftrightarrow$ f (1). 0 – f (0). (0 – 1) – $\int_{0}^{1} f (x) d x$ = 12

$\Leftrightarrow$ – 3. (–1) – $\int_{0}^{1} f (x) d x$ = 12

$\Leftrightarrow$ $\int_{0}^{1} f (x) d x$ = –9.

Câu 43:

Xét các số phức z thỏa mãn |z² – 2z + 5|= |(z – 1 + 2i)(z + 3i – 1)|. Giá trị nhỏ nhất của biểu thức P = |z – 2 + 2i| bằng

A. $\frac{5}{2}$ .

B. $\frac{3}{2}$ .

C. $\sqrt{5}$ .

D.1

Xem đáp án

Đáp án đúng là B

Đặt z = a + bi

Ta có: |z² – 2z + 5|= |(z – 1 + 2i)(z + 3i – 1)|

|(z – 1 – 2i). (z – 1 + 2i)| = |(z – 1 + 2i)(z + 3i – 1)|

|z – 1 – 2i| = |z + 3i – 1|

(a – 1)² + (b – 2)² = (a – 1)² + (b + 3)²

– 4b + 4 = 6b +9

– 10b = 5

b = – $\frac{1}{2}$

P_min = |z – 2 + 2i|_min= ${\sqrt{{(a - 2)}^{2} + {(b + 2)}^{2}}}_{\min}$ = ${\sqrt{{(a - 2)}^{2} + {(- \frac{1}{2} + 2)}^{2}}}_{\min}$ a = 2

Vậy nên P_min = $\sqrt{{(- \frac{1}{2} + 2)}^{2}}$ = $\frac{3}{2}$ .

Câu 44:

Phương trình 2log₂(2x + 3) = log₂x² có số nghiệm là

A. 2.

B. 3.

C. 0 .

D. 1.

Xem đáp án

Đáp án đúng là D

ĐKXĐ: $\{\begin{cases} 2 x + 3 > 0 \\ x^{2} > 0 \end{cases} \Leftrightarrow \{\begin{cases} x > - \frac{3}{2} \\ x \neq 0 \end{cases}$

Ta có: 2log₂(2x + 3) = log₂x²

$\Leftrightarrow$ log₂(2x + 3)² = log₂x²

$\Leftrightarrow$ (2x + 3)² = x²

^{$\Leftrightarrow$ $\{\begin{cases} 2 x + 3 = - x \\ 2 x + 3 = x \end{cases}$}

^{$\Leftrightarrow$ $\{\begin{cases} 3 x = - 3 \\ x = - 3 \end{cases}$}

^{$\Leftrightarrow$ $\{\begin{cases} x = - 1 \\ x = - 3 \end{cases}$}

Trong hai nghiệm trên thì có x = −1 thỏa mãn.

Vậy phương trình đã cho có 1 nghiệm

Câu 45:

Có tất cả bao nhiêu giá trị nguyên của tham số m để phương trình 2^2x+4− $3^{x^{2}}$ .m = 0 có hai nghiệm thực phân biệt?

A. 24.

B. 18. .

C. Vô số.

D. 31

Xem đáp án

Đáp án đúng là A

Ta có: 2^2x+4− $3^{x^{2}}$ .m = 0

$\Leftrightarrow$ 2^2x+4= $3^{x^{2}}$ .m

$\Leftrightarrow$ log₃ = log₃(m. $3^{x^{2}}$ )

$\Leftrightarrow$ (2x + 4).log₃2= log₃m + x²

$\Leftrightarrow$ x²– 2x.log₃2 + log₃m – 4log₃2 = 0

$\Leftrightarrow$ x²– 2x.log₃2 + log₃ = 0

Để phương trình có hai nghiệm phân biệt thì:

∆' > 0

$\Leftrightarrow$ (log₃2)²– log₃ $\frac{m}{16}$ > 0

$\Leftrightarrow$ log₃ $\frac{m}{16}$ < (log₃2)²

$\Leftrightarrow$ $\frac{m}{16}$ < $3^{\log_{3}^{2} 2}$

$\Leftrightarrow$ m < 16. $3^{\log_{3}^{2} 2}$ = 24, 77 mà m > 0

Nên m ∈ {1; 2; 3; 4;….;24}

Vậy có 24 số m thỏa mãn yêu cầu bài toán.

Câu 46:

Cho C là hằng số, khẳng định nào sau đây đúng?

A. $\int \frac{d x}{2 x + 1}$ dx = $\frac{1}{2}$ .ln|4x + 2| + C.

B. $\int \frac{d x}{2 x + 1}$ dx = $\frac{1}{2}$ ln (2x + 1) + C.

C. $\int \frac{d x}{2 x + 1}$ dx =2ln|2x + 1| + C.

D.

\int \frac{d x}{2 x + 1}

dx =ln|2x +1| + C.

Xem đáp án

Đáp án đúng là B

Áp dụng công thức: $\int \frac{d x}{a x + b} d x$ = $\frac{1}{a}$ .ln|ax + b| + C

Vậy nên: $\int \frac{d x}{2 x + 1}$ dx = $\frac{1}{2}$ ln |2x + 1| + C.

Câu 47:

Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d: $\frac{x + 1}{2}$ = $\frac{y - 1}{1}$ = $\frac{z - 2}{3}$ và mặt phẳng (P): x − y − z − 1 = 0. Phương trình chính tắc của đường thẳng đi qua điểm M (1; 1; −2), song song với (P) và vuông góc với d là

A. $\frac{x + 1}{2}$ = $\frac{y}{1}$ = $\frac{z + 5}{3}$ .

B. $\frac{x + 1}{- 2}$ = $\frac{y - 2}{1}$ = $\frac{z + 5}{- 3}$ .

C. $\frac{x - 1}{2}$ = $\frac{y - 1}{5}$ = $\frac{z + 2}{- 3}$ .

D.

\frac{x - 1}{2}

=

\frac{y - 1}{1}

=

\frac{z + 2}{3}

.

Xem đáp án

Đáp án đúng là C

Gọi tên đường thẳng đi qua điểm M (1; 1; −2), song song với (P) và vuông góc với d là d₁

Gọi VTCP của đường thẳng d₁ cần tìm là $\vec{u}$ = (a; b; c)

Ta có: $\vec{n_{(P)}}$ = (1; −1; −1), $\vec{u_{d}}$ = (2; 1; 3)

Vì d₁ // (P) $\vec{u_{d_{1}}}$ . $\vec{n_{(P)}}$ = 0

$\Rightarrow$ a – b – c = 0

Vì d₁ ⊥ d $\vec{u_{d_{1}}}$ . $\vec{u_{d}}$ = 0

$\Rightarrow$ 2a + b + 3c = 0

Từ (1) và (2) suy ra: $\{\begin{cases} a = \frac{2 b}{5} \\ c = \frac{- 3 b}{5} \end{cases}$

Vậy $\vec{u}$ = $(\frac{2 b}{5}; b; \frac{- 3 b}{5})$

Hay $\vec{u_{d_{1}}}$ = (2; 5; –3)

Phương trình chính tắc của đường thẳng có VTCP là

\vec{u_{d_{1}}}

= (2; 5; –3) và đi qua điểm M

(1; 1; −2) là:

$\frac{x - 1}{2}$ = $\frac{y - 1}{5}$ = $\frac{z + 2}{- 3}$ .

Câu 48:

Bất phương trình $2^{x^{2} - 3 x + 4}$ ≤ ${(\frac{1}{2})}^{x - 12}$ có bao nhiêu nghiệm nguyên không dương?

A. 5.

B. 4.

C. 3.

D. 6.

Xem đáp án

Đáp án đúng là C

Ta có: $2^{x^{2} - 3 x + 4}$ ≤ ${(\frac{1}{2})}^{x - 12}$

$\Leftrightarrow$ $2^{x^{2} - 3 x + 4}$ ≤ $2^{- (x - 12)}$

$\Leftrightarrow$ x²−3x +4 ≤ −x +12

$\Leftrightarrow$ x²−3x + x + 4 −12 ≤ 0

$\Leftrightarrow$ x²−2x −8≤ 0

$\Leftrightarrow$ − 2 ≤ x ≤ 4

Vậy bất phương trình có 3 nghiệm nguyên không dương là −2; −1; 0.

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đề kiểm tra Học kì 2 Toán 12 có đáp án (Mới nhất)

Đề kiểm tra Học kì 2 Toán 12 có đáp án (Mới nhất) - Đề 14

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương