50 câu hỏi trắc nghiệm thuộc Đề kiểm tra Học kì 2 Toán 12 có đáp án (Mới nhất) - Đề 10

Câu 1:

Cho các số thực x, y thỏa 3x + y - 3xi = 2y - 1 + (x - y)i. Khi đó giá trị của M = x + y là:

A. M = -5;

B. M = 5;

C. M = 4;

D. M = -4.

Xem đáp án

Đáp án đúng là: B

Ta có:

3x + y - 3xi = 2y - 1 + (x - y)i

Û (3x + y) + (-3x)i = (2y - 1) + (x - y)i

$\Rightarrow \{\begin{matrix} 3 x + y = 2 y - 1 \\ - 3 x = x - y \end{matrix} \Leftrightarrow \{\begin{matrix} 3 x - y = - 1 \\ - 4 x + y = 0 \end{matrix}$

$\Leftrightarrow \{\begin{matrix} - x = - 1 \\ 3 x - y = - 1 \end{matrix} \Leftrightarrow \{\begin{matrix} x = 1 \\ y = 3 x + 1 \end{matrix}$

$\Leftrightarrow \{\begin{matrix} x = 1 \\ y = 4 \end{matrix}$

Vậy suy ra: M = x + y = 1 + 4 = 5.

Câu 2:

Họ nguyên hàm của hàm số y = 2x là:

A. 2x² + C;

B. 2;

C. 2x + C;

D. x² + C.

Xem đáp án

Đáp án đúng là: D

Họ nguyên hàm của hàm số y = 2x là:

$\int 2 x d x = x^{2} + C .$

Câu 3:

Trong không gian Oxyz, cho ba điểm A(-1; 1; 1), B(2; 1; 0) và C(1; -1; 2). Mặt phẳng đi qua điểm A và vuông góc với BC có phương trình là:

A. -x + y + z - 1 = 0;

B. x + 2y - 2z - 1 = 0;

C. x + 2y - 2z + 1 = 0;

D. 3x + 2z + 1.

Xem đáp án

Đáp án đúng là: C

Ta có: $\vec{B C} = (- 1; - 2; 2)$

Mặt phẳng vuông góc với BC nên BC là véc-tơ pháp tuyến của mặt phẳng $\Rightarrow \vec{n} = (- 1; - 2; 2)$

Mặt phẳng đi qua điểm A(-1; 1; 1) có véc-tơ pháp tuyến là $\vec{n} = (- 1; - 2; 2)$

-1.(x + 1) - 2.(y - 1) + 2.(z - 1) = 0

Û - x - 2y + 2z - 1 = 0

Û x + 2y - 2z + 1 = 0.

Câu 4:

Số phức liên hợp của số phức z = (2 + 7i)(-1 + 3i) là:

A. $\bar{z} = - 23 + i;$

B. $\bar{z} = - 23 - i;$

C. $\bar{z} = 23 - i;$

D. $\bar{z} = 23 + i .$

Xem đáp án

Đáp án đúng là: A

z = (2 + 7i)(-1 + 3i)

= -2 + 6i - 7i + 21.i²

= -2 + 6i - 7i - 21

= -23 - i

$\Rightarrow \bar{z} = - 23 + i .$

Câu 5:

Tính tích phân $I = \int_{1}^{3} {(x - 1)}^{2022} d x$ ta được kết quả nào sau đây:

A. $I = \frac{2^{2021}}{2021};$

B. $I = \frac{2^{2022}}{2022};$

C. $I = \frac{2^{2023}}{2023};$

D. $I = \frac{2^{2024}}{2024} .$

Xem đáp án

Đáp án đúng là: C

$I = \int_{1}^{3} {(x - 1)}^{2022} d x$

$= \int_{1}^{3} \frac{2023. {(x - 1)}^{2022}}{2023} d x$

$= {\frac{1}{2023} . {(x - 1)}^{2023}|}_{1}^{3}$

$= \frac{1}{2023} . {(3 - 1)}^{2023} = \frac{2^{2023}}{2023} .$

Câu 6:

Rút gọn biểu thức P = (1 + i)²⁰²² ta được kết quả nào sau đây:

A. P = -2¹⁰¹¹i;

B. P = 2¹⁰¹¹i;

C. P = -2¹⁰¹¹;

D. P = 2¹⁰¹¹.

Xem đáp án

Đáp án đúng là: A

Ta có:

(1 + i)² = 1 + 2i + i² = 1 + 2i - 1 = 2i

Þ (1 + i)⁴ = (2i)² = 4i² = -4

Vậy suy ra

P = (1 + i)²⁰²² = (1 + i)^4.505+2

= (1 + i)^4.505.(1 + i)²

= (-4)⁵⁰⁵.2i = -2¹⁰¹⁰.2i = -2¹⁰¹¹i.

Câu 7:

Trong không gian Oxyz, cho các vectơ $\vec{a} = (1; 2; - 3), \vec{b} = (2; 1; 1), \vec{c} = (- 3; 1; 0) .$ Tìm tọa độ của vectơ $\vec{u} = 3 \vec{a} + 2 \vec{b} - \vec{c}$

A. $\vec{u} = (- 10; - 7; 7);$

B. $\vec{u} = (4; 9; - 7);$

C. $\vec{u} = (10; 7; 7);$

D. $\vec{u} = (10; 7; - 7) .$

Xem đáp án

Đáp án đúng là: D

$\vec{u} = 3 \vec{a} + 2 \vec{b} - \vec{c}$

$= 3. (1; 2; - 3) + 2 (2; 1; 1) - (- 3; 1; 0)$

= (3.1 + 2.2 + 3; 3.2 + 2.1 - 1; 3.(-3) + 2.1)

= (10; 7; -7).

Câu 8:

Biết hàm số f (x) có đạo hàm $f' (x)$ liên tục trên ℝ và $\int_{0}^{2} (x - 2) f' (x) d x = 7, f (0) = 1.$ Tính $I = \int_{0}^{2} f (x) d x .$

A. I = -9;

B. I = -7;

C. I = 7;\

D. I = -5.

Xem đáp án

Đáp án đúng là: D

$\int_{0}^{2} (x - 2) f' (x) d x = 7$

Đặt $\{\begin{matrix} u = x - 2 \\ d v = f' (x) d x \end{matrix} \Rightarrow \{\begin{matrix} d u = d x \\ v = f (x) \end{matrix}$

Vậy suy ra

$\int_{0}^{2} (x - 2) f' (x) d x$

$= {(x - 2) . f (x)|}_{0}^{2} - \int_{0}^{2} f (x) d x$

$= - (0 - 2) . f (0) - \int_{0}^{2} f (x) d x$

= 2 - I = 7

Þ I = -5.

Câu 9:

Cho số phức z₁ = 1 + 3i và z₂ = -3 + 2i. Môđun của số phức w = z₁ + 2z₂ là:

A. $|w| = \sqrt{29};$

B. $|w| = \sqrt{65};$

C. $|w| = 2 \sqrt{29};$

D. $|w| = \sqrt{74} .$

Xem đáp án

Đáp án đúng là: D

w = z₁ + 2z₂ = (1 + 3i) + 2(-3 + 2i)

= 1 + 3i - 6 + 4i = - 5 + 7i

$\Rightarrow |w| = \sqrt{{(- 5)}^{2} + 7^{2}} = \sqrt{74} .$

Câu 10:

Cho f (x) liên tục trên ℝ và $\int_{2}^{5} f (x) d x = 10.$ Khi đó $\int_{2}^{5} [4 f (x) + 2] d x$ bằng:

A. 32;

B. 46;

C. 36;

D. 43.

Xem đáp án

Đáp án đúng là: B

$\int_{2}^{5} [4 f (x) + 2] d x = 4 \int_{2}^{5} f (x) d x + {2 x|}_{2}^{5}$

= 4.10 + 2.5 - 2.2 = 46.

Câu 11:

Trong không gian Oxyz, cho hai điểm A(2; 1; 0), B(-2; 3; 2) và đường thẳng $d : \frac{x - 1}{2} = \frac{y}{1} = \frac{z}{- 2} .$ Phương trình mặt cầu đi qua hai điểm A, B và có tâm nằm trên đường thẳng d là:

A. (x + 1)² + (y + 1)² + (z - 2)² = 17;

B. (x - 1)² + (y + 1)² + (z - 2)² = 9;

C. (x - 1)² + (y - 1)² + (z - 2)² = 5;

D. (x + 1)² + (y + 1)² + (z + 2)² = 16.

Xem đáp án

Đáp án đúng là: A

$d : \frac{x - 1}{2} = \frac{y}{1} = \frac{z}{- 2}$

$\Rightarrow \{\begin{matrix} x = 1 + 2 t \\ y = t \\ z = - 2 t \end{matrix}$

Mặt cầu tâm O thuộc đường thẳng d nên tọa độ điểm O là O(1 + 2t; t; -2t)

Phương trình mặt cầu đi qua hai điểm A, B nên OA = OB

Hay OA² = OB²

Þ (1 + 2t - 2)² + (t - 1)² + (-2t)² = (1 + 2t + 2)² + (t - 3)² + (-2t - 2)²

Û (2t - 1)² + (t - 1)² + (-2t)² = (2t + 3)² + (t - 3)² + (-2t - 2)²

Û 4t² - 4t + 1 + t² - 2t + 1 + 4t² = 4t² + 12t + 9 + t² - 6t + 9 + 4t² + 8t + 4

Û 20t + 20 = 0

Û t = -1

Vậy O(-1; -1; 2)

Ta có bán kính

$= \sqrt{{(2 + 1)}^{2} + {(1 + 1)}^{2} + {(0 - 2)}^{2}} = \sqrt{17}$

Phương trình mặt cầu tâm O(-1; -1; 2) và có bán kính $R = \sqrt{17}$ là:

(x + 1)² + (y + 1)² + (z - 2)² = 17.

Câu 12:

Gọi S là diện tích của hình phẳng giới hạn bởi các đồ thị hàm số y = x² + 3 và y = 4x. Mệnh đề nào sau đây đúng?

A. $S = \int_{1}^{3} |x^{2} - 4 x + 3| d x;$

B. $S = \int_{1}^{3} (x^{2} - 4 x + 3) d x;$

C. $S = \int_{1}^{3} (x^{2} + 4 x + 3) d x;$

D. $S = \int_{1}^{3} |x^{2} + 4 x + 3| d x .$

Xem đáp án

Đáp án đúng là: A

Hoành độ giao điểm của hai đồ thị hàm số y = x² + 3 và y = 4x là nghiệm của phương trình

x² + 3 = 4x

Û x² - 4x + 3 = 0

Û x² - 3x - x + 3 = 0

Û x(x - 3) - (x - 3) = 0

Û (x - 1). (x - 3) = 0

$\Rightarrow \{\begin{matrix} x - 1 = 0 \\ x - 3 = 0 \end{matrix} \Leftrightarrow \{\begin{matrix} x = 1 \\ x = 3 \end{matrix}$

S là diện tích của hình phẳng giới hạn bởi các đồ thị hàm số y = x² + 3 và y = 4x nên

$S = \int_{1}^{3} |(x^{2} + 3) - 4 x| d x = \int_{1}^{3} |x^{2} - 4 x + 3| d x .$

Câu 13:

Biết

\int_{3}^{4} \frac{d x}{x^{2} + x} = a \ln 4 + b \ln 3 + c \ln 5

với a, b Î ℤ. Tính S = a + 2b + 3c

A. S = -1;

B. S = -3;

C. S = 1;

D. S = 0.

Xem đáp án

Đáp án đúng là: B

$\int_{3}^{4} \frac{d x}{x^{2} + x} = \int_{3}^{4} \frac{d x}{x (x + 1)} = \int_{3}^{4} \frac{(x + 1) - x}{x (x + 1)} d x$

$= \int_{3}^{4} (\frac{1}{x} - \frac{1}{x + 1}) d x = {[\ln x - \ln (x + 1)]|}_{3}^{4}$

= ln 4 - ln 5 - ln 3 + ln 4

= 2.ln 4 - ln 3 - ln 5

Mà $\int_{3}^{4} \frac{d x}{x^{2} + x} = a \ln 4 + b \ln 3 + c \ln 5$

Þ a = 2, b = c = -1

Vậy S = a + 2b + 3c = 2 + 2.(-1) +3.(-1) = -3.

Câu 14:

Cho số phức z thỏa mãn điều kiện (3 + 2i)z + (2 - i)² = 20 + 3i. Hiệu phần thực và phần ảo của số phức z là:

A. -4;

B. 4;

C. 6;

D. -6.

Xem đáp án

Đáp án đúng là: C

Đặt: z = a + bi

(3 + 2i)z + (2 - i)² = 20 + 3i

Þ (3 + 2i).(a + bi) + (2 - i)² = 20 + 3i

Û 3a + 3bi + 2ai + 2bi² + 4 - 4i + i² = 20 + 3i

Û 3a + 3bi + 2ai - 2b + 4 - 4i - 1 = 20 + 3i

Û (3a - 2b - 17) + (3b + 2a - 7).i = 0

$\Rightarrow \{\begin{matrix} 3 a - 2 b - 17 = 0 \\ 3 b + 2 a - 7 = 0 \end{matrix} \Leftrightarrow \{\begin{matrix} 3 a - 2 b = 17 \\ 2 a + 3 b = 7 \end{matrix}$

$\Rightarrow \{\begin{matrix} a = 5 \\ b = - 1 \end{matrix}$

Vậy hiệu phần thực và phần ảo của số phức z là: a - b = 5 - (-1) = 6.

Câu 15:

Trong không gian Oxyz, cho hai điểm A (1; 2; 3), B(1; 2; 1) và M là một điểm nằm trên mặt phẳng Oxy. Tìm tọa độ điểm M để $P = |\vec{M A} + \vec{M B}|$ đạt giá trị nhỏ nhất.

A. M(1; 2; 0);

B. M(1; 2; 2);

C. M(0; 2; 1);

D. M(-1; 1; 0).

Xem đáp án

Đáp án đúng là: A

M là một điểm nằm trên mặt phẳng Oxy Þ M(x; y; 0)

$P = |\vec{M A} + \vec{M B}|$

$= |(1 - x; 2 - y; 3) + (1 - x; 2 - y; 1)|$

$= |(2 - 2 x; 4 - 2 y; 4)|$

$= \sqrt{{(2 - 2 x)}^{2} + {(4 - 2 y)}^{2} + 4^{2}}$

$= 2 \sqrt{{(x - 1)}^{2} + {(y - 2)}^{2} + 4}$

Vậy P_min khi (x - 1)² + (y - 2)² + 4 đạt GTNN

Þ x = 1, y = 2

Vậy M(1; 2; 0).

Câu 16:

Họ Nguyên hàm của hàm số y = cos 2x là:

A. $- \frac{1}{2} \sin 2 x + C;$

B. - sin 2x + C;

C. sin 2x + C;

D. $\frac{1}{2} \sin 2 x + C .$

Xem đáp án

Đáp án đúng là: D

Họ Nguyên hàm của hàm số y = cos 2x là:

$\int \cos 2 x d x = \frac{1}{2} \int 2 \cos 2 x d x$

$= \frac{1}{2} \sin 2 x + C .$

Câu 17:

Biết $\int_{3}^{4} \frac{x + 1}{x - 2} d x = a + b \ln 2$ với a, b Î ℤ. Tính S = 2a + b

A. S = 5;

B. S = 7;

C. S = 1;

D. S = -1.

Xem đáp án

Đáp án đúng là: A

$\int_{3}^{4} \frac{x + 1}{x - 2} d x = \int_{3}^{4} \frac{x - 2 + 3}{x - 2} d x = \int_{3}^{4} (1 + \frac{3}{x - 2}) d x$

$= {x + 3 \ln (x - 2)|}_{3}^{4} = 4 + 3 \ln 2 - 3 = 1 + 3 \ln 2$

Mà $\int_{3}^{4} \frac{x + 1}{x - 2} d x = a + b \ln 2$

Þ a = 1, b = 3

Vậy S = 2a + b = 2.1 + 3 = 5.

Câu 18:

Biết $\int (x + 2) \cos 3 x d x = \frac{(x + m) \sin 3 x}{n} + \frac{\cos 3 x}{p} + C$ với m, n, p Î ℤ. Tính T = m + n - p.

A. T = -3;

B. T = 8;

C. T = 10;

D. T = -4.

Xem đáp án

Đáp án đúng là: D

$\int (x + 2) \cos 3 x d x$

Đặt: $\{\begin{matrix} u = x + 2 \Rightarrow d u = d x \\ d v = \cos 3 x d x \Rightarrow v = \frac{1}{3} \sin 3 x \end{matrix}$

$\Rightarrow \int (x + 2) \cos 3 x d x = \frac{x + 2}{3} . \sin 3 x - \int \frac{1}{3} \sin 3 x d x$

$= \frac{x + 2}{3} . \sin 3 x + \frac{1}{9} \cos 3 x + C$

Mà $\int (x + 2) \cos 3 x d x = \frac{(x + m) \sin 3 x}{n} + \frac{\cos 3 x}{p} + C$

Þ m = 2, n = 3, p = 9

Vậy T = m + n - p = 2 + 3 - 9 = -4.

Câu 19:

Diện tích S của hình phẳng giới hạn bởi đồ thị hàm số

y = \frac{2}{{(x + 1)}^{2}},

trục hoành và hai đường thẳng x = 0, x = 4 là:

A. $S = \frac{5}{8};$

B. $S = \frac{8}{5};$

C. $S = \frac{2}{25};$

D. $S = \frac{4}{25} .$

Xem đáp án

Đáp án đúng là: B

Ta có:

$S = \int_{0}^{4} |\frac{2}{{(x + 1)}^{2}}| d x = \int_{0}^{4} \frac{2}{{(x + 1)}^{2}} d x$

$= {- \frac{2}{x + 1}|}_{0}^{4} = - \frac{2}{5} + 2 = \frac{8}{5} .$

Câu 20:

Cho hàm số f (x) có đạo hàm và liên tục trên ℝ thỏa mãn f (x³ + 1) = x + 1. Tính

I = \int_{1}^{9} f (x) d x

A. I = 48;

B. I = 6;

C. I = 20;

D. I = 16.

Xem đáp án

Đáp án đúng là: C

f (x³ + 1) = x + 1

Þ 3x².f (x³ + 1) = 3x².(x + 1) = 3x³ + 3x²

Xét $\int_{0}^{2} 3 x^{2} . f (x^{3} + 1) d x = \int_{0}^{2} (3 x^{3} + 3 x^{2}) d x$

$= {(\frac{3}{4} . x^{4} + x^{3})|}_{0}^{2} = \frac{3}{4} {.2}^{4} + 2^{3} = 20$

Ta có đặt: u = x³ + 1 Þ du = 3x² dx

Đổi cận:

+) x = 0 Þ u = 1

+) x = 2 Þ u = 9

Vậy suy ra

$\int_{0}^{2} 3 x^{2} . f (x^{3} + 1) d x = \int_{1}^{9} f (u) d u = \int_{1}^{9} f (x) d x$

$\Rightarrow I = \int_{1}^{9} f (x) d x = 20.$

Câu 21:

Trong không gian Oxyz, phương trình của đường thẳng d đi qua điểm A(-2; 5; -3) và có vectơ chỉ phương $\vec{u} = (2; 1; - 2)$ là:

A. $d : \{\begin{matrix} x = 2 - 2 t \\ y = 1 + 5 t \\ z = - 2 - 3 t \end{matrix};$

B. $d : \{\begin{matrix} x = - 2 + 2 t \\ y = 5 + t \\ z = - 3 - 2 t \end{matrix};$

C. $d : \{\begin{matrix} x = - 2 + 2 t \\ y = - 1 + 5 t \\ z = 2 - 3 t \end{matrix};$

D. $d : \{\begin{matrix} x = 2 + 2 t \\ y = - 5 + t \\ z = 3 - 2 t \end{matrix} .$

Xem đáp án

Đáp án đúng là: B

Trong không gian Oxyz, phương trình của đường thẳng d đi qua điểm A(-2; 5; -3) và có vectơ chỉ phương $\vec{u} = (2; 1; - 2)$ là:

$d : \{\begin{matrix} x = - 2 + 2 t \\ y = 5 + t \\ z = - 3 - 2 t \end{matrix} .$

Câu 22:

Biết $\int_{1}^{2} (4 x + 3) \ln x d x = a + b \ln 2$ với a, b Î ℤ. Tính S = a + 2b.

A. S = 3;

B. S = 2;

C. S = 34;

D. S = 22.

Xem đáp án

Đáp án đúng là: D

$\int_{1}^{2} (4 x + 3) \ln x d x$

Đặt $\{\begin{matrix} u = \ln x \Rightarrow d u = \frac{1}{x} d x \\ d v = (4 x + 3) d x \Rightarrow v = 2 x^{2} + 3 x \end{matrix}$

$\Rightarrow \int_{1}^{2} (4 x + 3) \ln x d x$

$= {(2 x^{2} + 3 x) . \ln x|}_{1}^{2} - \int_{1}^{2} (2 x^{2} + 3 x) . \frac{1}{x} d x$

$= {(2 x^{2} + 3 x) . \ln x|}_{1}^{2} - \int_{1}^{2} (2 x + 3) d x$

$= {(2 x^{2} + 3 x) . \ln x|}_{1}^{2} - {(x^{2} + 3 x)|}_{1}^{2}$

= 14.ln 2 - 10 + 4 = 14.ln 2 - 6

Mà $\int_{1}^{2} (4 x + 3) \ln x d x = a + b \ln 2$

Þ a = -6, b = 14

Vậy S = a + 2b = -6 + 2.14 = 22.

Câu 23:

Trong không gian Oxyz, tâm của mặt cầu (S): (x + 3)² + (y + 1)² + (z - 1)² = 2 là:

A. I(3; 1; -1);

B. I(3; -1; 1);

C. I(-3; -1; 1);

D. I(-3; 1; -1).

Xem đáp án

Đáp án đúng là: C

Trong không gian Oxyz, tâm của mặt cầu (S): (x + 3)² + (y + 1)² + (z - 1)² = 2 là:

I(-3; -1; 1).

Câu 24:

Tích các giá trị của k để

\int_{k}^{0} (2 x - 4) d x = 3

là

A. -3;

B. 3;

C. -1;

D. 2.

Xem đáp án

Đáp án đúng là: B

$\int_{k}^{0} (2 x - 4) d x = {(x^{2} - 4 x)|}_{k}^{0}$

= 4k - k² = 3

Þ k²- 4k + 3 = 0

Û k²- 3k - k + 3 = 0

Û k.(k - 3) - (k - 3) = 0

Û (k - 3).(k - 1) = 0

$\Rightarrow [\begin{matrix} k - 3 = 0 \\ k - 1 = 0 \end{matrix} \Leftrightarrow [\begin{matrix} k = 3 \\ k = 1 \end{matrix}$

Vậy tích các giá trị của k là: 3.1 = 3.

Câu 25:

Trong không gian Oxyz, cho hai mặt phẳng (P): x - y + 2z - 1 = 0, (Q): x + 2y - z + 2 = 0. Tính góc giữa hai mặt phẳng (P) và (Q) được kết quả là

A. 120°;

B. 150°;

C. 30°;

D. 60°.

Xem đáp án

Đáp án đúng là: D

Ta có véc-tơ pháp tuyến của hai mặt phẳng (P) và (Q) lần lượt là $\vec{n_{(P)}} = (1; - 1; 2)$ và $\vec{n_{(Q)}} = (1; 2; - 1)$

Áp dụng công thức tính góc giữa hai mặt phẳng ta thấy a là góc giữa hai mặt phẳng (P) và (Q) với

$\cos α = \frac{|\vec{n_{(P)}} . \vec{n_{(Q)}}|}{|\vec{n_{(P)}}| . |\vec{n_{(Q)}}|}$

$= \frac{|1.1 + (- 1) .2 + 2. (- 1)|}{\sqrt{1^{2} + {(- 1)}^{2} + 2^{2}} . \sqrt{1^{2} + 2^{2} + {(- 1)}^{2}}}$

$= \frac{1}{2}$

Vậy suy ra a = 60°.

Câu 26:

Thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường y = 1 - x² , y = 0, x = 0, x = 2 xung quanh trục Ox là:

A. $V = \frac{8 π \sqrt{2}}{3};$

B. V = 2p;

C. $V = \frac{46 π}{15};$

D. $V = \frac{5 π}{2} .$

Xem đáp án

Đáp án đúng là: C

Thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường y = 1 - x² , y = 0, x = 0, x = 2 xung quanh trục Ox là:

$V = π . \int_{0}^{2} {(1 - x^{2})}^{2} d x$

$= π . \int_{0}^{2} (1 - 2 x^{2} + x^{4}) d x$

$= {π . (x - \frac{2 x^{3}}{3} + \frac{x^{5}}{5})|}_{0}^{2}$

$= π . (2 - \frac{{2.2}^{3}}{3} + \frac{2^{5}}{5}) = \frac{46 π}{15} .$

Câu 27:

Trong không gian Oxyz, cho hai vectơ

\vec{u} = (m; - 2; m + 1)

và

\vec{v} = (3; - 2 m - 4; 6)

. Tìm tham số m để hai vectơ đã cho cùng phương.

A. m = 0;

B. m = 1;

C. m = -1;

D. m = -2.

Xem đáp án

Đáp án đúng là: B

Để hai vectơ đã cho cùng phương thì $\vec{u} = k . \vec{v}, (k \in ℤ, k \neq 0)$

$\Rightarrow (m; - 2; m + 1) = k . (3; - 2 m - 4; 6)$

$\Rightarrow \{\begin{matrix} m = 3 k \\ - 2 = - 2 m k - 4 k \\ m + 1 = 6 k \end{matrix} \Leftrightarrow \{\begin{matrix} m - 3 k = 0 \\ m k + 2 k = 1 \\ m - 6 k = - 1 \end{matrix}$

$\Leftrightarrow \{\begin{matrix} m - 3 k = 0 \\ m k + 2 k = 1 \\ 3 k = 1 \end{matrix} \Leftrightarrow \{\begin{matrix} m - 3 k = 0 \\ m k + 2 k = 1 \\ k = \frac{1}{3} \end{matrix}$

$\Leftrightarrow \{\begin{matrix} m = 1 \\ m + 2 = 3 \\ k = \frac{1}{3} \end{matrix} \Leftrightarrow \{\begin{matrix} m = 1 \\ k = \frac{1}{3} \end{matrix}$ (Thỏa mãn)

Vậy m = 1 là giá trị của m thỏa mãn ycbt.

Câu 28:

Thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường y = ln x, y = 0, x = e xung quanh trục Ox là:

A. V = p(e - 1);

B. V = p(e - 2);

C. V = p(e + 1);

D. V = pe.

Xem đáp án

Đáp án đúng là: B

Hoành độ giao điểm của hai đường thẳng y = ln x và y = 0 là nghiệm của phương trình:

ln x = 0

Û x = 1

Thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường y = ln x, y = 0, x = e xung quanh trục Ox là:

$V = π . \int_{1}^{e} \ln^{2} x d x$

Đặt: $\{\begin{matrix} u = \ln^{2} x \Rightarrow d u = \frac{2. \ln x}{x} d x \\ d v = d x \Rightarrow v = x \end{matrix}$

$\Rightarrow V = π . \int_{1}^{e} \ln^{2} x d x = π . [{(\ln^{2} x) . x|}_{1}^{e} - \int_{1}^{e} 2. \ln x d x]$

Xét $I = \int_{1}^{e} 2. \ln x d x$

Đặt: $\{\begin{matrix} u = \ln x \Rightarrow d u = \frac{1}{x} d x \\ d v = 2 d x \Rightarrow v = 2 x \end{matrix}$

$\Rightarrow I = \int_{1}^{e} 2. \ln x d x = {2 x . \ln x|}_{1}^{e} - \int_{1}^{e} 2 d x$

$= {(2 x . \ln x - 2 x)|}_{1}^{e}$

Vậy suy ra

$V = π . [{(\ln^{2} x) . x|}_{1}^{e} - {(2 x . \ln x - 2 x)|}_{1}^{e}]$

= p.(e - 2e + 2e - 2) = p(e - 2).

Câu 29:

Trong không gian Oxyz, mặt phẳng (P): x + 2y - 1 = 0 có một vectơ pháp tuyến là:

A. $\vec{n} (1; 2; 0);$

B. $\vec{n} (1; 2; - 1);$

C. $\vec{n} (1; 0; 2);$

D. $\vec{n} (- 1; 2; - 1) .$

Xem đáp án

Đáp án đúng là: A

Trong không gian Oxyz, mặt phẳng (P): x + 2y - 1 = 0 có một vectơ pháp tuyến là:

$\vec{n} (1; 2; 0) .$

Câu 30:

Cho f (x) liên tục trên ℝ và $\int_{2}^{4} f (x) d x = 18, \int_{2}^{8} f (x) d x = 14.$ Khi đó $\int_{4}^{8} f (x) d x$ bằng:

A. 32;

B. 4;

C. -4;

D. -32.

Xem đáp án

Đáp án đúng là: C

Ta có:

$\int_{4}^{8} f (x) d x = \int_{2}^{8} f (x) d x - \int_{2}^{4} f (x) d x$

$= 14 - 18 = - 4.$

Câu 31:

Gọi z₁, z₂ là hai nghiệm phức của phương trình: z² - z + 1 = 0. Khi đó |z₁| + | z₂| bằng:

A. 1;

B. 2;

C. 0;

D. 4.

Xem đáp án

Đáp án đúng là: B

z² - z + 1 = 0

$\Leftrightarrow z^{2} - 2. z \frac{1}{2} + \frac{1}{4} = - \frac{3}{4}$

$\Leftrightarrow {(z - \frac{1}{2})}^{2} = {(\frac{\sqrt{3} . i}{2})}^{2}$

$\Rightarrow \{\begin{matrix} z - \frac{1}{2} = \frac{\sqrt{3} . i}{2} \\ z - \frac{1}{2} = - \frac{\sqrt{3} . i}{2} \end{matrix} \Leftrightarrow \{\begin{matrix} z = \frac{1 + \sqrt{3} . i}{2} \\ z = \frac{1 - \sqrt{3} . i}{2} \end{matrix}$

Khi đó |z₁| + | z₂| bằng:

$|\frac{1 + \sqrt{3} . i}{2}| + |\frac{1 - \sqrt{3} . i}{2}|$

$= \sqrt{{(\frac{1}{2})}^{2} + {(\frac{\sqrt{3}}{2})}^{2}} + \sqrt{{(\frac{1}{2})}^{2} + {(- \frac{\sqrt{3}}{2})}^{2}}$

= 1 + 1 = 2.

Câu 32:

Trong không gian Oxyz, khoảng cách từ điểm M(-1; 2; -4) đến mặt phẳng (P): 2x - 2y + z - 8 = 0 là:

A. $d (M, (P)) = \frac{10}{3};$

B. $d (M, (P)) = - \frac{10}{3};$

C. $d (M, (P)) = - 6;$

D. $d (M, (P)) = 6.$

Xem đáp án

Đáp án đúng là: D

Trong không gian Oxyz, khoảng cách từ điểm M(-1; 2; -4) đến mặt phẳng (P): 2x - 2y + z - 8 = 0 là:

$d_{(M, (P))} = \frac{|2 x_{M} - 2 y_{M} + z_{M} - 8|}{\sqrt{2^{2} + {(- 2)}^{2} + 1^{2}}}$

$= \frac{|2. (- 1) - 2.2 + (- 4) - 8|}{\sqrt{2^{2} + {(- 2)}^{2} + 1^{2}}} = 6.$

Câu 33:

Diện tích S của hình phẳng giới hạn bởi đồ thị các hàm số y = x³ - 3x và y = x là:

A. S = 8;

B. S = 6;

C. S = 4;

D. S = 3.

Xem đáp án

Đáp án đúng là: A

Hoành độ giao điểm của hai đường thẳng y = x³ - 3x và y = x là nghiệm của phương trình:

x³ - 3x = x

Û x³ - 4x = 0

Û x.(x - 2).(x + 2) = 0

$\Rightarrow [\begin{matrix} x = 0 \\ x - 2 = 0 \\ x + 2 = 0 \end{matrix} \Leftrightarrow [\begin{matrix} x = 0 \\ x = 2 \\ x = - 2 \end{matrix}$

Diện tích S của hình phẳng giới hạn bởi đồ thị các hàm số y = x³ - 3x và y = x là:

$S = \int_{- 2}^{2} |x^{3} - 3 x - x| d x = \int_{- 2}^{2} |x^{3} - 4 x| d x$

$= \int_{- 2}^{0} |x^{3} - 4 x| d x + \int_{0}^{2} |x^{3} - 4 x| d x$

$= \int_{- 2}^{0} (x^{3} - 4 x) d x + \int_{0}^{2} (- x^{3} + 4 x) d x$

$= {(\frac{x^{4}}{4} - 2 x^{2})|}_{- 2}^{0} + {(- \frac{x^{4}}{4} + 2 x^{2})|}_{0}^{2}$

= 4 + 4 = 8.

Câu 34:

Trong không gian Oxyz, cho hình bình hành ABCD có đỉnh A(-1; 4; 1), phương trình đường chéo $B D : \frac{x - 2}{1} = \frac{y - 2}{- 1} = \frac{z + 3}{- 2}$ , đỉnh C(a; b; c) thuộc mặt phẳng (P): x + 2y + z - 4 = 0. Khi đó giá trị của S = a + b + c là:

A. S = -2;

B. S = 2;

C. S = 6;

D. S = -6.

Xem đáp án

Đáp án đúng là: B

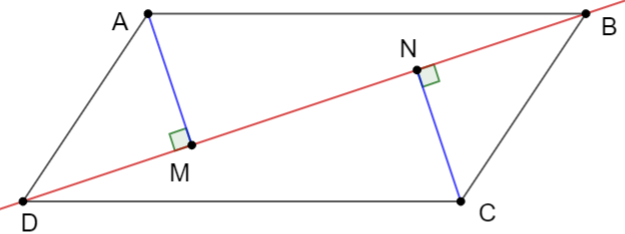
Ta có:

+) $B D : \frac{x - 2}{1} = \frac{y - 2}{- 1} = \frac{z + 3}{- 2}$

$\Rightarrow \{\begin{matrix} x = 2 + t \\ y = 2 - t \\ z = - 3 - 2 t \end{matrix}$

+) Đỉnh C(a; b; c) thuộc mặt phẳng (P): x + 2y + z - 4 = 0

Þ a + 2b + c - 4 = 0 (1)

+) $\vec{u_{B D}} = (1; - 1; - 2)$

Mặt phẳng (Q) vuông góc với BD nhận véc-tơ chỉ phương của đường thẳng BD làm véc-tơ pháp tuyến và đi qua A(-1; 4; 1) có phương trình

(Q): (x + 1) - (y - 4) - 2.(z - 1) = 0

Û x - y - 2z + 7 = 0

M là giao của mặt phẳng (Q) và đường thẳng BD nên ta có M(2 + m; 2 - m; -3 - 2m) Î (Q)

Þ (2 + m) - (2 - m) - 2.(-3 - 2m) + 7 = 0

Û 2 + m - 2 + m + 6 + 4m + 7 = 0

Û 6m + 13 = 0

$\Leftrightarrow m = - \frac{13}{6} \Rightarrow M (- \frac{1}{6}; \frac{25}{6}; \frac{4}{3})$

Kẻ CN ^ BD. Dễ dàng chứng minh được $\vec{A M} = \vec{N C}$

$\Leftrightarrow (\frac{5}{6}; \frac{1}{6}; \frac{1}{3}) = (a - x_{N}; b - y_{N}; c - z_{N})$

$\Rightarrow N (a - \frac{5}{6}; b - \frac{1}{6}; c - \frac{1}{3})$

Mà điểm N Î BD nên suy ra

$\Rightarrow \{\begin{matrix} a - \frac{5}{6} = 2 + t \\ b - \frac{1}{6} = 2 - t \\ c - \frac{1}{3} = - 3 - 2 t \end{matrix} \Leftrightarrow \{\begin{matrix} a = \frac{17}{6} + t \\ b = \frac{13}{6} - t \\ c = \frac{- 8}{3} - 2 t \end{matrix}$ (2)

Thay (2) vào (1) ta được

$(\frac{17}{6} + t) + 2. (\frac{13}{6} - t) + (\frac{- 8}{3} - 2 t) - 4 = 0$

$\Leftrightarrow 3 t - \frac{1}{2} = 0 \Leftrightarrow t = \frac{1}{6}$ (3)

Lại tiếp tục thay (3) vào (2) ta được

$\{\begin{matrix} a = \frac{17}{6} + t = \frac{17}{6} + \frac{1}{6} = 3 \\ b = \frac{13}{6} - t = \frac{13}{6} - \frac{1}{6} = 2 \\ c = \frac{- 8}{3} - 2 t = \frac{- 8}{3} - \frac{1}{3} = - 3 \end{matrix}$

Khi đó giá trị của S = a + b + c là:

S = 3 + 2 - 3 = 2.

Câu 35:

Biết tập hợp điểm biểu diễn số phức z thỏa mãn |z + 2| = |i - z| là đường thẳng d. Khi đó khoảng cách từ gốc tọa độ O đến đường thẳng d bằng:

A. $\frac{3 \sqrt{5}}{2};$

B. $\frac{3 \sqrt{5}}{5};$

C. $\frac{3 \sqrt{5}}{10};$

D. $\frac{3 \sqrt{5}}{20} .$

Xem đáp án

Đáp án đúng là: C

Đặt z = x + yi

Nên suy ra |z + 2| = |i - z|

Û |x + yi + 2| = |i - x - yi|

Û |(x + 2) + yi| = |- x + (1 - y).i|

$\Leftrightarrow \sqrt{{(x + 2)}^{2} + y^{2}} = \sqrt{{(- x)}^{2} + {(1 - y)}^{2}}$

$\Leftrightarrow \sqrt{x^{2} + 4 x + 4 + y^{2}} = \sqrt{x^{2} + y^{2} - 2 y + 1}$

Bình phương 2 vế của phương trình trên ta được

x² + 4x + 4 + y² = x² + y² - 2y + 1

Û 4x + 2y + 3 = 0

Vậy đường thẳng đó là d: 4x + 2y + 3 = 0

Ta có khoảng cách từ O đến d là

$d_{(O, d)} = \frac{|4. x_{O} + 2 y_{O} + 3|}{\sqrt{4^{2} + 2^{2}}} = \frac{3}{2 \sqrt{5}} = \frac{3 \sqrt{5}}{10} .$

Câu 36:

Trong không gian Oxyz, điểm nào sau đây thuộc đường thẳng $d : \frac{x + 2}{1} = \frac{y - 1}{1} = \frac{z + 2}{2}$

A. A(-2; 1; -2);

B. M(2; -1; 2);

C. E(-2; -2; 1);

D. P(1; 1; 2).

Xem đáp án

Đáp án đúng là: A

$d : \frac{x + 2}{1} = \frac{y - 1}{1} = \frac{z + 2}{2}$ (1)

Thay lần lượt các tọa độ của các điểm A, M, E, P vào (1) ta thấy (1) thõa mãn khi tọa độ điểm đó là điểm A có:

$\frac{x_{A} + 2}{1} = \frac{y_{A} - 1}{1} = \frac{z_{A} + 2}{2} = 0$

Câu 37:

Diện tích S của hình phẳng giới hạn bởi đồ thị các hàm số y = x² - 2x +1, y = x + 1, x = 0 và x = m (0 < m < 3) là:

A. $S = \frac{m^{3}}{3} - \frac{3 m^{2}}{2};$

B. $S = \frac{m^{3}}{3} - \frac{m^{2}}{2};$

C. $S = - \frac{m^{3}}{3} + \frac{3 m^{2}}{2};$

D. $S = - \frac{m^{3}}{3} + \frac{m^{2}}{2} .$

Xem đáp án

Đáp án đúng là: C

Diện tích S của hình phẳng giới hạn bởi đồ thị các hàm số y = x² - 2x +1, y = x + 1, x = 0 và x = m (0 < m < 3) là:

$S = \int_{0}^{m} |(x^{2} - 2 x + 1) - (x + 1)| d x = \int_{0}^{m} |x^{2} - 3 x| d x$

$= \int_{0}^{m} (- x^{2} + 3 x) d x = {(- \frac{x^{3}}{3} + \frac{3 x^{2}}{2})|}_{0}^{m}$

$= - \frac{m^{3}}{3} + \frac{3 m^{2}}{2} .$

Câu 38:

Số phức z = 3 - i có phần ảo là:

A. 1;

B. i;

C. -1;

D. -i.

Xem đáp án

Đáp án đúng là: C

Số phức z = 3 - i có phần ảo là: b = -1.

Câu 39:

Thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường $y = \sqrt{1 - x}$ , y = 0, x = 0 xung quanh trục Ox được tính theo công thức nào sau đây?

A. $V = π \int_{0}^{1} (1 - x) d x;$

B. $V = \int_{0}^{1} (1 - x) d x;$

C. $V = π \int_{0}^{1} {(1 - x)}^{2} d x;$

D. $V = \int_{0}^{1} {(1 - x)}^{2} d x .$

Xem đáp án

Đáp án đúng là: A

Thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường $y = \sqrt{1 - x}$ , y = 0, x = 0 xung quanh trục Ox được tính theo công thức:

$V = π \int_{0}^{1} \sqrt{{(1 - x)}^{2}} d x = π \int_{0}^{1} |1 - x| d x$

$= π \int_{0}^{1} (1 - x) d x .$

Câu 40:

Cho số phức z thỏa mãn $z + 2 \bar{z} = 3 + i .$ Phần thực của z bằng:

A. -3;

B. 3;

C. -1;

D. 1.

Xem đáp án

Đáp án đúng là: D

Đặt z = a + bi. Suy ra $\bar{z} = a - b i$

Từ đó: $z + 2 \bar{z} = 3 + i$

Û (a + bi) + 2.(a - bi) = 3 + i

Û a + bi + 2a - 2bi = 3 + i

Û 3a - 2bi = 3 + i

$\Rightarrow \{\begin{matrix} 3 a = 3 \\ - 2 b i = i \end{matrix} \Leftrightarrow \{\begin{matrix} a = 1 \\ b = - \frac{1}{2} \end{matrix}$

Vậy suy ra phần thực của z là a = 1.

Câu 41:

Cho tích phân

I = \int_{0}^{\frac{π}{2}} \sin x \sqrt{8 + \cos x} d x

. Nếu đặt t = 8 + cos x thì kết quả nào đúng?

A. $I = \int_{8}^{9} \sqrt{t} d t;$

B. $I = \int_{9}^{8} \sqrt{t} d t;$

C. $I = \int_{0}^{\frac{π}{2}} \sqrt{t} d t;$

D. $I = - \int_{0}^{\frac{π}{2}} \sqrt{t} d t .$

Xem đáp án

Đáp án đúng là: A

$I = \int_{0}^{\frac{π}{2}} \sin x \sqrt{8 + \cos x} d x$

Đặt t = 8 + cos x

Þ dt = - sin x dx

Đổi cận

+) x = 0 Þ t = 9

+) $x = \frac{π}{2} \Rightarrow t = 8$

Vậy suy ra

$I = \int_{0}^{\frac{π}{2}} \sin x \sqrt{8 + \cos x} d x$

$= \int_{9}^{8} - \sqrt{t} d t = \int_{8}^{9} \sqrt{t} d t .$

Câu 42:

Trong không gian Oxyz, cho mặt phẳng (P): 2x - y + 2z - 4 = 0. Mặt phẳng nào sau đây vuông góc với (P)?

A. x - 4y + z - 2 = 0;

B. x + 4y + z - 1 = 0;

C. x + 4y - z - 2 = 0;

D. - x + 4y + z - 2 = 0.

Xem đáp án

Đáp án đúng là: B

Mặt phẳng (P) có phương trình là: 2x - y + 2z - 4 = 0

Nên véc-tơ pháp tuyến của (P) là $\vec{n_{(P)}} = (2; - 1; 2)$

Ta có các phương án A, B, C, D

+) Phương án A: x - 4y + z - 2 = 0 nên véc-tơ pháp tuyến của mặt phẳng này là $\vec{n_{A}} = (1; - 4; 1)$

+) Phương án B: x + 4y + z - 1 = 0 nên véc-tơ pháp tuyến của mặt phẳng này là $\vec{n_{B}} = (1; 4; 1)$

+) Phương án C: x + 4y - z - 2 = 0 nên véc-tơ pháp tuyến của mặt phẳng này là $\vec{n_{C}} = (1; 4; - 1)$

+) Phương án D: - x + 4y + z - 2 = 0 nên véc-tơ pháp tuyến của mặt phẳng này là $\vec{n_{D}} = (- 1; 4; 1)$

Xét các tích vô hướng:

+) $\vec{n_{(P)}} . \vec{n_{A}} = (2; - 1; 2) . (1; - 4; 1)$

$= 2.1 + (- 1) . (- 4) + 2.1 = 8$

+) $\vec{n_{(P)}} . \vec{n_{B}} = (2; - 1; 2) . (1; 4; 1)$

$= 2.1 + (- 1) .4 + 2.1 = 0$

Nên suy ra $\vec{n_{(P)}} ⊥ \vec{n_{B}}$ . Từ đó suy ra mặt phẳng này vuông góc với mặt phẳng (P)

+) $\vec{n_{(P)}} . \vec{n_{C}} = (2; - 1; 2) . (1; 4; - 1)$

$= 2.1 + (- 1) .4 + 2. (- 1) = - 4$

+) $\vec{n_{(P)}} . \vec{n_{D}} = (2; - 1; 2) . (- 1; 4; 1)$

$= 2. (- 1) + (- 1) .4 + 2.1 = - 4.$

Câu 43:

Biết hàm số f (x) có đạo hàm $f^{'} (x)$ liên tục trên ℝ và f (4) = 2, f (1) = 5. Tính $I = \int_{1}^{4} f^{'} (x) d x .$ .

A. I = -3;

B. I = 3;

C. I = 7;

D. I = 10.

Xem đáp án

Đáp án đúng là: A

Vì hàm số f (x) có đạo hàm liên tục trên ℝ nên ta có

$I = \int_{1}^{4} f^{'} (x) d x = {f (x)|}_{1}^{4}$

= f (4) - f (1) = 2 - 5 = -3.

Câu 44:

Biết F(x) là một nguyên hàm của hàm số $f (x) = \frac{1}{2 x + 1}$ và F (0) = 2. Khi đó F (e) bằng:

A. ln (2e + 1) + 2;

B. $\ln \sqrt{2 e + 1} + 2;$

C. $\frac{1}{2} \ln (2 e + 1);$

D. $\frac{1}{2} \ln (2 e + 1) - 2.$

Xem đáp án

Đáp án đúng là: B

$f (x) = \frac{1}{2 x + 1}$

$\Rightarrow F (x) = \int f (x) d x = \int \frac{1}{2 x + 1} d x$

$= \frac{1}{2} . \int \frac{2}{2 x + 1} d x = \frac{\ln (2 x + 1)}{2} + C$

Mà F (0) = 2 Þ C = 2

Vậy suy ra $F (x) = \frac{\ln (2 x + 1)}{2} + 2$

Khi đó $F (e) = \frac{\ln (2 e + 1)}{2} + 2 = \ln \sqrt{2 e + 1} + 2.$

Câu 45:

Trong không gian Oxyz, bán kính của mặt cầu (S): x² + y² + z² + 2x - 4y + 6z - 2 = 0 là:

A. R = 16;

B. R = 23;

C. R = 12;

D. R = 4.

Xem đáp án

Đáp án đúng là: D

Ta có:

(S): x² + y² + z² + 2x - 4y + 6z - 2 = 0

Û (x² + 2x + 1) + (y² - 4y + 4) + (z² + 6z + 9) = 16

Û (x + 1)² + (y - 2)² + (z + 3)² = 16 = 4²

Vậy suy ra bán kính của mặt cầu (S) là R = 4.

Câu 46:

Biết $\int_{1}^{2} \frac{x^{2} + x + 1}{x + 1} d x = a + \ln b$ ; a, b Î ℝ. Khẳng định nào đúng?

A. a > 2b;

B. a < b;

C. a = b;

D. 2a - b + b² = 0.

Xem đáp án

Đáp án đúng là: C

$\int_{1}^{2} \frac{x^{2} + x + 1}{x + 1} d x = \int_{1}^{2} \frac{x (x + 1) + 1}{x + 1} d x$

$= \int_{1}^{2} (x + \frac{1}{x + 1}) d x = {[\frac{x^{2}}{2} + \ln (x + 1)]|}_{1}^{2}$

$= 2 + \ln 3 - \frac{1}{2} - \ln 2 = \frac{3}{2} + \ln \frac{3}{2}$

Mà $\int_{1}^{2} \frac{x^{2} + x + 1}{x + 1} d x = a + \ln b$

Nên suy ra $a = b = \frac{3}{2} .$

Câu 47:

Trong không gian Oxyz, cho bốn điểm A(2; -1; 6), B(-3; -1; -4), C(5; -1; 0), D(1; 2; 1). Thể tích của tứ diện ABCD là:

A. V = 60;

B. V = 40;

C. V = 30;

D. V = 10;

Xem đáp án

Đáp án đúng là: C

Ta có:

$+) \vec{A B} = (- 5; 0; - 10)$

$+) \vec{A C} = (3; 0; - 6)$

$+) \vec{A D} = (- 1; 3; - 5)$

Áp dụng công thức tính thể tích tứ diện trong không gian ta có

$V_{A . B C D} = \frac{1}{6} . |[\vec{A B}, \vec{A C}] . \vec{A D}|$

$= \frac{1}{6} |(|\begin{matrix} 0 & - 10 \\ 0 & - 6 \end{matrix}|; |\begin{matrix} - 10 & - 5 \\ - 6 & 3 \end{matrix}|; |\begin{matrix} - 5 & 0 \\ 3 & 0 \end{matrix}|) . (- 1; 3; - 5)|$

$= \frac{1}{6} |(0; - 60; 0) . (- 1; 3; - 5)|$

$= \frac{1}{6} |(0; - 180; 0)| = \frac{1}{6} .180 = 30.$

Câu 48:

Trong không gian Oxyz, mặt phẳng đi qua điểm M(3, 4, 5) và nhận $\vec{n} = (1; - 3; - 7)$ làm vectơ pháp tuyến có phương trình là:

A. x - 3y - 7z + 20 = 0;

B. x - 3y - 7z - 44 = 0;

C. 3x + 4y + 5z + 44 = 0;

D. x - 3y - 7z + 44 = 0.

Xem đáp án

Đáp án đúng là: D

Trong không gian Oxyz, mặt phẳng đi qua điểm M(3, 4, 5) và nhận $\vec{n} = (1; - 3; - 7)$ làm vectơ pháp tuyến có phương trình là:

(x - 3) - 3.(y - 4) - 7.(z - 5) = 0

Û x - 3 - 3y + 12 - 7z + 35 = 0

Û x - 3y - 7z + 44 = 0.

Câu 49:

Cho số phức z = 7 + 2i. Trong mặt phẳng Oxy điểm biểu diễn số phức có tọa độ là:

A. (7; 2);

B. (7; -2);

C. (-7; -2);

D. (-7; 2).

Xem đáp án

Đáp án đúng là: B

Với số phức z = 7 + 2i $\Rightarrow \bar{z} = 7 - 2 i$

Trong mặt phẳng Oxy điểm biểu diễn số phức có tọa độ là:

M(7; -2).

Câu 50:

Trên mặt phẳng Oxy, gọi A, B, C lần lượt là các điểm biểu diễn các số phức $z_{1} = \frac{4 i}{i - 1}, z_{2} = (1 - i) (1 + 2 i), z_{3} = - 2 i^{3} .$ Khi đó tam giác ABC là:

A. Tam giác đều B;

B. Tam giác vuông tại C;

C. Tam giác vuông tại A;

D. Tam giác vuông tại B.

Xem đáp án

Đáp án đúng là: D

Từ đó suy ra AB² + CB² = AC²

Theo định lý Pytago đảo nên tam giác ABC vuông tại B.

A, B, C lần lượt là các điểm biểu diễn các số phức $z_{1} = \frac{4 i}{i - 1}, z_{2} = (1 - i) (1 + 2 i),$ $z_{3} = - 2 i^{3} .$

Nên ta có:

$+) z_{1} = \frac{4 i}{i - 1} = \frac{4 i (- i - 1)}{(i - 1) . (- i - 1)}$

$= \frac{4 - 4 i}{2} = 2 - 2 i$

Þ A(2; -2)

+) z₂ = (1 - i)(1 + 2i) = 1 - i + 2i - 2i²

= 3 + i

Þ B(3; 1)

+) z₃ = -2i³ = 2i

Þ C(0; 2)

Từ đó ta có:

$+) A B = \sqrt{{(3 - 2)}^{2} + {(1 + 2)}^{2}} = \sqrt{10}$

$+) A C = \sqrt{{(0 - 2)}^{2} + {(2 + 2)}^{2}} = 2 \sqrt{5}$

$+) C B = \sqrt{{(3 - 0)}^{2} + {(1 - 2)}^{2}} = \sqrt{10}$

Từ đó suy ra AB² + CB² = AC²

Theo định lý Pytago đảo nên tam giác ABC vuông tại B.

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đề kiểm tra Học kì 2 Toán 12 có đáp án (Mới nhất)

Đề kiểm tra Học kì 2 Toán 12 có đáp án (Mới nhất) - Đề 10

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương