50 câu hỏi trắc nghiệm thuộc Đề kiểm tra Học kì 2 Toán 12 có đáp án (Mới nhất) - Đề 13

Câu 1:

Số phức liên hợp của z thỏa mãn 3z = 3 + 6i là:

A. $\bar{z} = 1 + 2 i;$

B. $\bar{z} = - 1 - 2 i;$

C. $\bar{z} = 1 - 2 i;$

D. $\bar{z} = - 1 + 2 i .$

Xem đáp án

Đáp án đúng là: C

3z = 3 + 6i

Û z = 1 + 2i

Vậy suy ra số phức liên hợp của z là $\bar{z} = 1 - 2 i .$

Câu 2:

Cho hàm số y = f (x) liên tục trên đoạn [a; b]. Gọi D là hình phẳng giới hạn bởi đồ thị hàm số y = f (x), trục hoành và hai đường thẳng x = a, x = b (a < b). Thể tích của khối tròn xoay tạo thành khi quay D quanh trục hoành được tính theo công thức:

A. $V = 2 π \int_{a}^{b} f^{2} (x) d x;$

B. $V = π \int_{a}^{b} f^{2} (x) d x;$

C. $V = π \int_{a}^{b} f (x) d x;$

D. $V = \int_{a}^{b} f^{2} (x) d x .$

Xem đáp án

Đáp án đúng là: B

Thể tích của khối tròn xoay tạo thành khi quay D quanh trục hoành được tính theo công thức:

$V = π \int_{a}^{b} f^{2} (x) d x .$

Câu 3:

Cho hàm số f (x) liên tục trên [a; b] và F (x) là một nguyên hàm của f (x). Tìm khẳng định sai.

A. $\int_{a}^{b} f (x) d x = F (b) - F (a);$

B. $\int_{a}^{b} f (x) d x = F (a) - F (b);$

C. $\int_{a}^{a} f (x) d x = 0;$

D. $\int_{a}^{b} f (x) d x = - \int_{b}^{a} f (x) d x .$

Xem đáp án

Đáp án đúng là: B

Cho hàm số f (x) liên tục trên [a; b] và F (x) là một nguyên hàm của f (x)

Xét các mệnh đề:

+) $\int_{a}^{b} f (x) d x = F (b) - F (a)$

Nên suy ra đáp án A đúng

Từ đó suy ra được đáp án B sai

+) $\int_{a}^{a} f (x) d x = 0$

Nên suy ra đáp án C đúng

+) $\int_{a}^{b} f (x) d x = - \int_{b}^{a} f (x) d x$

Nên suy ra án D đúng.

Câu 4:

Cho hàm số y = f (x) xác định và liên tục trên đoạn [a; b]. Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f (x), trục hoành và hai đường thẳng x = a, x = b, được tính theo công thức

A. $S = \int_{b}^{a} |f (x)| d x;$

B. $S = |\int_{a}^{b} f (x) d x|;$

C. $S = \int_{a}^{b} |f (x)| d x;$

D. $S = - \int_{a}^{b} f (x) d x .$

Xem đáp án

Đáp án đúng là: C

Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f (x), trục hoành và hai đường thẳng x = a, x = b, được tính theo công thức:

$S = \int_{a}^{b} |f (x)| d x .$

Câu 5:

Phương trình nào sau đây là phương trình bậc hai với hệ số thực?

A. 2z + 3 = 0;

B. iz² + 3z = 0;

C. z² + 3z + 1 = 0;

D. z² + iz + 2 = 0.

Xem đáp án

Đáp án đúng là: C

+) 2z + 3 = 0

Đây là phương trình bậc nhất với hệ số thực

+) iz² + 3z = 0

Đây là phương tình bậc hai với hệ số không là số thực

+) z² + 3z + 1 = 0

Đây là phương trình bậc hai với hệ số thực

+) z² + iz + 2 = 0

Đây là phương tình bậc hai với hệ số không là số thực.

Câu 6:

$\int x^{3} d x$ bằng

A. x⁴ + C;

B. $\frac{1}{4} x^{4} + C;$

C. 3x² + C;

D. x⁴.

Xem đáp án

Đáp án đúng là: B

$\int x^{3} d x = \frac{1}{4} \int 4 x^{3} d x = \frac{1}{4} x^{4} + C .$

Câu 7:

Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(1; 0; 2) và B(4; 1; 1) Vectơ $\vec{A B}$ có tọa độ là:

A. (-3; -1; 1);

B. (3; 1; 1);

C. (3; -1; -1);

D. (3; 1; -1).

Xem đáp án

Đáp án đúng là: D

Vectơ $\vec{A B}$ có tọa độ là:

$\vec{A B} = (4 - 1; 1 - 0; 1 - 2) = (3; 1; - 1) .$

Câu 8:

Cho hai số phức z₁ = 3 + i và z₂ = 3 - i. Tính tích z₁z₂

A. 10;

B. 7;

C. 6;

D. 8.

Xem đáp án

Đáp án đúng là: A

z₁z₂ = (3 + i)(3 - i) = 3² + 1² = 10.

Câu 9:

Trong không gian Oxyz, cho mặt phẳng (P) có phương trình 3x + 2y + z + 1 = 0. Tìm một vectơ pháp tuyến của (P).

A. $\vec{n} = (3; 2; 0);$

B. $\vec{n} = (3; 2; 1);$

C. $\vec{n} = (- 2; 3; 1);$

D. $\vec{n} = (3; - 2; - 1) .$

Xem đáp án

Đáp án đúng là: B

Mặt phẳng (P) có phương trình 3x + 2y + z + 1 = 0 có một vectơ pháp tuyến là $\vec{n} = (3; 2; 1) .$

Câu 10:

Trong không gian với hệ tọa độ Oxyz, cho $\vec{a} = - 2 \vec{i} + 3 \vec{j} + \vec{k}$ . Tọa độ của $\vec{a}$ là

A. $\vec{a} = (- 2; 3; 0);$

B. $\vec{a} = (2; - 3; - 1);$

C. $\vec{a} = (- 2 \vec{i}; 3 \vec{j}; 1 \vec{k});$

D. $\vec{a} = (- 2; 3; 1) .$

Xem đáp án

Đáp án đúng là: D

$\vec{a} = - 2 \vec{i} + 3 \vec{j} + \vec{k}$

Nên suy ra tọa độ véc-tơ $\vec{a}$ là $\vec{a} = (- 2; 3; 1) .$

Câu 11:

Số phức 6 + 5i có phần thực bằng:

A. -6;

B. 5;

C. -5;

D. 6.

Xem đáp án

Đáp án đúng là: D

Số phức 6 + 5i có phần thực bằng: 6.

Câu 12:

Cho hai số phức z₁ = 1 - 3i và z₂ = 4 + 2i. Số phức z₁ - z₂ bằng

A. -3 + 5i;

B. 4 + i;

C. 3 + 5i;

D. -3 - 5i.

Xem đáp án

Đáp án đúng là: D

z₁ - z₂ = (1 - 3i) - (4 + 2i)

= 1 - 3i - 4 - 2i = -3 - 5i.

Câu 13:

Trong không gian Oxyz, cho đường thẳng ∆ có phương trình chính tắc $\frac{x - 2}{2} = \frac{y - 3}{- 3} = \frac{z}{1}$ . Một véc tơ chỉ phương của đường thẳng ∆ là

A. $\vec{c} = (- 2; 3; 0);$

B. $\vec{b} = (2; 3; 1);$

C. $\vec{a} = (2; - 3; 1);$

D. $\vec{d} = (2; 3; 0) .$

Xem đáp án

Đáp án đúng là: C

Đường thẳng ∆ có phương trình chính tắc $\frac{x - 2}{2} = \frac{y - 3}{- 3} = \frac{z}{1}$ .

Một véc tơ chỉ phương của đường thẳng ∆ là $\vec{a} = (2; - 3; 1) .$

Câu 14:

Số phức $z = \frac{1}{1 - i}$ có tổng phần thực và phần ảo bằng:

A. 1;

B. 0;

C. 2;

D. 3.

Xem đáp án

Đáp án đúng là: A

$z = \frac{1}{1 - i} = \frac{1 + i}{(1 - i) (1 + i)} = \frac{1 + i}{1^{2} + 1^{2}} = \frac{1}{2} + \frac{1}{2} i$

Vậy tổng phần thực và phần ảo của số phức z là $\frac{1}{2} + \frac{1}{2} = 1.$

Câu 15:

Trong không gian Oxyz. Điểm nào sau đây thuộc mặt phẳng (P): -2x + y - 5 = 0?

A. (-2; 1; 0);

B. (-2; 2; 1);

C. (-3; 1; 0);

D. (2; 1; 0).

Xem đáp án

Đáp án đúng là: A

Lần lượt thay tọa độ các điểm ở các phương án A, B, C, D vào phương trình mặt phẳng (P) ta thấy tọa độ của đáp án A thuộc mặt phẳng (P) với

-2x_M + y_M - 5 = -2.(-2) + 1 - 5 = 0.

Câu 16:

Biết tích phân $\int_{0}^{1} f (x) d x = 4$ và $\int_{0}^{1} g (x) d x = - 3$ . Khi đó $\int_{0}^{1} [f (x) - g (x)] d x$ bằng

A. 1;

B. -7;

C. -1;

D. 7.

Xem đáp án

Đáp án đúng là: D

$\int_{0}^{1} [f (x) - g (x)] d x = \int_{0}^{1} f (x) d x - \int_{0}^{1} g (x) d x$

= 4 - (-3) = 7.

Câu 17:

Trong không gian Oxyz, phương trình nào sau đây là phương trình tham số của đường thẳng d qua điểm M (2; 3; 1) và có vectơ chỉ phương $\vec{a} = (1; 2; 2)$ ?

A. $\{\begin{matrix} x = 1 - 2 t \\ y = - 2 + 3 t \\ z = 2 + t \end{matrix};$

B. $\{\begin{matrix} x = 2 + t \\ y = 3 - 2 t \\ z = 1 + 2 t \end{matrix};$

C. $\{\begin{matrix} x = 1 + 2 t \\ y = 2 + 3 t \\ z = 2 + t \end{matrix};$

D. $\{\begin{matrix} x = 2 + t \\ y = 3 + 2 t \\ z = 1 + 2 t \end{matrix} .$

Xem đáp án

Đáp án đúng là: D

Phương trình tham số của đường thẳng d qua điểm M (2; 3; 1) và có vectơ chỉ phương $\vec{a} = (1; 2; 2)$ là

$d : \{\begin{matrix} x = 2 + t \\ y = 3 + 2 t \\ z = 1 + 2 t \end{matrix} .$

Câu 18:

Số phức liên hợp của số phức 1 - 2i là:

A. -1 + 2i;

B. -1 - 2i;

C. 1 + 2i;

D. -2 + i.

Xem đáp án

Đáp án đúng là: C

Số phức liên hợp của số phức 1 - 2i là: 1 + 2i.

Câu 19:

Hàm số F (x) là một nguyên hàm của hàm số f (x) trên khoảng K nếu

A. f '(x) = F (x), "x Î K;

B. F '(x) = -f (x), "x Î K;

C. F '(x) = f (x), "x Î K;

D. f '(x) = -F (x), "x Î K.

Xem đáp án

Đáp án đúng là: C

F (x) là một nguyên hàm của hàm số f (x) trên khoảng K nếu F '(x) = f (x), "x Î K.

Câu 20:

Họ nguyên hàm của hàm số f (x) = 2sin x là

A. -2cos x;

B. -2cos x + C;

C. 2cos x + C;

D. cos 2x + C.

Xem đáp án

Đáp án đúng là: B

Họ nguyên hàm của hàm số f (x) = 2sin x là

$F (x) = \int f (x) d x = \int 2 \sin x d x = - 2 \int - \sin x d x$

= -2cos x + C.

Câu 21:

Trong không gian Oxyz, cho ba điểm M(1; 3; 2), N(-1; 2; 1), P(1; 2; -1). Lập phương trình tham số của đường thẳng đi qua điểm M và song song với NP.

A. $\{\begin{matrix} x = 1 + 2 t \\ y = 3 \\ z = 2 - 2 t \end{matrix};$

B. $\{\begin{matrix} x = 1 \\ y = 3 + 4 t \\ z = 2 \end{matrix};$

C. $\{\begin{matrix} x = 1 - 2 t \\ y = 3 \\ z = 2 - 2 t \end{matrix};$

D. $\{\begin{matrix} x = 1 + 2 t \\ y = 3 \\ z = 2 - 2 t \end{matrix} .$

Xem đáp án

Đáp án đúng là: A + D

Ta có: $\vec{N P} = (2; 0; - 2)$

Phương trình tham số của đường thẳng đi qua điểm M(1; 3; 2) và song song với NP nên nhận $\vec{N P} = (2; 0; - 2)$ làm véc-tơ chỉ phương là

$\{\begin{matrix} x = 1 + 2 t \\ y = 3 \\ z = 2 - 2 t \end{matrix} .$

Câu 22:

Diện tích hình phẳng giới hạn bởi hai đường y = x² + 1 và y = 2x + 1 bằng

A. $\frac{4}{3};$

B. 36;

C. 36p;

D. $\frac{4 π}{3} .$

Xem đáp án

Đáp án đúng là: A

Hoành độ giao điểm của hai đường y = x² + 1 và y = 2x + 1 là nghiệm của phương trình

x² + 1 = 2x + 1

Û x² = 2x

$\Leftrightarrow [\begin{matrix} x = 0 \\ x = 2 \end{matrix}$

Diện tích hình phẳng giới hạn bởi hai đường y = x² + 1 và y = 2x + 1 bằng

$S = \int_{0}^{2} |x^{2} + 1 - 2 x - 1| d x = \int_{0}^{2} |x^{2} - 2 x| d x$

$= - \int_{0}^{2} (x^{2} - 2 x) d x = - {(\frac{x^{3}}{3} - x^{2})|}_{0}^{2}$

$= - (\frac{2^{3}}{3} - 2^{2}) = \frac{4}{3} .$

Câu 23:

Tính tích phân $I = \int_{1}^{2} 2 x \sqrt{x^{2} - 1} d x$ bằng cách đặt $u = \sqrt{x^{2} - 1}$ , mệnh đề nào dưới đây đúng?

A. $I = \int_{0}^{\sqrt{3}} \sqrt{u} d u;$

B. $I = 2 \int_{0}^{3} u d u;$

C. $I = 2 \int_{1}^{2} u d u;$

D. $I = 2 \int_{0}^{\sqrt{3}} u^{2} d u .$

Xem đáp án

Đáp án đúng là: D

$u = \sqrt{x^{2} - 1} \Rightarrow u^{2} = x^{2} - 1$

Þ 2u du = 2x dx

Đổi cận

+) x = 1 Þ u = 0

+)

Nên suy ra

$I = \int_{1}^{2} 2 x \sqrt{x^{2} - 1} d x = \int_{0}^{\sqrt{3}} 2 u . u d u = \int_{0}^{\sqrt{3}} 2 u^{2} d u .$

Câu 24:

Trong không gian Oxyz, cho hai điểm A(1; 0; -1), B(2; 1; -1). Lập phương trình mặt phẳng trung trực của đoạn AB.

A. -x - y + 1 = 0;

B. x - y - 1 = 0;

C. x + y - 2 = 0;

D. x + y + 2 = 0.

Xem đáp án

Đáp án đúng là: C

Gọi I là trung điểm của AB nên suy ra tọa độ trung điểm đoạn thẳng AB là

$\{\begin{matrix} x_{I} = \frac{x_{A} + x_{B}}{2} = \frac{1 + 2}{2} = \frac{3}{2} \\ y_{I} = \frac{y_{A} + y_{B}}{2} = \frac{0 + 1}{2} = \frac{1}{2} \\ z_{I} = \frac{z_{A} + z_{B}}{2} = \frac{- 1 - 1}{2} = - 1 \end{matrix}$

$\Rightarrow I (\frac{3}{2}; \frac{1}{2}; - 1)$

+) $\vec{A B} = (1; 1; 0)$

Phương trình mặt phẳng trung trực của đoạn AB đi qua $I (\frac{3}{2}; \frac{1}{2}; - 1)$ và có véc-tơ pháp tuyến là $\vec{A B} = (1; 1; 0)$

$(x - \frac{3}{2}) + (y - \frac{1}{2}) = 0 \Leftrightarrow x + y - 2 = 0$

Câu 25:

Tìm nguyên hàm của hàm số $f (x) = x^{2} - \frac{2}{x^{2}}$ .

A. $\int f (x) d x = \frac{x^{3}}{3} + \frac{2}{x} + C;$

B. $\int f (x) d x = x^{3} - \frac{2}{x} + C;$

C. $\int f (x) d x = \frac{x^{3}}{3} - \frac{2}{x} + C;$

D. $\int f (x) d x = \frac{x^{3}}{3} - \frac{1}{x} + C .$

Xem đáp án

Đáp án đúng là: A

Nguyên hàm của hàm số $f (x) = x^{2} - \frac{2}{x^{2}}$ là

$\int f (x) d x = \int (x^{2} - \frac{2}{x^{2}}) d x = \frac{x^{3}}{3} + \frac{2}{x} + C .$

Câu 26:

Cho hình phẳng D giới hạn bởi đường cong $y = \sqrt{4 - \sin x}$ , trục hoành và các đường thẳng $x = 0, x = \frac{π}{2}$ . Khối tròn xoay tạo thành khi quay D quay quanh trục hoành có thể tích V bằng bao nhiêu?

A. V = p(2p + 1);

B. V = p(2p - 1);

C. V = 2p - 1;

D. V = 2p + 1;

Xem đáp án

Đáp án đúng là: B

Khối tròn xoay tạo thành khi quay D quay quanh trục hoành có thể tích V bằng

$V = π \int_{0}^{\frac{π}{2}} {\sqrt{4 - \sin x}}^{2} d x = π \int_{0}^{\frac{π}{2}} (4 - \sin x) d x$

$= π {(4 x + \cos x)|}_{0}^{\frac{π}{2}} = π (2 π - 1) .$

Câu 27:

Trong hình vẽ bên, điểm M biểu diễn số phức $\bar{z}$ .

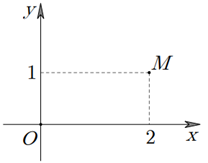
Media VietJack

Số phức z là:

A. 1 - 2i;

B. 1 + 2i;

C. 2 - i;

D. 2 + i.

Xem đáp án

Đáp án đúng là: C

Điểm M biểu diễn số phức $\bar{z}$ nên:

$\bar{z} = 2 + i$

Suy ra số phức z = 2 - i.

Câu 28:

Gọi z₁ và z₂ là hai nghiệm phức của phương trình 3z² - z + 1 = 0. Tính P = |z₁| + |z₂|.

A. $P = \frac{\sqrt{14}}{3};$

B. $P = \frac{2}{3};$

C. $P = \frac{2 \sqrt{3}}{3};$

D. $P = \frac{\sqrt{3}}{3} .$

Xem đáp án

Đáp án đúng là: C

z₁ và z₂ là hai nghiệm phức của phương trình 3z² - z + 1 = 0

Theo định lí Vi-et:

$z_{1} . z_{2} = \frac{1}{3} \Rightarrow |z_{1} . z_{2}| = |z_{1}| . |z_{2}| = \frac{1}{3}$

$\Rightarrow |z_{1}| = |z_{2}| = \sqrt{|z_{1} . z_{2}|} = \sqrt{\frac{1}{3}}$

Vậy suy ra $P = |z_{1}| + |z_{2}| = \sqrt{\frac{1}{3}} + \sqrt{\frac{1}{3}} = \frac{2 \sqrt{3}}{3} .$

Câu 29:

Tìm môđun của số phức z, biết $\frac{1}{z} = \frac{1}{2} - \frac{1}{2} i .$

A. $|z| = \frac{1}{2};$

B. |z| = 2;

C. $|z| = \sqrt{2};$

D. $|z| = \frac{1}{\sqrt{2}} .$

Xem đáp án

Đáp án đúng là: C

$\frac{1}{z} = \frac{1}{2} - \frac{1}{2} i = \frac{1 - i}{2}$

Lấy môđun của 2 vế ta được

$|\frac{1}{z}| = |\frac{1 - i}{2}| \Leftrightarrow \frac{1}{|z|} = \frac{|1 - i|}{2}$

$\Leftrightarrow |z| = \frac{2}{|1 - i|} = \frac{2}{\sqrt{1^{2} + {(- 1)}^{2}}} = \sqrt{2} .$

Câu 30:

Cho số phức z = 2 - 5i. Tìm số phức $w = i z + \bar{z}$ .

A. w = 3 + 7i;

B. w = 7 + 7i;

C. w = -7 - 7i;

D. w = 7 - 3i.

Xem đáp án

Đáp án đúng là: B

z = 2 - 5i $\Rightarrow \bar{z} = 2 + 5 i$

$w = i z + \bar{z} = i (2 - 5 i) + (2 + 5 i)$

= 2i - 5i² + 2 + 5i = 2i + 5 + 2 + 5i

= 7 + 7i.

Câu 31:

Trong không gian Oxyz, cho điểm M(3; 1; -2) và mặt phẳng (a): 3x - y + 2z + 4 = 0. Mặt phẳng (P) đi qua M và song song với (a) có phương trình là

A. 3x + y - 2z - 14 = 0;

B. 3x - y + 2z - 4 = 0;

C. 3x - y - 2z - 6 = 0;

D. 3x - y + 2z + 4 = 0.

Xem đáp án

Đáp án đúng là: B

Mặt phẳng (P) song song với (a) có dạng (P): 3x - y + 2z + m = 0.

Mà điểm M thuộc (P) nên thay tọa độ của M vào phương trình (P) ta có:

3.3 - 1 + 2.(-2) + m = 0 Û m = -4

Vậy suy ra phương trình mặt phẳng (P) là: 3x - y + 2z - 4 = 0.

Câu 32:

Trong mặt phẳng phức Oxy, gọi M là điểm biểu diễn số phức z = 4 - 3i. Tính độ dài đoạn thẳng OM.

A. OM = 25;

B. OM = 5;

C. $O M = \sqrt{7};$

D. $O M = \sqrt{5} .$

Xem đáp án

Đáp án đúng là: B

M là điểm biểu diễn số phức z = 4 - 3i nên suy ra M(4; -3)

Khi đó $O M = \sqrt{4^{2} + {(- 3)}^{2}} = 5.$

Câu 33:

Cho tích phân $\int_{0}^{1} (x - 2) e^{x} d x = a + b e$ , với a; b Î ℤ. Tính a - b.

A. -5;

B. 5;

C. -1;

D. 1.

Xem đáp án

Đáp án đúng là: B

Đặt $\{\begin{matrix} u = x - 2 \Rightarrow d u = d x \\ d v = e^{x} d x \Rightarrow v = e^{x} \end{matrix}$

Suy ra $\int_{0}^{1} (x - 2) e^{x} d x = {(x - 2) e^{x}|}_{0}^{1} - \int_{0}^{1} e^{x} d x$

$= {(x - 2) e^{x}|}_{0}^{1} - {e^{x}|}_{0}^{1} = {(x - 3) e^{x}|}_{0}^{1}$

Khi đó a - b = 3 - (-2) = 5.

Câu 34:

Trong không gian với hệ tọa độ Oxyz, cho hai vectơ

\vec{a} = (- 1; 1; - 2),

\vec{b} = (3; - 3; 6)

. Khẳng định nào sau đây là đúng?

A. $\vec{a} = 3 \vec{b};$

B. $\vec{a} = - 3 \vec{b};$

C. $\vec{b} = 3 \vec{a};$

D. $\vec{b} = - 3 \vec{a} .$

Xem đáp án

Đáp án đúng là: D

Ta có: $\vec{b} = (3; - 3; 6) = ((- 3) . (- 1); (- 3) .1; (- 3) .2)$

$\Leftrightarrow \vec{b} = (3; - 3; 6) = (- 3) (- 1; 1; 2) = - 3 \vec{a} .$

Câu 35:

Trên khoảng $(\frac{5}{3}; + \infty)$ thì $\int \frac{1}{5 - 3 x} d x$ bằng

A. $\frac{- 1}{3} \ln (3 x - 5) + C;$

B. $\frac{1}{5} \ln |5 - 3 x| + C;$

C. ln |5 - 3x| + C;

D. $\frac{1}{3} \ln (5 - 3 x) + C .$

Xem đáp án

Đáp án đúng là: A

$\int \frac{1}{5 - 3 x} d x = - \frac{1}{3} \int \frac{- 3}{5 - 3 x} d x$

$= - \frac{1}{3} \ln |5 - 3 x| + C = - \frac{1}{3} \ln (3 x - 5) + C .$

Câu 36:

Cho $\int_{0}^{1} f (x) d x = 2$ . Giá trị của $\int_{0}^{\frac{π}{4}} f (\cos 2 x) \sin 2 x d x$ bằng

A. -1;

B. 2;

C. -2;

D. 1.

Xem đáp án

Đáp án đúng là: D

Đặt u = cos 2x

Đổi cận

+) x = 0 Þ u = 1

+) $x = \frac{π}{4} \Rightarrow u = 0$

Khi đó $\int_{0}^{\frac{π}{4}} f (\cos 2 x) \sin 2 x d x = \frac{- 1}{2} \int_{1}^{0} f (u) d u$

$= \frac{1}{2} \int_{0}^{1} f (u) d u = \frac{1}{2} .2 = 1.$

Câu 37:

Trong không gian Oxyz, (a) là mặt phẳng đi qua điểm A(2; -1; 5) và vuông góc với hai mặt phẳng (P): 3x - 2y + z = 0 và (Q): 5x - 4y + 3z + 1 = 0. Lập phương trình của mặt phẳng (a).

A. x + 2y - z + 5 = 0;

B. x + 2y + z - 5 = 0;

C. 2x - 4y - 2z - 10 = 0;

D. 2x + 4y + 2z + 10 = 0.

Xem đáp án

Đáp án đúng là: B

Ta có:

+) $\vec{n_{P}} = (3; - 2; 1)$

+) $\vec{n_{Q}} = (5; - 4; 3)$

Mặt phẳng (a) vuông góc với hai mặt phẳng (P) và (Q) nên suy ra $\vec{n_{α}}$ vuông góc với hai véc-tơ $\vec{n_{P}}$ và $\vec{n_{Q}}$

$\Rightarrow \vec{n_{α}} = [\vec{n_{P}}; \vec{n_{Q}}] = (|\begin{matrix} - 2 & 1 \\ - 4 & 3 \end{matrix}|; |\begin{matrix} 1 & 3 \\ 3 & 5 \end{matrix}|; |\begin{matrix} 3 & - 2 \\ 5 & - 4 \end{matrix}|)$

= (-2; -4; -2) = -2(1; 2; 1)

Mặt phẳng (a) đi qua A(2; -1; 5) và nhận (1; 2; 1) làm véc-tơ pháp tuyến là

(a): (x - 2) + 2(y + 1) + (z - 5) = 0

Û x + 2y + z - 5 = 0.

Câu 38:

Cho hàm số f (x) liên tục trên ℝ và f (3) = 12, $\int_{0}^{3} f (x) d x = 9$ . Tính $I = \int_{0}^{1} x . f' (3 x) d x$ .

A. 21;

B. 3;

C. 9;

D. 27.

Xem đáp án

Đáp án đúng là: B

Đặt $\{\begin{matrix} u = x \Rightarrow d u = d x \\ d v = f^{'} (3 x) d x \Rightarrow v = \frac{1}{3} f (3 x) \end{matrix}$

Nên suy ra

$I = \int_{0}^{1} x . f' (3 x) d x = {\frac{x}{3} f (3 x)|}_{0}^{1} - \frac{1}{3} \int_{0}^{1} f (3 x) d x$

Đặt u = 3x Þ du = 3 dx

Đổi cận:

+) x = 0 Þ u = 0

+) x = 1 Þ u = 3

Từ đó suy ra (1) trở thành

$I = {\frac{x}{3} f (3 x)|}_{0}^{1} - \frac{1}{9} \int_{0}^{3} f (u) d u$

$= \frac{1}{3} f (3) - \frac{1}{9} \int_{0}^{3} f (u) d u = \frac{1}{3} .12 - \frac{1}{9} .9 = 3.$

Câu 39:

Cho số phức z thoả mãn . Tính |z|.

A. $|z| = \sqrt{13};$

B. $|z| = \sqrt{5};$

C. |z| = 13;

D. |z| = 5.

Xem đáp án

Đáp án đúng là: A

Đặt z = a + bi $\Rightarrow \bar{z} = a - b i$

Khi đó

$3 (\bar{z} - i) - (2 + 3 i) z = 11 - 24 i$

$\Leftrightarrow 3 \bar{z} - 3 i - (2 + 3 i) z = 11 - 24 i$

$\Leftrightarrow 3 \bar{z} - (2 + 3 i) z = 11 - 21 i$

Û 3(a - bi) - (2 + 3i)(a + bi) = 11 - 21i

Û 3a - 3bi - 2a - 3ai - 2bi -3bi² = 11 - 21i

Û (a + 3b) -(3a + 5b)i = 11 - 21i

$\Rightarrow \{\begin{matrix} a + 3 b = 11 \\ 3 a + 5 b = 21 \end{matrix} \Leftrightarrow \{\begin{matrix} a = 2 \\ b = 3 \end{matrix}$

Khi đó môđun của số phức z là

$|z| = \sqrt{a^{2} + b^{2}} = \sqrt{2^{2} + 3^{2}} = \sqrt{13} .$

Câu 40:

Có bao nhiêu số phức z thỏa mãn $(1 + i) z + \bar{z}$ là số thuần ảo và |z - 2i| = 1?

A. 0;

B. Vô số;

C. 1;

D. 2.

Xem đáp án

Đáp án đúng là: D

Đặt z = a + bi $\Rightarrow \bar{z} = a - b i$

Khi đó

$(1 + i) z + \bar{z} = (1 + i) (a + b i) + (a - b i)$

= a + bi + ai + bi² + a - bi = (2a - b) + ai

Để $(1 + i) z + \bar{z}$ là số thuần ảo nên suy ra

2a - b = 0 Û b = 2a

Khi đó z = a + 2ai

+) |z - 2i| = 1

Û a² + (2a - 2)² = 1

Û 5a² - 8a + 3 = 0

Û 5a² - 5a - 3a + 3 = 0

Û 5a(a - 1) - 3(a - 1) = 0

Û (5a - 3)(a - 1) = 0

$\Rightarrow [\begin{matrix} a = \frac{5}{3} \\ a = 1 \end{matrix}$

Vậy có 2 số phức z thỏa mãn là $z = \frac{5}{3} + \frac{10}{3} i$ và z = 1 + 2i.

Câu 41:

Tính diện tích phần hình phẳng gạch chéo (tam giác cong OAB) trong hình vẽ bên.

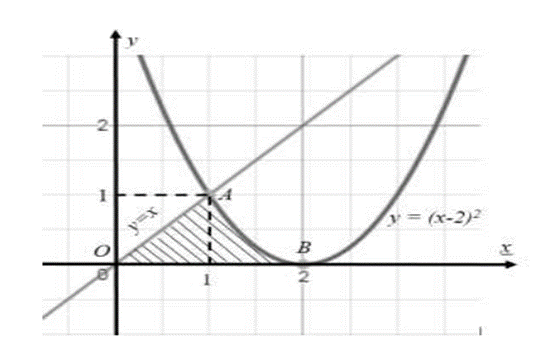
Media VietJack

A. $\frac{8}{15};$

B. $\frac{8 π}{15};$

C. $\frac{5 π}{6};$

D. $\frac{5}{6} .$

Xem đáp án

Đáp án đúng là: D

Gọi S₁ và S₂ lần lượt là diện tích phần gạch chéo của giao giữa đường thẳng y = x với trục hoành trên khoảng (0; 1) và giao của parabol y = (x - 2)² và trục hoành trên khoảng (1; 2)

Ta có:

$S = S_{1} + S_{2} = \int_{0}^{1} x d x + \int_{1}^{2} {(x - 2)}^{2} d x$

$= \int_{0}^{1} x d x + \int_{1}^{2} (x^{2} - 4 x + 4) d x$

$= {\frac{x^{2}}{2}|}_{0}^{1} + {(\frac{x^{3}}{3} - 2 x^{2} + 4 x)|}_{1}^{2}$

$= \frac{1}{2} + (\frac{2^{3}}{3} - {2.2}^{2} + 4.2) - (\frac{1}{3} - 2 + 4) = \frac{5}{6} .$

Câu 42:

Trong không gian Oxyz, cho hai điểm A (1; -1; 2), B(1; 3; 4). Tìm tọa độ điểm M trên trục hoành Ox sao cho biểu thức P = MA² + MB² đạt giá trị nhỏ nhất.

A. M(1; 0; 0);

B. M(2; 0; 0);

C. M(0; 2; 0);

D. M(0; 0; 1).

Xem đáp án

Đáp án đúng là: A

M là điểm nằm trên trục hoành nên suy ra M(m; 0; 0)

Ta có:

P = MA² + MB²

= (m -1)² + 1² + (-2)² + (m - 1)² + (-3)² + (-4)²

= 2(m -1)² + 30 đạt GTNN

Vậy suy ra P_min = 30 Û m - 1 = 0 Û m = 1

Vậy suy ra M(1; 0; 0).

Câu 43:

Biết F (x) là một nguyên hàm của hàm số f (x) = e^3x và F (0) = 0. Giá trị của F (ln3) bằng

A. $\frac{26}{3};$

B. 9;

C. $\frac{8}{3};$

D. 0.

Xem đáp án

Đáp án đúng là: A

Xét $I = \int_{0}^{\ln 3} f (x) d x = \int_{0}^{\ln 3} e^{3 x} d x = \frac{1}{3} \int_{0}^{\ln 3} 3 e^{3 x} d x$

$= {\frac{1}{3} e^{3 x}|}_{0}^{\ln 3} = 9 - \frac{1}{3} = \frac{26}{3}$

Mà $I = \int_{0}^{\ln 3} f (x) d x = {F (x)|}_{0}^{\ln 3} = F (\ln 3) - F (0)$

Nên suy ra $I = F (\ln 3) - F (0) = \frac{26}{3}$

$\Leftrightarrow F (\ln 3) = \frac{26}{3} + F (0) = \frac{26}{3} + 0 = \frac{26}{3} .$

Câu 44:

Kí hiệu (H) là hình phẳng giới hạn bởi đồ thị hàm số y = 2(x - 1)e^x, trục tung và trục hoành. Tính thể tích V của khối tròn xoay thu được khi quay hình (H) xung quanh trục Ox

A. V = (e² - 5)p;

B. V = e² - 5;

C. V = 4 - 2e;

D. V = (4 - 2e)p.

Xem đáp án

Đáp án đúng là: A

Hoành độ giao điểm của đồ thị hàm số y = 2(x - 1)e^x và trục hoành là nghiệm cuat phương trình

2(x - 1)e^x = 0

Û x - 1 = 0 Û x = 1 (do 2e^x > 0 với mọi x)

Thể tích V của khối tròn xoay thu được khi quay hình (H) xung quanh trục Ox là

$V = π \int_{0}^{1} {[2 (x - 1) e^{x}]}^{2} d x = π \int_{0}^{1} [4 (x^{2} - 2 x + 1) e^{2 x}] d x$

Đặt $\{\begin{matrix} u = x^{2} - 2 x + 1 \Rightarrow d u = (2 x - 2) d x \\ d v = 4 e^{2 x} d x \Rightarrow v = 2 e^{2 x} \end{matrix}$

Nên suy ra $V = π \int_{0}^{1} {[2 (x - 1) e^{x}]}^{2} d x$

$= π [{2 {(x - 1)}^{2} e^{2 x}|}_{0}^{1} - \int_{0}^{1} 4 (x - 1) e^{2 x} d x] = π [- 2 - \int_{0}^{1} 4 (x - 1) e^{2 x} d x]$

Đặt $\{\begin{matrix} u = x - 1 \Rightarrow d u = d x \\ d v = 4 e^{2 x} d x \Rightarrow v = 2 e^{2 x} \end{matrix}$

Khi đó $V = π [- 2 - ({2 (x - 1) e^{2 x}|}_{0}^{1} - \int_{0}^{1} 2 e^{2 x} d x)]$

$= π [- 2 - ({2 (x - 1) e^{2 x}|}_{0}^{1} - {e^{2 x}|}_{0}^{1})] = π [- 2 - (2 - e^{2} + 1)]$

= (e² - 5)p.

Câu 45:

Trong không gian Oxyz, cho hai mặt phẳng: (P): 5x - 3y + 2z - 19 = 0, (Q): x - y + z - 3 = 0. Tìm phương trình đường thẳng ∆ là giao tuyến của hai mặt phẳng (P), (Q).

A. $\frac{x - 1}{2} = \frac{y - 3}{2} = \frac{z - 2}{1};$

B. $\frac{x + 5}{1} = \frac{y + 2}{3} = \frac{z}{2};$

C. $\frac{x + 2}{- 1} = \frac{y + 2}{- 3} = \frac{z}{- 2};$

D. $\frac{x - 5}{1} = \frac{y - 2}{3} = \frac{z}{2} .$

Xem đáp án

Đáp án đúng là: D

+) $\vec{n_{P}} = (5; - 3; 2)$ và $\vec{n_{Q}} = (1; - 1; 1)$

Đường thẳng ∆ là giao tuyến của hai mặt phẳng (P), (Q) nên suy ra véc-tơ pháp tuyến của (P) và (Q) đều vuông góc với véc-tơ chỉ phương của ∆

$\vec{u_{Δ}} = [\vec{n_{P}}; \vec{n_{Q}}] = (|\begin{matrix} - 3 & 2 \\ - 1 & 1 \end{matrix}|; |\begin{matrix} 2 & 5 \\ 1 & 1 \end{matrix}|; |\begin{matrix} 5 & - 3 \\ 1 & - 1 \end{matrix}|)$

= (-1; -3; -2) = -(1; 3; 2)

+) Tập hợp giao điểm của (P) và (Q) là nghiệm của phương tình

5x - 3y + 2z - 19 = x - y + z - 3

Û 4x - 2y + z - 16 = 0

Chọn M(5; 2; 0) là một giao điểm bất kỳ

Phương tình đường thẳng D đi qua M và có véc-tơ chỉ phương là (1; 3; 2)

$Δ : \frac{x - 5}{1} = \frac{y - 2}{3} = \frac{z}{2} .$

Câu 46:

Cho hình phẳng giới hạn bởi đồ thị hàm số y = f (x) và trục hoành gồm 2 phần, phần nằm phía trên trục hoành có diện tích $S_{1} = \frac{8}{3}$ và phần nằm phía dưới trục hoành có diện tích $S_{2} = \frac{4}{9}$ . Tính $I = \int_{- 1}^{0} f (3 x + 1) d x .$

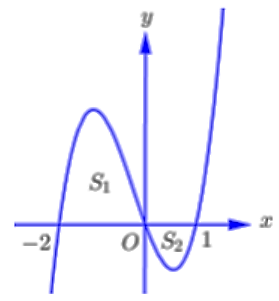
Media VietJack

A. $I = \frac{20}{27};$

B. $I = \frac{3}{4};$

C. $I = \frac{27}{4};$

D. $I = \frac{20}{9} .$

Xem đáp án

Đáp án đúng là: A

Đặt u = 3x + 1 Þ du = 3 dx

Đổi cận:

+) x = -1 Þ u = -2

+) x = 0 Þ u = 1

Khi đó $I = \int_{- 1}^{0} f (3 x + 1) d x$

$= \frac{1}{3} \int_{- 2}^{1} f (u) d u = \frac{1}{3} (\int_{- 2}^{0} f (u) d u + \int_{0}^{1} f (u) d u)$

$= \frac{1}{3} (\int_{- 2}^{0} |f (u)| d u - \int_{0}^{1} |f (u)| d u) = \frac{1}{3} (S_{1} - S_{2})$

$= \frac{1}{3} (\frac{8}{3} - \frac{4}{9}) = \frac{20}{27} .$

Câu 47:

Trong không gian Oxyz, cho mặt phẳng (P) : x - 2y + 2z - 5 = 0 và hai điểm A(-3; 0; 1), B(1; -1; 3). Tìm phương trình của đường thẳng ∆ đi qua A và song song với (P) sao cho khoảng cách từ B đến đường thẳng ∆ là nhỏ nhất.

A. $\frac{x - 2}{26} = \frac{y + 1}{11} = \frac{z - 3}{- 2};$

B. $\frac{x + 2}{26} = \frac{y - 1}{11} = \frac{z + 3}{- 2};$

C. $\frac{x - 3}{26} = \frac{y}{11} = \frac{z + 1}{- 2};$

D. $\frac{x + 3}{26} = \frac{y}{11} = \frac{z - 1}{- 2} .$

Xem đáp án

Đáp án đúng là: D

+) $\vec{n_{P}} = (1; - 2; 2)$

+) $\vec{A B} = (4; - 1; 2)$

Viết phương trình mặt phẳng (Q) qua A và song song với mặt phẳng (P) là:

(Q): x - 2y + 2z + m = 0

Mặt phẳng (Q) qua A Þ -3 + 2 + m = 0 Û m = 1

Vậy (Q): x - 2y + 2z + 1 = 0

Lấy H là hình chiếu của B lên (Q)

Đường thẳng BH qua B và có véc-tơ chỉ phương là $\vec{n_{Q}} = (1; - 2; 2)$

$B H : \{\begin{matrix} x = 1 + t \\ y = - 1 - 2 t \\ z = 3 + 2 t \end{matrix}$

H là giao của BH và (Q) nên ta có

(1 + t) - 2(-1 - 2t) + 2(3 + 2t) + 1 = 0

Û 9t + 10 = 0 $\Leftrightarrow t = \frac{- 10}{9}$

Vậy $H (\frac{- 1}{9}; \frac{11}{9}; \frac{7}{9})$

$\Rightarrow \vec{A H} = (\frac{26}{9}; \frac{11}{9}; \frac{- 2}{9}) = \frac{1}{9} (26; 11; - 2)$

Vậy phương trình cần tìm là phương trình AH đi qua A(-3; 0; 1) và có véc-tơ chỉ phương là (26; 11; -2)

$A H : \frac{x + 3}{26} = \frac{y}{11} = \frac{z - 1}{- 2} .$

Câu 48:

Cho hai số phức z₁, z₂, thỏa mãn |z₁ + 6| = 5, |z₂ + 2 - 3i| = |z₂ - 2 - 6i|. Giá trị nhỏ nhất của |z₁ - z₂| bằng

A. $\frac{3 \sqrt{2}}{2};$

B. $\frac{7 \sqrt{2}}{2};$

C. $\frac{5}{2};$

D. $\frac{3}{2} .$

Xem đáp án

Đáp án đúng là: C

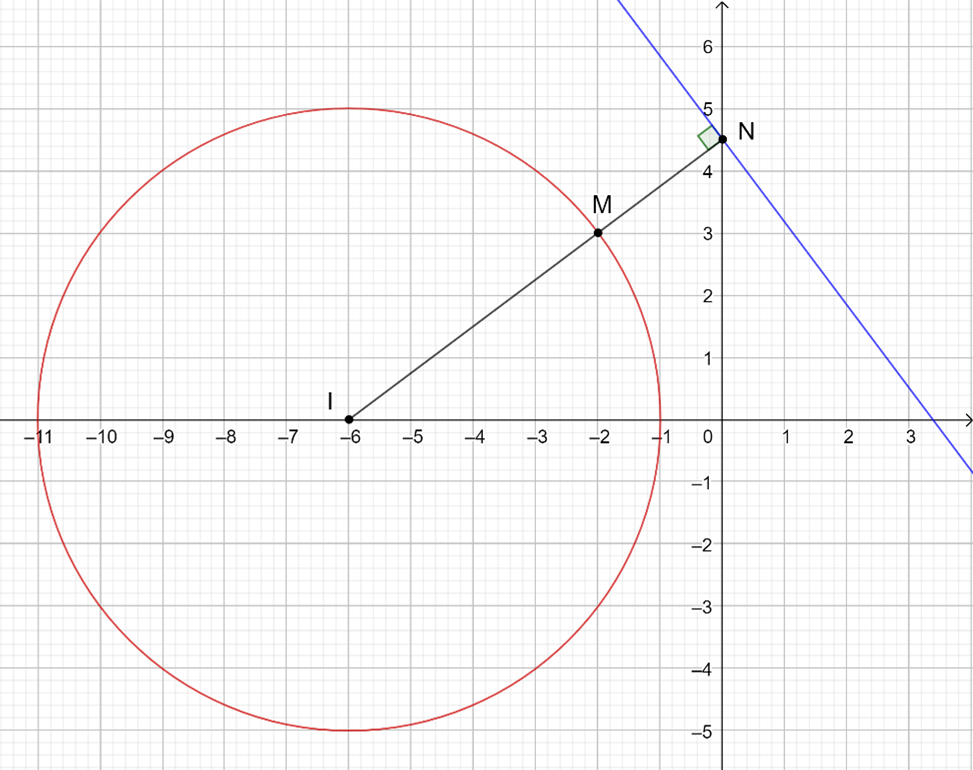
+) |z₁ + 6| = 5

Û (x₁ + 6)² + y₁² = 25

M(x₁; y₁) là điểm biểu diễn của số phức z₁ và thuộc đường tròn tâm I(-6; 0) có bán kính R = 5

+) |z₂ + 2 - 3i| = |z₂ - 2 - 6i|

Û (x₂ + 2)² + (y₂ - 3)² = (x₂ - 2)² + (y₂ - 6)²

Û x₂² + 4x₂ + 4 + y₂² - 6y₂ + 9 = x₂² - 4x₂ + 4 + y₂² - 12y₂ + 36

Û 8x₂ + 6y₂ - 27 = 0

N(x₂; y₂) là điểm biểu diễn của số phức z₂ và thuộc đường thẳng 8x + 6y - 27 = 0

Ta có |z₁ - z₂| bằng MN và để |z₁ - z₂| đạt GTNN thì MN nhỏ nhất

Khi đó đường thẳng MN đi qua I, vuông góc với đường thẳng trên và M gần N nhất

Theo hình vẽ

MN_min = IN - IM

Với $I N = d_{I / d} = \frac{|8. (- 6) - 27|}{\sqrt{8^{2} + 6^{2}}} = \frac{15}{2}$ và IM = R = 5

Nên suy ra $M N_{\min} = \frac{15}{2} - 5 = \frac{5}{2} .$

Câu 49:

Trong không gian Oxyz, cho mặt cầu (S) có tâm thuộc mặt phẳng (P): x + 2y + z - 7 = 0 và đi qua hai điểm A(1; 2; 1), B(2; 5; 3). Bán kính nhỏ nhất của mặt cầu (S) bằng

A. $\frac{\sqrt{345}}{3};$

B. $\frac{\sqrt{470}}{3};$

C. $\frac{\sqrt{546}}{3};$

D. $\frac{\sqrt{763}}{3} .$

Xem đáp án

Đáp án đúng là: C

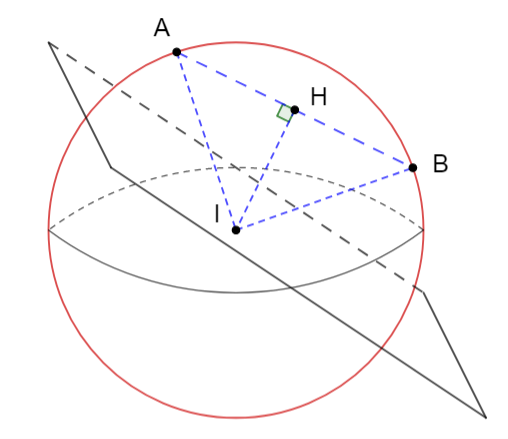
Gọi tâm I(x; y; z)

Mặt cầu (S) đi qua hai điểm A(1; 2; 1), B(2; 5; 3) nên ta có:

IA = IB = R

Ta có:

+) $R = I A = \sqrt{A H^{2} + I H^{2}}$

+) $\vec{A B} = (1; 3; 2)$

+) $H (\frac{3}{2}; \frac{7}{2}; 2)$ là trung điểm của đoạn thẳng AB

+) IA = IB

$\Leftrightarrow \sqrt{{(x - 1)}^{2} + {(y - 2)}^{2} + {(z - 1)}^{2}} = \sqrt{{(x - 2)}^{2} + {(y - 5)}^{2} + {(z - 3)}^{2}}$

$\Leftrightarrow \sqrt{x^{2} + y^{2} + z^{2} - 2 x - 4 y - 2 z + 6} = \sqrt{x^{2} + y^{2} + z^{2} - 4 x - 10 y - 6 z + 38}$

Þ x² + y² + z² - 2x - 4y - 2z + 6 = x² + y² + z² - 4x - 10y - 6z + 38

Û 2x + 6y + 4z = 32

Û x + 3y + 2z = 16

Do I thuộc các mặt phẳng (P) và IA = IB = R nên ta có hệ phương trình

$\{\begin{matrix} x + 2 y + z = 7 \\ x + 3 y + 2 z = 16 \end{matrix} \Leftrightarrow \{\begin{matrix} y + z = 9 \\ x + 2 y + z = 7 \end{matrix}$

$\Leftrightarrow \{\begin{matrix} y = 9 - z \\ x + 2 y + z = 7 \end{matrix} \Leftrightarrow \{\begin{matrix} y = 9 - z \\ x = z - 11 \end{matrix}$

Vậy suy ra I(z - 11; 9 - z; z)

Khi đó $I A = \sqrt{{(z - 12)}^{2} + {(7 - z)}^{2} + {(z - 1)}^{2}}$

$= \sqrt{(z^{2} - 24 z + 144) + (z^{2} - 14 z + 49) + (z^{2} - 2 z + 1)}$

$= \sqrt{3 z^{2} - 40 z + 194} = \sqrt{(3 z^{2} - 2 z \sqrt{3} . \frac{20}{\sqrt{3}} + \frac{400}{3}) + \frac{182}{3}}$

$= \sqrt{{(z \sqrt{3} - \frac{20}{\sqrt{3}})}^{2} + \frac{182}{3}} \geq \sqrt{\frac{182}{3}} = \frac{\sqrt{546}}{3}$

Vậy R đạt GTNN là $\frac{\sqrt{546}}{3}$ khi và chỉ khi

$\Leftrightarrow z \sqrt{3} - \frac{20}{\sqrt{3}} = 0 \Leftrightarrow z = \frac{20}{3}$

Khi đó $I (\frac{- 13}{3}; \frac{7}{3}; \frac{20}{3}) .$

Câu 50:

Cho f (x) là hàm số liên tục trên ℝ thỏa mãn f (x) + f '(x) = x + 1 với mọi x và f (0) = 3. Tính e.f (1).

A. e + 3;

B. e - 3;

C. e + 1;

D. e - 1.

Xem đáp án

Đáp án đúng là: A

f (x) + f '(x) = x + 1 (1)

Với e^x > 0 với moi x nên nhân 2 vế của (1) với e^x ta được

e^x.f (x) + e^x.f '(x) = (x + 1).e^x

Lấy nguyên hàm hai vế ta có:

$\int [e^{x} . f (x) + e^{x} . f' (x)] d x = \int (x + 1) e^{x} d x$

+) Xét $V T = \int [e^{x} . f (x) + e^{x} . f' (x)] d x$

$= \int [(e^{x})' . f (x) + e^{x} . f' (x)] d x = e^{x} . f (x) + C$

+) $V P = \int (x + 1) e^{x} d x$

Đặt $\{\begin{matrix} u = x + 1 \Rightarrow d u = d x \\ d v = e^{x} d x \Rightarrow v = e^{x} x \end{matrix}$

Suy ra $V P = \int (x + 1) e^{x} d x = (x + 1) e^{x} - \int e^{x} d x$

= x.e^x + C

Khi đó phương trình (2) trở thành

(2) Û e^x.f (x) = x.e^x + C

Thay x = 0 vào ta được

e⁰.f (0) = 0.e⁰ + C Û 3 = C

Vậy suy ra e^x.f (x) = x.e^x + 3

Khi đó e.f (1) = 1.e¹ + 3 = e + 3.

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đề kiểm tra Học kì 2 Toán 12 có đáp án (Mới nhất)

Đề kiểm tra Học kì 2 Toán 12 có đáp án (Mới nhất) - Đề 13

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương