Bài tập chuyên đề Toán 7 Dạng 6: Đại lượng tỷ lệ nghịch có đáp án - Đề 1
-
307 lượt thi
-
31 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Các giá trị tương ứng của x và y được cho trong hai bảng:
Bảng I
|
x |
3 |
-4,5 |
5 |
0,75 |
|
22,5 |
-7,5 |
|
|
y |
-15 |
10 |
-9 |
-60 |
-2,5 |
|
|
-8 |
Bảng II
|
x |
3 |
-0,5 |
-6 |
0,95 |
|
0,35 |
|
|
|
y |
15 |
-2,5 |
-30 |
4,75 |
-7,5 |
|
|
1975 |
a) Xác định xem hai đại lượng y và x trong bảng nào tỉ lệ thuận? tỉ lệ nghịch? Tìm các hệ số tỉ lệ (biết các giá trị tương ứng còn lại cùng có quan hệ tỉ lệ như các giá trị đã cho trong bảng).
b) Điền tiếp các giá trị vào ô trống.
Tại bảng I: Ta có 3.(-15) = -4,5.10 = 5. (-9) = -0,75.60 = -45
Nên y tỉ lệ nghịch với x. Hệ số tỉ lệ -45. Công thức x.y = -45.
Bảng I
|
x |
3 |
-4,5 |
5 |
0,75 |
18 |
22,5 |
-7,5 |
5,625 |
|
y |
-15 |
10 |
-9 |
-60 |
-2,5 |
-2 |
6 |
-8 |
Tại bảng II:
Nên y tỉ lệ thuận với x. Hệ số tỉ lệ 5. Công thức y=5x
Bảng II
|
x |
3 |
-0,5 |
-6 |
0,95 |
-1,5 |
0,35 |
|
395 |
|
y |
15 |
-2,5 |
-30 |
4,75 |
-7,5 |
1,75 |
-2 |
1975 |
Câu 2:
Cho hai đại lượng tỉ lệ nghịch x và y; x1 và x2 là hai giá trị của x và y1 và y2 là hai giá trị tương ứng của y.
Biết y1 =3,5; y2 =2,5 và 8x2 - 5x1 = 31
Tính x1;x2 và hệ số tỉ lệ a của hai đại lượng tỉ lệ nghịch này.
Theo tính chất của đại lượng tỉ lệ nghịch, và áp dụng tính chất dãy tỉ số bằng nhau ta có:
Do dó x1= y2 : 0,5 = 5
Và x2 = y1 : 0,5 = 7
Hệ số tỉ lệ của hai đại lượng là: a = x1 . y1 = 5.3,5=17,5
Câu 3:
Năm máy cày cùng loại, mỗi máy làm 8 giờ một ngày thì trong 12 ngày cày xong một cánh đồng.
a) Nếu có 10 máy cày cùng loại trên, mỗi máy làm 8 giờ một ngày thì trong mấy ngày cày xong cánh đồng trên.
Gọi số ngày cần tìm là z ngày ( z > 0 ). Cùng một công việc và số giờ làm việc một ngày của mỗi máy, số máy cày và số ngày là hai đại lượng tỉ lệ nghịch.
Ta có: (ngày).
* Có thể lý luận cách khác :
Một ngày 5 máy cày với tổng số giờ là 5.8 = 40 (giờ)
Một ngày 10 máy cày với tổng số giờ là 10.8 = 80 (giờ)
Cùng một công việc tổng số giờ làm 1 ngày và số ngày hoàn thành công việc là hai đại lượng tỉ lệ nghịch.
Do đó (ngày).
Câu 4:
b) Cần bao nhiêu máy cày, mỗi máy làm 6 giờ mỗi ngày để 5 ngày cày xong cánh đồng ấy ?
Gọi số máy cày cần tìm là t (cái).
Số giờ năm máy cày xong cánh đồng là 8.12 = 96 (giờ).
Số giờ x máy cày xong cánh đồng là 6.5 = 30 (giờ).
Trên cùng một cánh đồng số máy cày và số giờ làm là hai đại lượng tỉ lệ nghịch. Do đó ta có :
Vậy số máy cày cần tìm là 16 cái.
Câu 5:
Ba cạnh a,b,c của có 4a+6b-5c = 220cm. Ba đường cao tương ứng là ha;hb;hc tỉ lệ thuận với 3;4;5. Tính chu vi của tam giác.
Gọi diện tích của là S. Ta biết rằng 2S = aha = bhb = chc nên trong một tam giác cạnh và đường cao tương ứng tỉ lệ nghịch với nhau.
Biết ha:hb:hc=3 : 4 :5 nên a:b:c= = 20:15:12
Tức là
Vậy chu vi tam giác là 20.2+15.2+12.2=94(cm).
Câu 6:
Một ô tô dự định chạy từ A đến B trong một thời gian nhất định. Nếu xe chạy với vận tốc 40km/h thì đến B muộn hơn so với dự định là 30 phút. Nếu xe chạy với vận tốc 60km/h thì đến B sớm hơn so với dự định là 45 phút. Tính thời gian dự định đi và quãng đường AB.
Ta có 45 phút = 0,75 giờ; 30 phút = 0,5 giờ.
Gọi thời gian dự định là t (giờ); (t>0) ; Thời gian xe chạy quãng đường AB với vận tốc 40km/h là t1 = (t + 0,5) (giờ). Thời gian xe chạy quãng đường AB với vận tốc 60km/h là t2 = ( t - 0,75). Cùng một quãng đường thì vận tốc và thời gian đi tương ứng tỉ lệ nghịch với nhau. Do đó theo tính chất của tương quan tỉ lệ nghịch, ta có:
(giờ).
Thời gian dự định là: 3,75 – 0,5 = 3,25 (giờ) = 3 giờ 15 phút.
Quãng đường AB dài là: 3,75.40 = 150(km).
Câu 7:
Bốn người mua cùng một số mét vuông vải để may quần áo lần luợt theo bốn loại khổ rộng 1,5m; 1,2m; 1,0m; 0,8m. Tổng số vải bốn người đã mua là 22,5m. Tính số mét vải và diện tích vải mỗi người đã mua.
Cùng một diện tích, số m vải tỉ lệ nghịch với khổ rộng của nó. Gọi số mét vải mỗi người mua lần lượt là x,y,z,t (x,y,z,t > 0 ) ta có:
1,5x=1,2=z=0,8t hay 15x=12y=10z=8t
Vậy: x=8.0,5=4(m) ; y= 10.0,5=5(m)
z=12.0,5=6(m) ; t = 15.0,5=7,5 (m).
Diện tích vải mỗi người mua là: 4.1,5=6m2.
Câu 8:
Tại một bến xe có 610 xe ô tô chở khách gồm 4 loại: Xe chở 50 khách; xe chở 45 khách; xe chở 30 khách và xe chở 25 khách. Biết rằng số xe chở khách 50 khách bằng xe chở 45 khách, bằng số xe chở 30 khách và bằng xe chở 25 khách. Hỏi bến xe có bao nhiêu xe mỗi loại
Gọi số xe các loại chở 50 khách; chở 45 khách; chở 30 khách và chở 25 khách lần lượt là x;y;z;t (x;y;z;t >0) ta có:
x +y+z+t = 610 và
.
Hay .
Suy ra x=180; y=160; z=150;t=120
Câu 9:
Một bộ máy truyền chuyển động có ba bánh xe răng được khớp vào nhau: bánh xe thứ nhất khớp với bánh xe thứ hai; bánh xe thứ hai khớp với bánh xe thứ ba.
a) Nếu bánh xe thứ nhất có 90 răng và quay 36 vòng/phút thì bánh xe thứ hai có 72 răng sẽ quay được bao nhiêu vòng/phút?
Ta có hai bánh xe khớp vào nhau trong quá trình chuyển động nên số răng và số vòng quay của bánh xe là hai đại lượng tỉ lệ nghịch. Vì thế:
Gọi số vòng quay của bánh xe thứ hai là x (x>0) thì
Suy ra x=90.36:72=45 (vòng).
Câu 10:
b) Muốn bánh xe thứ ba quay 180 vòng/phút thì bánh xe thứ ba cần thiết kế có bao nhiêu răng?
Gọi số răng của bánh xe thứ ba là y thì
Suy ra y = 45.72 :180 = 18 (răng).
Câu 11:
Để làm xong một công việc 48 công nhân cần làm trong 30 ngày (năng suất lao động mỗi người như nhau). Nếu số công nhân tăng thêm 25% và năng suất lao động mỗi người đều tăng thêm 20% thì cần làm bao lâu để xong công việc đó?
Số công nhân sau khi tăng có 48 + 48.25% = 48 + 12 = 60 (người)
Giữ nguyên năng suất lao động cũ. Cùng một công việc, cùng năng suất lao động thì số công nhân tỉ lệ nghịch với số ngày làm. Gọi số ngày làm của số 60 công nhân theo năng suất cũ là x ta có:
(ngày).
Năng suất lao động mới là: 100% + 20% = 120%.
Cùng một công việc, cùng số công nhân thì số ngày làm tỉ lệ nghịch với năng suất lao động. Gọi số ngày 60 công nhân làm theo năng suất mới là y thì ta có (ngày).
Câu 12:
Cho biết hai đại lượng x và y tỷ lệ nghịch với nhau. Tìm công thức liên hệ giữa y và x. Điền số thích hợp vào ô trống trong bảng sau;
|
x |
-40 |
|
-8 |
-0,5 |
|
16 |
|
6,4 |
|
y |
|
4 |
|
-160 |
20 |
|
-3,2 |
|
|
x |
-40 |
20 |
-8 |
-0,5 |
4 |
16 |
-25 |
6,4 |
|
y |
-2 |
4 |
-10 |
-160 |
20 |
5 |
-3,2 |
12,5 |
Câu 13:
Cho hai đại lượng tỉ lệ nghịch z và t; z1 và z2 là hai giá trị của z, t1 và t2 là hai giá trị tương ứng của t. Biết z2=8; 2z1-3z2=10 và t1=4. Tính z1;t2.
Và từ
Câu 14:
Tìm hai số dương biết tổng, hiệu, tích của chúng tỉ lệ nghịch với 50; 125 và 25.
Gọi hai số phải tìm là x;y ( x;y >0). Tổng, hiệu, tích của chúng tỉ lệ nghịch với 50; 125 và 25 nghĩa là tỉ lệ thuận với
(x+y):(x-y):xy = Hay
Suy ra 7y=20
Câu 15:
Một số dương M được chia làm bốn phần đều là các số dương tỷ lệ nghịch với 2:3:4:5. Biết hiệu giữa tổng các bình phương của phần thứ nhất và phần thứ hai với tổng các bình phương của phần thứ ba và thứ tư là 3724. Tìm số M.
Gọi bốn phần của M là x;y;z;t (x;y;z;t >0)
Ta có: x:y:z:t=
Hay =k
Do các phần đều dương nên k=2
và M=154.
Câu 16:
a:b:c =
Hay
Vậy k=-2
Câu 17:
Cho ba số a;b;c tỷ lệ nghịch với
Tính giá trị biểu thức A=.
Ta có
a=2017k ; b=2018k ; c=2019k
Do đó A=
Câu 18:
Một tam giác ABC có chu vi 105cm. Các đường cao trong tam giác ABC ứng với cạnh là BC = a là ha=28cm ứng với cạnh AB = c là hc=32cm. Biết với AC=b.
Tính độ dài mỗi cạnh của tam giác nói trên.
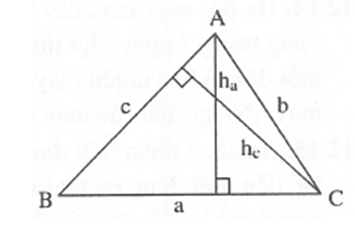
Do đó
và a + c = 105 -30 = 75cm
Cùng một diện tích, thì cạnh đáy tỉ lệ nghịch với chiều cao tương ứng
Do đó ta có:
Vậy BC = a = 32. ; AB=c=28.
Câu 19:
Một ô tô và một xe máy cùng khởi hành một lúc từ A đến B. Vận tốc của ô tô là 60km/h. Vận tốc của xe máy là 45km/h. Ô tô đến B trước xe máy là 30 phút. Tính quãng đường AB.
Ta có 30 phút = 0,5 giờ. Cùng một quãng đường AB thì vận tốc và thời gian đi tương ứng tỉ lệ nghịch với nhau. Gọi t1 là thời gian xe ô tô đi hết quãng đường AB, t2 là thời gian xe máy đi hết quãng đường AB,
Theo tính chất của hai đại lượng tỉ lệ nghịch ta có:
Ta có: (giờ).
Quãng đường AB dài là: 2.45 = 90(km).
Câu 20:
Một ô tô chạy trên đoạn đường AB gồm bốn chặng đường dài bằng nhau với tốc độ lần lượt là 50km/h; 40km/h; 60km/h và 30km/h. Biết tổng thời gian đi cả bốn chặng là 19 giờ. Tính quãng đường AB.
Với quãng đường như nhau thì vận tốc tỉ lệ nghịch với thời gian. Gọi thời gian đi trên bốn đoạn đường lần lượt là x;y;z;t (giờ) (x;y;z;t >0 ).
Ta có: 50x=40y=60z=30t=s
x= 12.= 4 (giờ). Mỗi chặng dài 4.50=200 km.
Quãng đường AB dài 4.200=800km.
Câu 21:
Hai ô tô cùng khởi hành từ A đến B. Biết tỷ số vận tốc ô tô thứ hai và ô tô thứ nhất là 3: 5. Ô tô thứ nhất đến B sớm hơn 1 giờ 30 phút so với ô tô thứ hai.Tính thời gian mỗi xe đi từ A đến B
Gọi v1 là vận tốc ô tô thứ nhất, v2 là vận tốc ô tô thứ hai (v1;v2 > 0) ta có . Cùng quãng đường thì vận tốc và thời gian là hai đại lượng tỉ lệ nghịch. Gọi t1 là thời gian ô tô thứ nhất đi hết quãng đường AB; t2 là thời gian ô tô thứ hai đi hết quãng đường AB (t1;t2 >0) ta có:
Vậy: t2 = (giờ) = 3 giờ 45 phút;
t1=3. (giờ) = 2 giờ 15 phút.
Câu 22:
Trên đoạn đường AB lúc 7 giờ sáng một xe tải đi từ A với vận tốc 45km/h đến B lúc 11 giờ. Cùng lúc 7 giờ một ô tô khởi hành từ A đi đến B và một xe máy khởi hành từ B đi đến A. Ô tô và xe máy gặp nhau tại C trên AB. Tính độ dài đoạn AC. Biết rằng thời gian xe ô tô đi hết quãng đường AB và thời gian xe máy đi hết đoạn đường BA tỉ lệ thuận với 3 và 5.
Quãng đường AB dài: 45.( 11 - 7 ) = 180km. Gọi s1 = AC; và v1 km/h là vận tốc của xe ô tô; v2 km/h là vận tốc của xe máy (s1;s2;.s3;s4)
Cùng một quãng đường thì thời gian và vận tốc là hai đại lượng tỉ lệ nghịch. Do thời gian xe ô tô đi hết quãng đường AB và thời gian xe máy đi hết đoạn đường BA tỉ lệ thuận với 3 và 5 nên ![]() . Từ lúc khởi hành đến lúc gặp nhau hai xe đi trong cùng một thời gian nên quãng đường đi được và vận tốc là hai đại lượng tỉ lệ thuận.
. Từ lúc khởi hành đến lúc gặp nhau hai xe đi trong cùng một thời gian nên quãng đường đi được và vận tốc là hai đại lượng tỉ lệ thuận.
Do đó . Từ
.
Câu 23:
Một động tử (vật chuyển động) chạy trên 3 cạnh của một tam giác đều (có ba cạnh bằng nhau) với vận tốc lần lượt là 6m/s; 5m/s; 4m/s. Tính chu vi tam giác biết tổng số thời gian động tử chuyển động trên ba cạnh là 111 giây.
Ba cạnh tam giác bằng nhau. Cùng đoạn đường vận tốc và thời gian là hai đại lượng tỉ lệ nghịch.Gọi thời gian động tử trên 3 cạnh lần lượt là t1;t2;t3 (giây); (t1;t2;t3 > 0).
Ta có: t1 : t2 :t3 = =10:12:15
Hay .
Ta có t1 =30 giây và cạnh tam giác dài là 30.6=180 m.
Chu vi tam giác là: 180.3 = 540 m.
Câu 24:
Để làm xong một công việc 42 công nhân dự định làm trong 14 ngày (năng suất lao động mỗi người như nhau). Khi tiến hành công việc số công nhân được điều đi làm việc khác. Số công nhân còn lại năng suất lao động mỗi người đều tăng thêm 50%. Hỏi đội công nhân có hoàn thành đúng thời gian dự định?
Số người còn lại làm công việc là 42 - 42 :3 = 28 (công nhân). Năng suất lao động mới là: 100% + 50% = 150%
Giữ nguyên năng suất lao động cũ. Cùng một công việc, cùng năng suất lao động thì số công nhân tỉ lệ nghịch với số ngày làm. Gọi số ngày làm của số 28 công nhân theo năng suất cũ là x (x > 0)ta có:
(ngày)
Cùng một công việc, cùng số công nhân thì số ngày làm tỉ lệ nghịch với năng suất lao động. Gọi số ngày 28 công nhân làm theo năng suất mới là y ( y>0)
Thì ta có: (ngày).
Câu 25:
Ba đội công nhân đào ba con mương như nhau với năng suất lao động mỗi người như nhau. Đội I hoàn thành trong 5 ngày; đội II hoàn thành trong 6 ngày; đội III hoàn thành trong 8 ngày. Số người của đội I nhiều hơn số người của đội III là 18 người. Hỏi mỗi đội có bao nhiêu người?
Cùng khối lượng công việc (ba con mương như nhau), năng suất lao động mỗi người như nhau thì số người làm và thời gian hoàn thành công việc là hai đại lượng tỉ lệ nghịch. Gọi x;y;z là số công nhân của mỗi đội .
Ta có: x : y :z =
Vậy x=48 (người); y = 40 (người); z = 30 (người).
Câu 26:
Ba đội máy cày, cày ba cánh đồng cùng diện tích. Đội thứ nhất cày xong trong 3 ngày, đội thứ hai trong 5 ngày, đội thứ ba trong 6 ngày; Hỏi mỗi đội có bao nhiêu máy, biết rằng đội thứ hai có nhiều hơn đội thứ ba 1 máy. (Năng suất các máy như nhau).
Gọi số máy của ba đội theo thứ tự là x;y;z. Vì cùng diện tích cày, số máy và số ngày cày xong cánh đồng là hai đại lượng tỉ lệ nghịch nên x:y:z =
(máy); y = 6 (máy); z = 5 (máy).
Câu 27:
Ba công nhân tiện được tất cả 860 dụng cụ trong cùng một thời gian. Để tiện một dụng cụ người thứ nhất cần 5 phút, người thứ hai cần 6 phút, người thứ ba cần 9 phút. Tính số dụng cụ mỗi người tiện được?
Gọi số dụng cụ của ba công nhân tiện được theo thứ tự là x;y;z.
Vì cùng thời gian số dụng cụ tiện được của mỗi người và thời gian tiện xong một dụng cụ là hai đại lượng tỉ lệ nghịch nên
x : y : z =
z=200(dụng cụ); (dụng cụ); y = 300 (dụng cụ).
Câu 28:
Ba đội máy san đất làm ba khối lượng công việc như nhau. Đội thứ nhất hoàn thành công việc trong 4 ngày, đội thứ hai trong 6 ngày. Hỏi đội thứ ba hoàn thành trong mấy ngày, biết rằng tổng số máy của đội một và đội hai gấp 10 lần số máy đội ba (giả thiết năng suất của các máy như nhau)?
Gọi số máy của ba đội theo thứ tự là x;y;z và t là số ngày đội thứ ba cần dùng để hoàn thành công việc .
Vì cùng công việc số máy và số ngày là hai đại lượng tỉ lệ nghịch nên
x : y : z =
(ngày).
Câu 30:
Gọi x;y;z là ba số cần tìm thì x + y + z = 420
Ta có
Câu 31:
Tìm x;y;z biết rằng x và y tỉ lệ nghịch với 3 và 2; y và z tỉ lệ nghịch với 4 và 5 và 3x2-y2 +z2=1971.
Ta có: 3x=2y và 4y=5z và
; y=15k ; z=12k. Thay vào 3x2-y2+z2 =1971
