Trắc nghiệm bài tập theo tuần Toán 7-Tuần 19 có đáp án
-
317 lượt thi
-
12 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Số lượng học sinh giỏi Toán trong từng lớp của một trường THCS được ghi lại trong bảng sau:
|
14 |
16 |
12 |
15 |
11 |
12 |
11 |
13 |
|
14 |
15 |
13 |
15 |
12 |
12 |
11 |
12 |
|
13 |
14 |
13 |
17 |
12 |
12 |
14 |
14 |
Dấu hiệu cần tìm hiểu là số lượng học sinh giỏi Toán trong từng lớp của một trường THCS. Dấu hiệu này có tất cả 24 giá trị.
Câu 2:
Số lượng học sinh giỏi Toán trong từng lớp của một trường THCS được ghi lại trong bảng sau:
|
14 |
16 |
12 |
15 |
11 |
12 |
11 |
13 |
|
14 |
15 |
13 |
15 |
12 |
12 |
11 |
12 |
|
13 |
14 |
13 |
17 |
12 |
12 |
14 |
14 |
Câu 3:
Số lượng học sinh giỏi Toán trong từng lớp của một trường THCS được ghi lại trong bảng sau:
|
14 |
16 |
12 |
15 |
11 |
12 |
11 |
13 |
|
14 |
15 |
13 |
15 |
12 |
12 |
11 |
12 |
|
13 |
14 |
13 |
17 |
12 |
12 |
14 |
14 |
Viết các giá trị khác nhau và tần số của chúng.
Các giá trị khác nhau và tần số tương ứng của nó là:
|
Giá trị |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
|
Tần số |
3 |
7 |
4 |
5 |
3 |
1 |
1 |
Câu 4:
Em hãy điều tra xem mỗi bạn trong tổ của mình sinh vào tháng mấy? Lập bảng số liệu thống kê ban đầu và cho biết:
Dấu hiệu mà em quan tâm là gì và dấu hiệu đó có tất cả bao nhiêu giá trị?
Câu 5:
Em hãy điều tra xem mỗi bạn trong tổ của mình sinh vào tháng mấy? Lập bảng số liệu thống kê ban đầu và cho biết:
Có bao nhiêu giá trị khác nhau trong dãy giá trị của dấu hiệu đó
Dấu hiệu này có …….. giá trị khác nhau
Câu 6:
Cho tam giác vuông tại A. Gọi M là trung điểm của cạnh BC. Trên tia đối của tia MA lấy điểm D sao cho
Chứng minh:
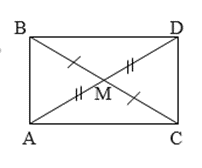
Xét và có: (vì M là trung điểm của BC);
(đđ) ; (gt)
Nên (c.g.c)
Câu 7:
Chứng minh: AB//CD và
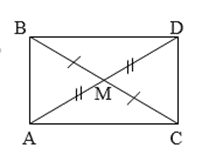
(câu a) nên
Mà hai góc này ở vị trí so le trong nên
Mặt khác (do vuông tại A) nên
và có: (do );
(= 1v) ; cạnh AC chung nên (c.g.c).
Câu 8:
Chứng minh: Tam giác BDC là tam giác vuông.
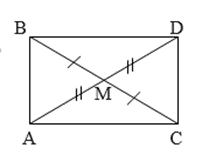
và có: (câu b) ;
BC là cạnh chung nên (c.g.c).
Suy ra .
Vậy tam giác là tam giác vuông.
Câu 9:
Cho tam giác có cạnh Gọi H là trung điểm của BC.
Chứng minh rằng
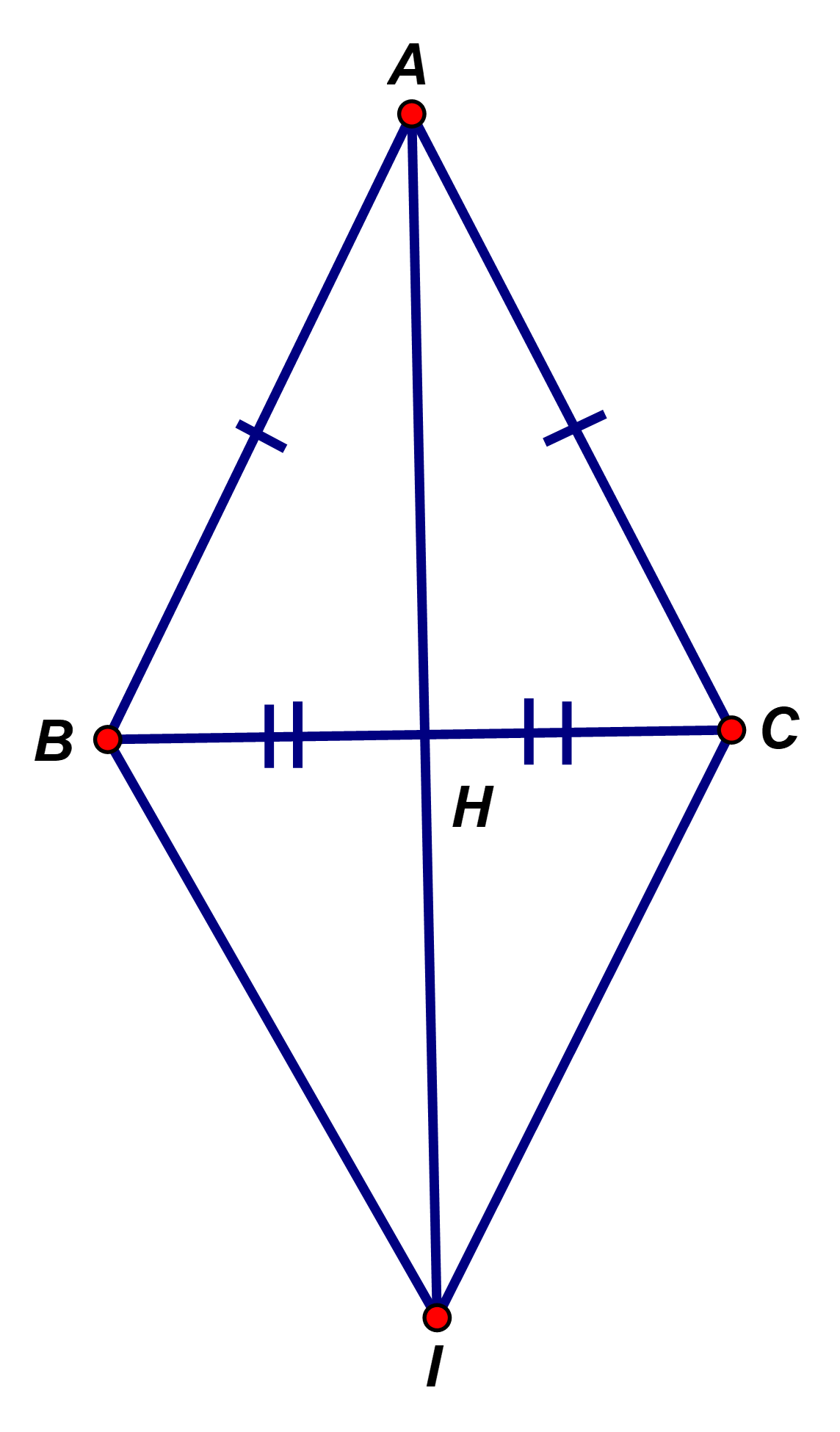
và có:
(gt)
AH cạnh chung
(H là trung điểm BC)
Suy ra: (c-c-c)Câu 10:
Chứng minh rằng AH là đường trung trực của BC
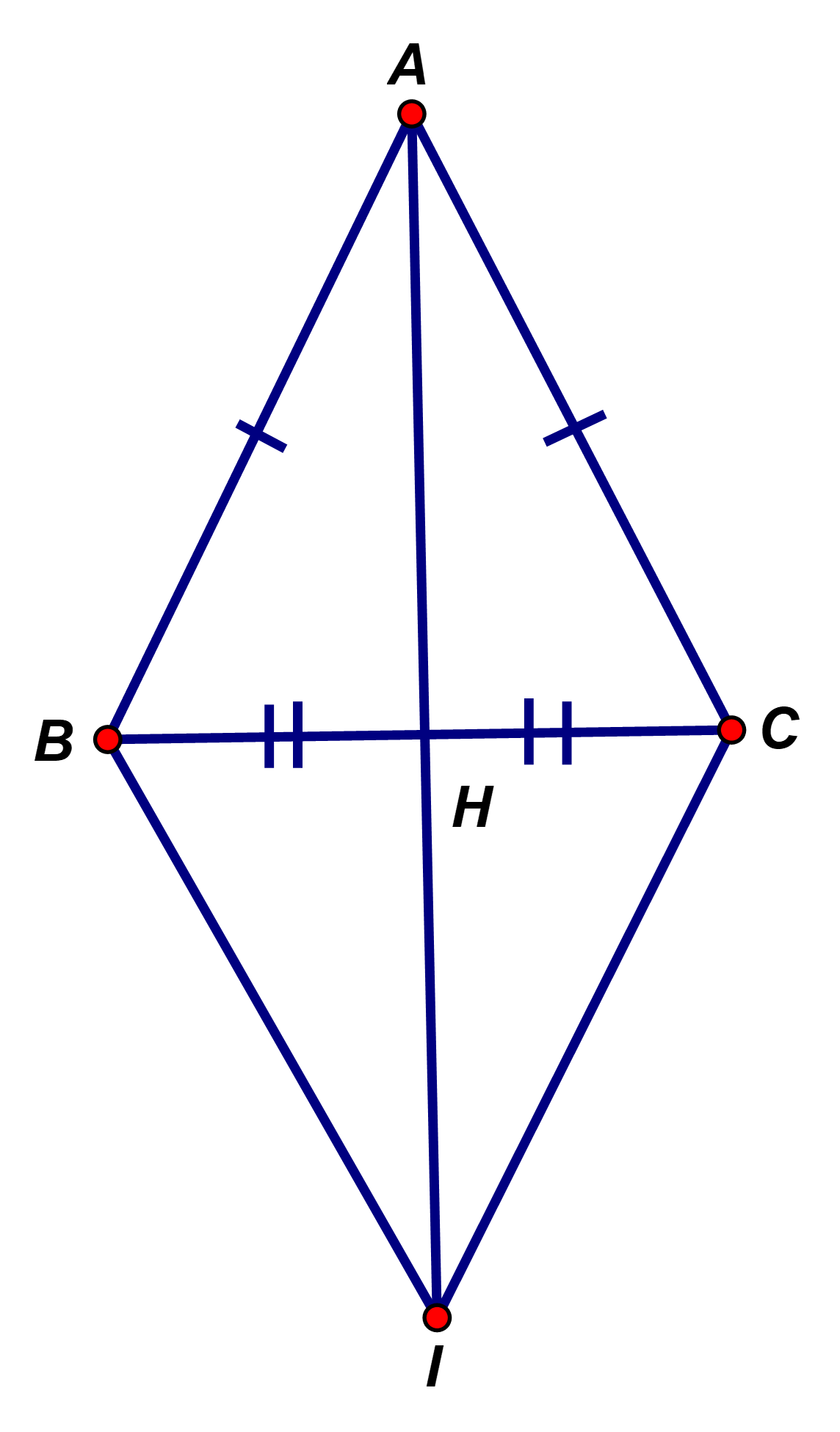
Ta có: ( 2 góc kề bù)
Mà ( do )
Nên :
Mà H là trung điểm của BC (gt)
Nên AH là đường trung trực của BC
Câu 11:
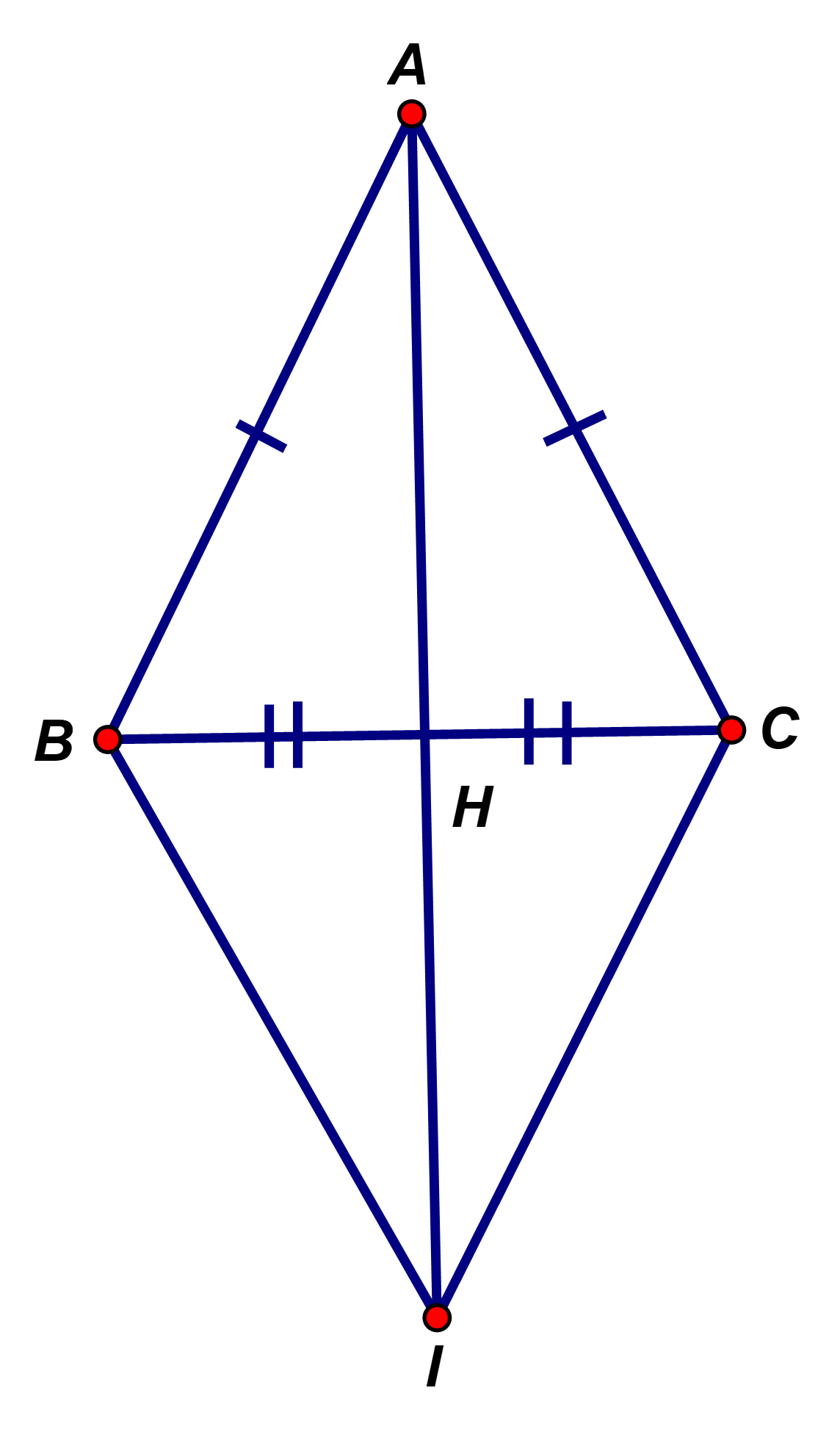
và có:
(gt)
(đối đỉnh)
(H là trung điểm BC)
Suy ra: (c-g-c)
Mà và ở vị trí so le trong
Nên
Câu 12:
Chứng minh
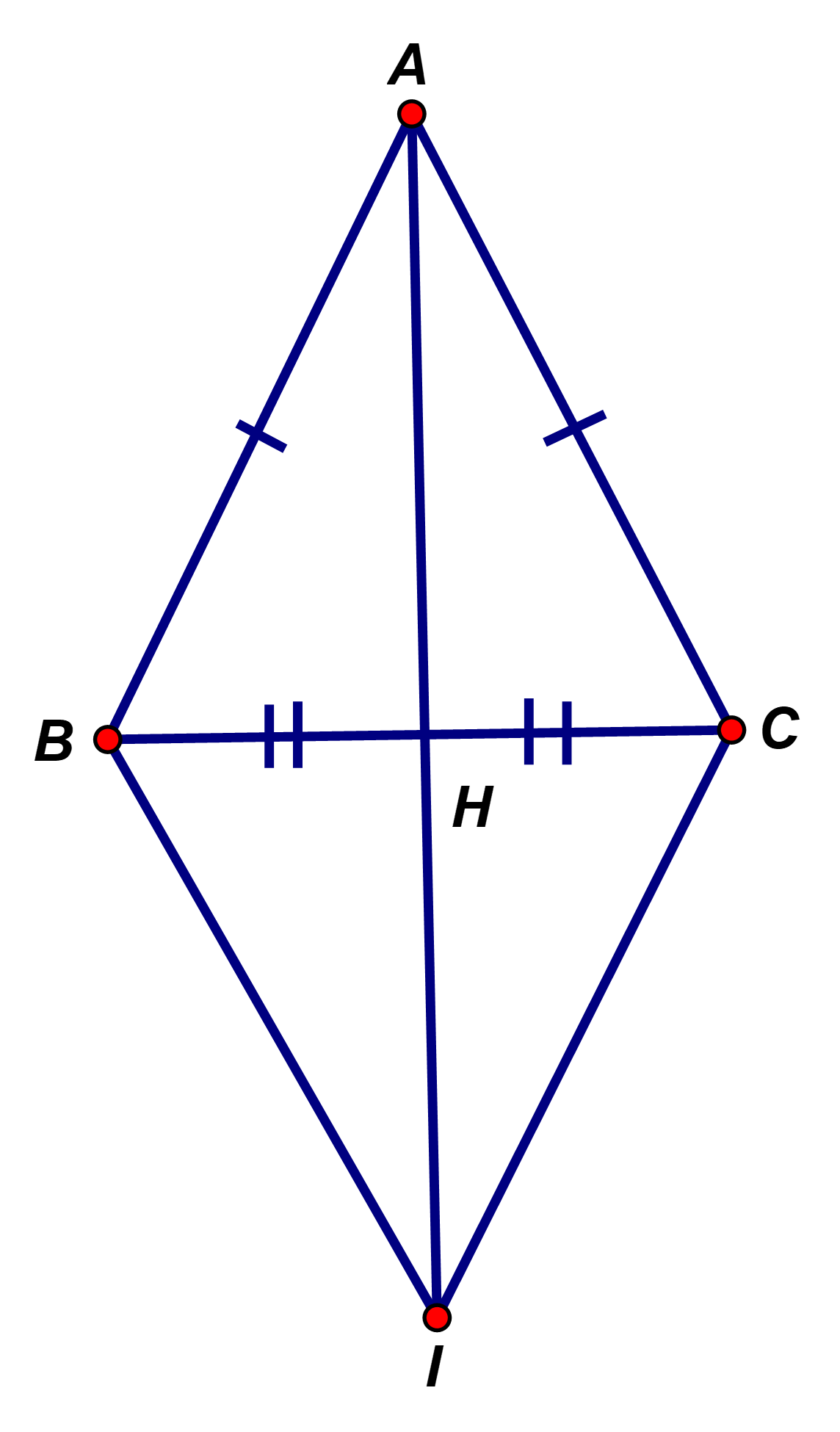
Ta có: (do )
Mà (chứng minh trên)
Nên
