13 câu hỏi trắc nghiệm thuộc Đề kiểm tra học kì 1 Toán 7 có đáp án ( Mới nhất)_ Đề số 1

Câu 1:

Trong các phân số sau, phân số nào biểu diễn số hữu tỉ $- \frac{3}{4}$ ?

A. $\frac{- 6}{2}$

B. $\frac{8}{- 6}$

C. $\frac{9}{- 12}$

D. $\frac{- 12}{9}$

Xem đáp án

Rút gọn các phân số ở các đáp án A, B, C, D, ta được:

A. $\frac{- 6}{2} = - 3$

B. $\frac{8}{- 6} = \frac{- 4}{3}$

C. $\frac{9}{- 12} = - \frac{3}{4}$

D. $\frac{- 12}{9} = \frac{- 4}{3}$

Vậy chọn C. $\frac{9}{- 12}$ .

Câu 2:

Kết quả phép tính $\frac{- 3}{8} + \frac{5}{6}$ là:

A. $\frac{11}{24}$

B. $\frac{22}{48}$

C. $\frac{- 11}{24}$

D. $\frac{- 22}{48}$

Xem đáp án

Ta có: $\frac{- 3}{8} + \frac{5}{6} = \frac{- 9}{24} + \frac{20}{24} = \frac{- 9 + 20}{24} = \frac{11}{24}$ .

Đáp án A

Câu 3:

Cho biết x và y là hai đại lượng tỉ lệ thuận, khi x = 5 thì y = 15. Hệ số tỉ lệ k của y đối với x là:

A. 3

B. 75

C. $\frac{1}{3}$

D. 10.

Xem đáp án

Công thức liên hệ của hai đại lượng x, y tỉ lệ thuận: y = k . x (với k là hệ số tỉ lệ).

Do đó $k = \frac{y}{x} = \frac{15}{5} = 3$ .

Đáp án A

Câu 4:

Nếu góc xOy có số đo bằng 47^o thì số đo của góc đối đỉnh với góc xOy bằng bao nhiêu?

A. 133^o

B. 43^o

C. 74^o

D. 47^o

Xem đáp án

Dựa vào tính chất: Hai góc đối đỉnh thì bằng nhau.

Ta có góc xOy có số đo bằng 47^o nên góc đối đỉnh với góc xOy cũng có số đo bằng 47^o.

Đáp án D

Câu 5:

Cho hình vẽ sau:

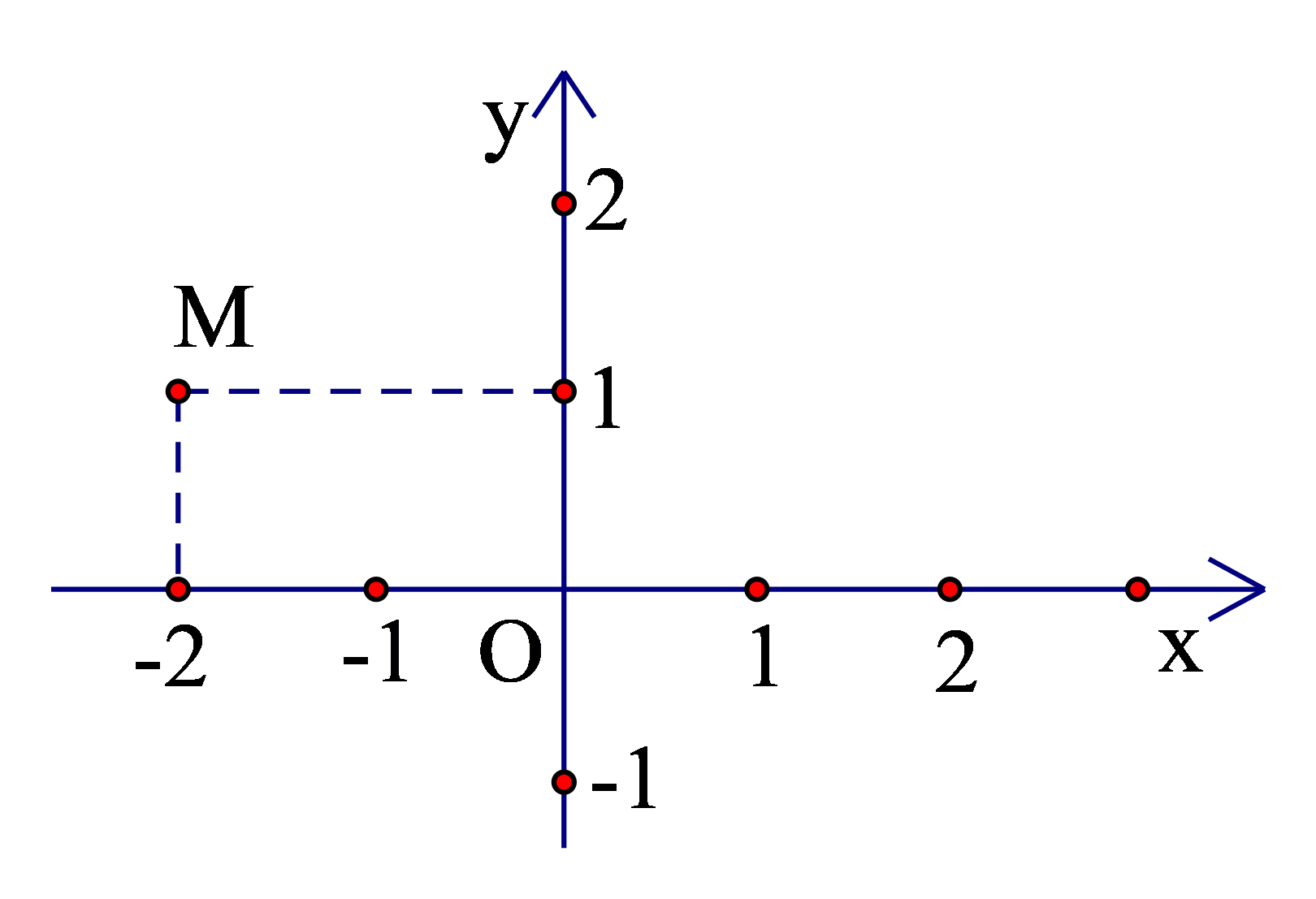
Tọa độ điểm M là:

A. (2; −1)

B. (−2; 1)

C. (1; −2)

D. (−1; 2)

Xem đáp án

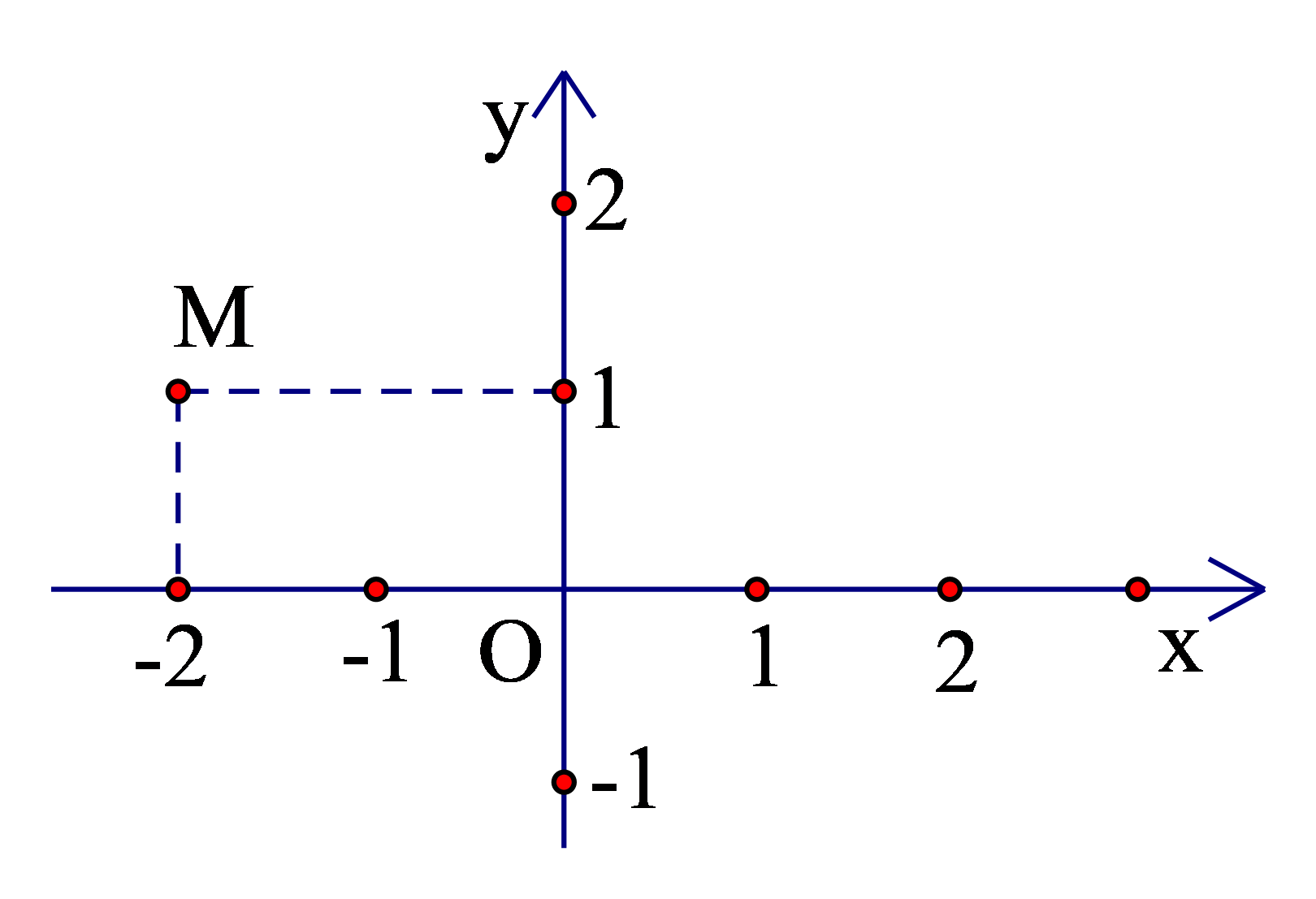
Dựa vào đồ thị hàm số, ta thấy điểm M có hoành độ bằng −2 và tung độ bằng 1.

Do đó, điểm M (−2; 1).

Đáp án B

Câu 6:

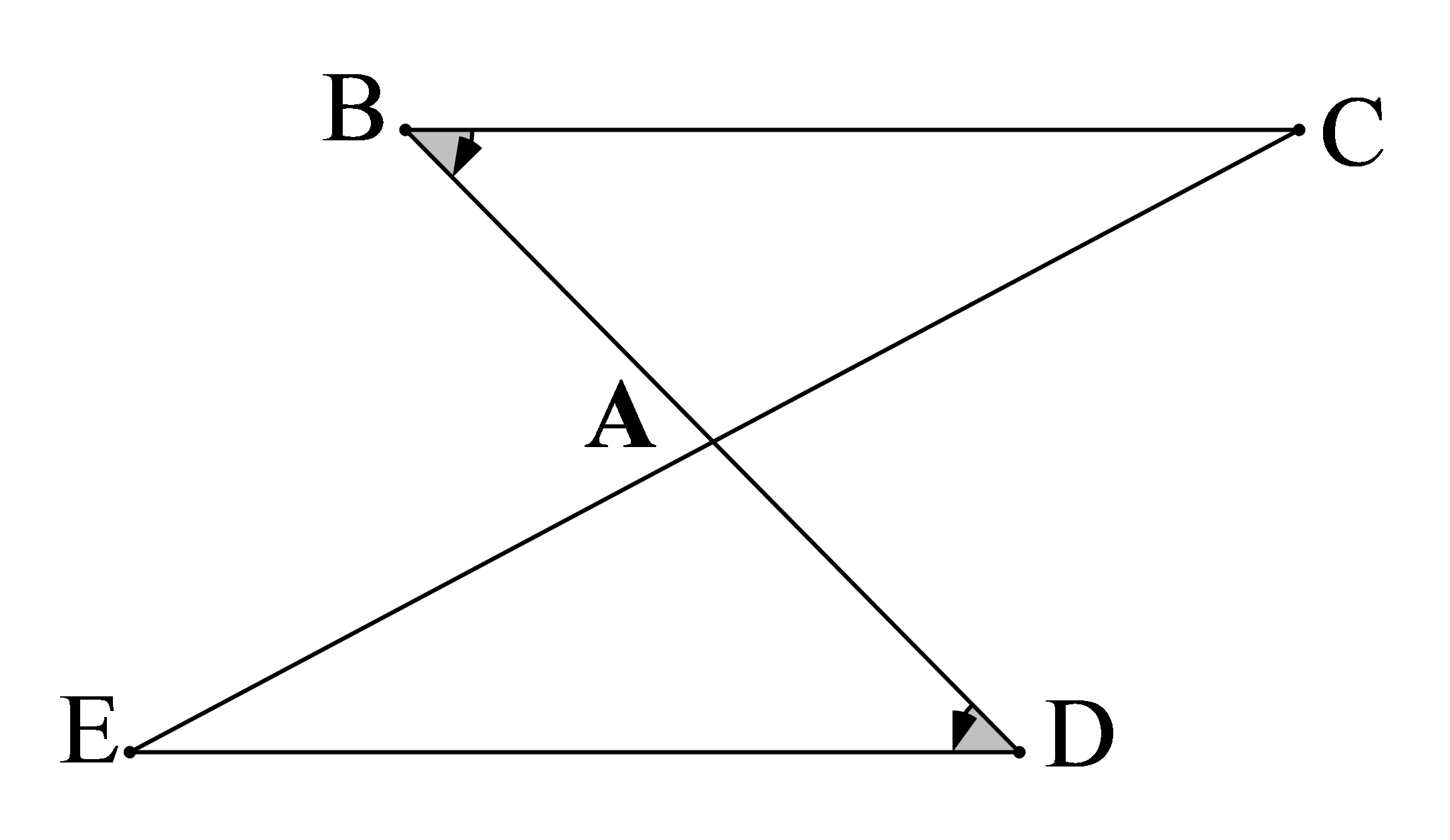
Với các kí hiệu trên hình vẽ, cần có thêm yếu tố nào nữa để kết luận ∆ABC = ∆ADE (g.c.g) ?

A. BC = DE

B. AB = AD

C. AC = AE

D. $\hat{BCA} = \hat{DEA}$ .

Xem đáp án

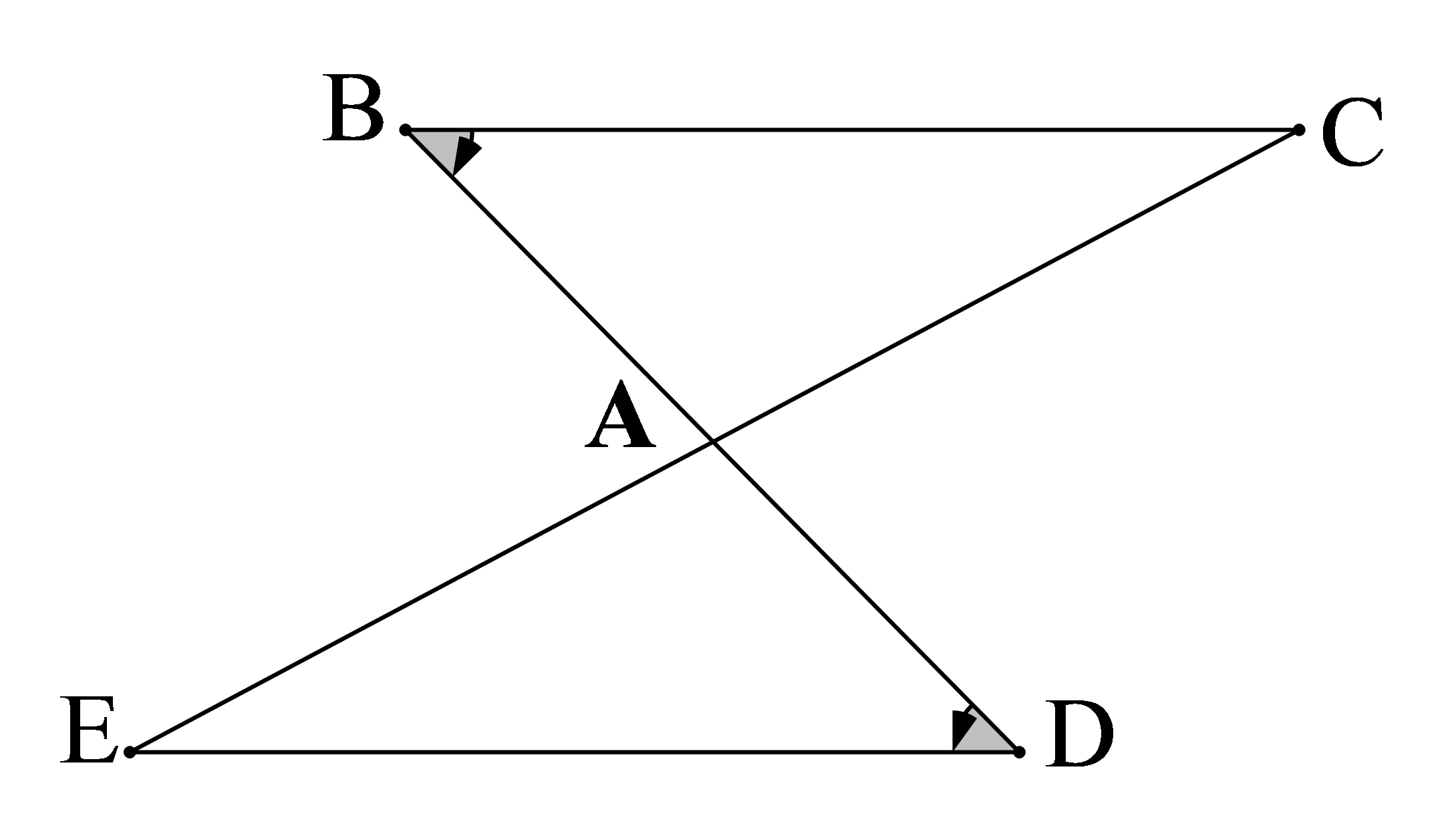
Trong hình vẽ trên có $\hat{ABC} = \hat{ADC}$

Ta lại có $\hat{BAC} = \hat{DAE}$ (hai góc đối đỉnh).

Để ∆ABC = ∆ADE (g.c.g) thì ta cần tìm thêm một điều kiện về cạnh thỏa mãn:

+ Cạnh xen giữa hai góc: Cạnh AB xen giữa hai góc $\hat{ABC}$ và $\hat{BAC}$ ; cạnh AD xen giữa hai góc $\hat{ADC}$ và $\hat{DAE}$ .

+ Hai cạnh đó (thuộc hai tam giác) bằng nhau: Cạnh AB thuộc ∆ABC và cạnh AD thuộc ∆ADE.

Do đó, AB = AD.

Câu 7:

Thực hiện phép tính (tính bằng cách hợp lý nếu có thể)

a) $- 1 \frac{1}{2} . 21 \frac{1}{3} + 1 \frac{1}{2} . 1 \frac{1}{3}$

b) $\frac{{(- 2)}^{3}}{5} . | \frac{1}{4} - 1 | + 2018^{0}$ .

Xem đáp án

a) $- 1 \frac{1}{2} . 21 \frac{1}{3} + 1 \frac{1}{2} . 1 \frac{1}{3}$

$= - 1 \frac{1}{2} . (21 \frac{1}{3} - 1 \frac{1}{3})$

$= - 1 \frac{1}{2} . 20$ = −30.

b) $\frac{{(- 2)}^{3}}{5} . | \frac{1}{4} - 1 | + 2018^{0}$

$= \frac{- 8}{5} . | \frac{- 3}{4} | + 1$

$= \frac{- 8}{5} . \frac{3}{4} + 1$

$= \frac{- 6}{5} + 1 = \frac{- 1}{5}$

Câu 8:

Tìm x, biết:

a) $(0,5 x - \frac{3}{7}) : \frac{1}{2} = 1 \frac{1}{7}$

b) |2 − 3x| − 5 = −1

c) ${(\frac{1}{5} - \frac{3}{2} x)}^{2} = \frac{9}{4}$ .

Xem đáp án

a) $(0,5 x - \frac{3}{7}) : \frac{1}{2} = 1 \frac{1}{7}$

$0,5 x - \frac{3}{7} = 1 \frac{1}{7} . \frac{1}{2}$

$0,5 x - \frac{3}{7} = \frac{8}{7} . \frac{1}{2}$

$0,5 x - \frac{3}{7} = \frac{4}{7}$

$0,5 x = \frac{4}{7} + \frac{3}{7}$

0,5x = 1

x = 1 : 0,5

x = 2.

Vậy x = 2.

b) |2 − 3x| − 5 = −1

|2 − 3x| = 5 −1

|2 − 3x| = 4

Trường hợp 1: 2 − 3x = 4

3x = 2 − 4

3x = −2

$x = \frac{- 2}{3}$ .

Trường hợp 2: 2 − 3x = −4

3x = 2 + 4

3x = 6

x = 2.

Vậy $x \in {\frac{- 2}{3}; 2}$ .

c) ${(\frac{1}{5} - \frac{3}{2} x)}^{2} = \frac{9}{4} {(\frac{1}{5} - \frac{3}{2} x)}^{2} = \frac{9}{4}$

Trường hợp 1: $\frac{3}{2} x = \frac{1}{5} - \frac{3}{2}$

$\frac{3}{2} x = \frac{2}{10} - \frac{15}{10}$

$\frac{3}{2} x = \frac{- 13}{10}$

$x = \frac{- 13}{10} : \frac{3}{2}$

$x = \frac{- 13}{15}$ .

Trường hợp 2: $\frac{1}{5} - \frac{3}{2} x = - \frac{3}{2}$

$\frac{3}{2} x = \frac{1}{5} + \frac{3}{2}$

$\frac{3}{2} x = \frac{17}{10}$

$x = \frac{17}{10} : \frac{3}{2}$

$x = \frac{17}{15}$ .

Vậy $x \in {\frac{- 13}{15}; \frac{17}{15}}$ .

Câu 9:

Một tam giác có chu vi bằng 36cm, ba cạnh của tam giác đó lần lượt tỉ lệ thuận với 3; 4; 5. Tính độ dài ba cạnh của tam giác đó.

Xem đáp án

Gọi độ dài ba cạnh của tam giác là a, b, c (cm) (a, b, c > 0).

Chu vi của tam giác bằng 36 cm nên ta có: a + b + c = 36.

Giả sử ba cạnh tỉ lệ thuận với 3; 4; 5 lần lượt là a, b, c.

Khi đó: $\frac{a}{3} = \frac{b}{4} = \frac{c}{5}$ .

Áp dụng tính chất của dãy tỉ số bằng nhau ta có:

$\frac{a}{3} = \frac{b}{4} = \frac{c}{5} = \frac{a + b + c}{3 + 4 + 5} = \frac{36}{12} = 3$

$\Rightarrow$ a = 3 . 3 = 9;

$\Rightarrow$ b = 3 . 4 = 12;

$\Rightarrow$ c = 3 . 5 = 15.

Vậy độ dài ba cạnh của tam giác là: 9 cm; 12 cm; 15 cm.

Câu 10:

Cho góc nhọn xOy. Trên tia Ox lấy điểm A, B sao cho OA = 3 cm, OB = 5cm. Trên tia Oy lấy điểm C, D sao cho OC = OA, OD = OB. Nối AD và BC cắt nhau tại I.

a) Chứng minh: ∆OAD = ∆OCB.

b) Chứng minh: IA = IC.

c) Chứng minh: OI là tia phân giác của $\hat{x O y}$ .

Xem đáp án

a) Chứng minh: ∆OAD = ∆OCB.

Ta có: OA + AB = OB

OC + CD = OD

Mà OA = OC = 3cm, OD = OB = 5cm.

Nên AB = CD.

Xét ∆OAD và ∆OCB có:

OD = OB (gt)

$\hat{A O D}$ chung

OA = OC (gt).

Do đó ∆OAD = ∆OCB (c.g.c).

b) Chứng minh: IA = IC.

∆OAD = ∆OCB (câu a)

Suy ra: $\hat{O C B} = \hat{O A D}$ , $\hat{O B C} = \hat{O D A}$ (các cặp góc tương ứng).

Ta có: $\hat{O C B} + \hat{B C D} = 180^{o}$

$\hat{O A D} + \hat{B A D} = 180^{o}$

Mà $\hat{O C B} = \hat{O A D}$

Do đó: $\hat{B C D} = \hat{B A D}$ .

Xét ∆ICD và ∆IAB có:

$\hat{O B C} = \hat{O D A}$ (cmt)

CD = AB (cmt)

$\hat{B C D} = \hat{B A D}$ (cmt)

Do đó ∆ICD = ∆IAB (g.c.g).

Suy ra IA = IC (hai cạnh tương ứng).

c) Chứng minh: OI là tia phân giác của $\hat{x O y}$ .

Xét ∆OIC và ∆OAI có:

OC = OA (gt)

IC = IA (cmt)

Cạnh OI chung

Do đó ∆OIC = ∆OAI (c.c.c).

Suy ra: $\hat{I O D} = \hat{I O B}$ (hai góc tương ứng).

Vậy OI là tia phân giác của $\hat{x O y}$ .

Câu 11:

Cho góc nhọn xOy. Trên tia Ox lấy điểm A, B sao cho OA = 3 cm, OB = 5cm. Trên tia Oy lấy điểm C, D sao cho OC = OA, OD = OB. Nối AD và BC cắt nhau tại I.

a) Chứng minh: ∆OAD = ∆OCB.

b) Chứng minh: IA = IC.

c) Chứng minh: OI là tia phân giác của $\hat{x O y}$ .

Xem đáp án

a) Chứng minh: ∆OAD = ∆OCB.

Ta có: OA + AB = OB

OC + CD = OD

Mà OA = OC = 3cm, OD = OB = 5cm.

Nên AB = CD.

Xét ∆OAD và ∆OCB có:

OD = OB (gt)

$\hat{A O D}$ chung

OA = OC (gt).

Do đó ∆OAD = ∆OCB (c.g.c).

b) Chứng minh: IA = IC.

∆OAD = ∆OCB (câu a)

Suy ra: $\hat{O C B} = \hat{O A D}$ , $\hat{O B C} = \hat{O D A}$ (các cặp góc tương ứng).

Ta có: $\hat{O C B} + \hat{B C D} = 180^{o}$

$\hat{O A D} + \hat{B A D} = 180^{o}$

Mà $\hat{O C B} = \hat{O A D}$

Do đó: $\hat{B C D} = \hat{B A D}$ .

Xét ∆ICD và ∆IAB có:

$\hat{O B C} = \hat{O D A}$ (cmt)

CD = AB (cmt)

$\hat{B C D} = \hat{B A D}$ (cmt)

Do đó ∆ICD = ∆IAB (g.c.g).

Suy ra IA = IC (hai cạnh tương ứng).

c) Chứng minh: OI là tia phân giác của $\hat{x O y}$ .

Xét ∆OIC và ∆OAI có:

OC = OA (gt)

IC = IA (cmt)

Cạnh OI chung

Do đó ∆OIC = ∆OAI (c.c.c).

Suy ra: $\hat{I O D} = \hat{I O B}$ (hai góc tương ứng).

Vậy OI là tia phân giác của $\hat{x O y}$ .

Câu 12:

Cho góc nhọn xOy. Trên tia Ox lấy điểm A, B sao cho OA = 3 cm, OB = 5cm. Trên tia Oy lấy điểm C, D sao cho OC = OA, OD = OB. Nối AD và BC cắt nhau tại I.

a) Chứng minh: ∆OAD = ∆OCB.

b) Chứng minh: IA = IC.

c) Chứng minh: OI là tia phân giác của $\hat{x O y}$ .

Xem đáp án

a) Chứng minh: ∆OAD = ∆OCB.

Ta có: OA + AB = OB

OC + CD = OD

Mà OA = OC = 3cm, OD = OB = 5cm.

Nên AB = CD.

Xét ∆OAD và ∆OCB có:

OD = OB (gt)

$\hat{A O D}$ chung

OA = OC (gt).

Do đó ∆OAD = ∆OCB (c.g.c).

b) Chứng minh: IA = IC.

∆OAD = ∆OCB (câu a)

Suy ra: $\hat{O C B} = \hat{O A D}$ , $\hat{O B C} = \hat{O D A}$ (các cặp góc tương ứng).

Ta có: $\hat{O C B} + \hat{B C D} = 180^{o}$

$\hat{O A D} + \hat{B A D} = 180^{o}$

Mà $\hat{O C B} = \hat{O A D}$

Do đó: $\hat{B C D} = \hat{B A D}$ .

Xét ∆ICD và ∆IAB có:

$\hat{O B C} = \hat{O D A}$ (cmt)

CD = AB (cmt)

$\hat{B C D} = \hat{B A D}$ (cmt)

Do đó ∆ICD = ∆IAB (g.c.g).

Suy ra IA = IC (hai cạnh tương ứng).

c) Chứng minh: OI là tia phân giác của $\hat{x O y}$ .

Xét ∆OIC và ∆OAI có:

OC = OA (gt)

IC = IA (cmt)

Cạnh OI chung

Do đó ∆OIC = ∆OAI (c.c.c).

Suy ra: $\hat{I O D} = \hat{I O B}$ (hai góc tương ứng).

Vậy OI là tia phân giác của $\hat{x O y}$ .

Câu 13:

Tìm x, y biết: $\frac{1 + 3 y}{12} = \frac{1 + 5 y}{5 x} = \frac{1 + 7 y}{4 x}$ .

Xem đáp án

ĐK: x $\neq$ 0.

Ta có: $\frac{1 + 3 y}{12} = \frac{1 + 5 y}{5 x} = \frac{1 + 7 y}{4 x}$ (*)

Suy ra: $\frac{1 + 3 y}{12} = \frac{1 + 5 y}{5 x}$ và $\frac{1 + 5 y}{5 x} = \frac{1 + 7 y}{4 x}$ .

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

$\frac{1 + 3 y}{12} = \frac{1 + 5 y}{5 x}$ $= \frac{1 + 3 y - (1 + 5 y)}{12 - 5 x} = \frac{1 + 3 y - 1 - 5 y}{12 - 5 x} = \frac{- 2 y}{12 - 5 x}$ (1)

$\frac{1 + 5 y}{5 x} = \frac{1 + 7 y}{4 x} = \frac{1 + 5 y - (1 + 7 y)}{5 x - 4 x} = \frac{1 + 5 y - 1 - 7 y}{5 x - 4 x} = \frac{- 2 y}{x}$

(2)

Từ (1) và (2) suy ra: $\frac{- 2 y}{12 - 5 x}$ = $\frac{- 2 y}{x}$ (3)

- Nếu y = 0 thay vào (*), ta được: $\frac{1}{12} = \frac{1}{5 x} = \frac{1}{4 x}$

Mà x 0 nên không có giá trị x thỏa mãn (*).

- Nếu y 0:

Từ (3) suy ra: x = 12 – 5x

x + 5x = 12

6x = 12

x = 2 (thỏa mãn)

Thay x = 2 vào (*) ta được:

$\frac{1 + 3 y}{12} = \frac{1 + 5 y}{10} = \frac{1 + 7 y}{8}$

$\Rightarrow \frac{1}{12} + \frac{1}{4} y = \frac{1}{10} + \frac{1}{2} y$

$\Rightarrow \frac{1}{4} y = \frac{- 1}{60}$

$\Rightarrow y = \frac{- 1}{15}$ (thỏa mãn)

Vậy x = 2, $y = \frac{- 1}{15}$ thoả mãn yêu cầu bài toán.

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đề kiểm tra học kì 1 Toán 7 có đáp án ( Mới nhất)

Đề kiểm tra học kì 1 Toán 7 có đáp án ( Mới nhất)_ Đề số 1

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương