Bài tập chuyên đề Toán 7 Dạng 7: Các trường hợp bằng nhau của tam giác vuông có đáp án
Bài tập chuyên đề Toán 7 Dạng 7: Các trường hợp bằng nhau của tam giác vuông có đáp án
-
296 lượt thi
-
19 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
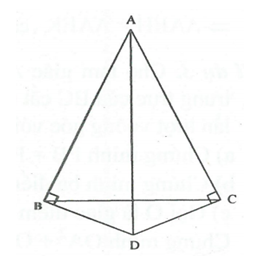
* Tìm cách giải. Để chứng minh AD là tia phân giác của góc BAC, chúng ta cần chứng minh . Do đó hiển nhiên cần chứng minh
* Trình bày lời giải.
Xét và có: ; AD là cạnh chung; (cân tại A).
Do đó (cạnh huyền - cạnh góc vuông)
(cặp góc tương ứng).
Vậy AD là tia phân giác góc BAC.
* Nhận xét. Chúng ta còn có DA là tia phân giác của góc BDC, tam giác DBC cân tại D.
AD vuông góc với BC.
Câu 2:
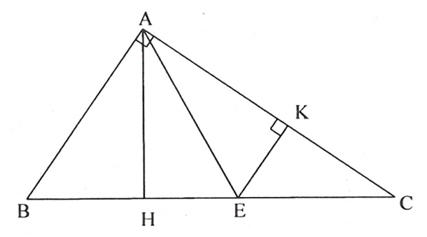
* Trình bày lời giải.
cân tại B nên (vì cùng vuông góc với AC)
(slt) .
Câu 3:
Cho tam giác ABC (AB < AC), M là trung điểm của BC. Đường trung trực của BC cắt tia phân giác của góc BAC tại điểm P. Vẽ PH và PK lần lượt vuông góc với đường thẳng AB và đường thẳng AC.
a) Chứng minh PB = PC và BH = CK.
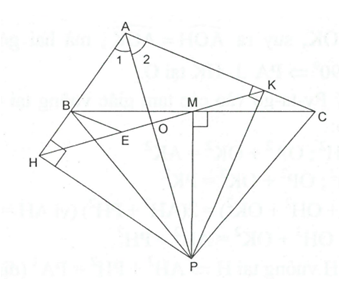
a) và có
, MP là cạnh chung
(hai cạnh tương ứng)
Câu 4:
b) và có , AP là cạnh chung
(cạnh huyền - góc nhọn)
(hai cạnh tương ứng)
và có
(cạnh huyền - cạnh góc vuông)
(hai cạnh tương ứng)
Câu 5:
c) Gọi O là giao điểm của PA và HK.
Chứng minh
c) và có là cạnh chung
, suy ra , mà hai góc này kề bù nên
tại O.
Áp dụng định lý Py-ta-go vào các tam giác vuông tại O là OAH, OAK, OPH, OPK ta có:
(vì và )
Mà tam giác PAH vuông tại H (định lý Py-ta-go)
Câu 6:
Cho tam giác ABC cân tại A. Trên cạnh BC lấy D, E (D nằm giữa B và E) sao choBD=CE. Vẽ tại M, tại N. Gọi K là giao điểm của MD và NE. Chứng minh rằng:
a,
Hướng dẫn:
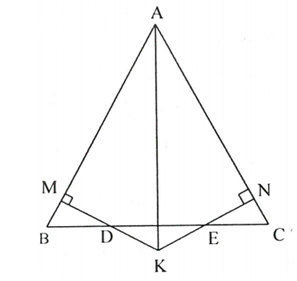
a) Xét và có: ;
. Do đó
(cạnh huyền – góc nhọn) .Câu 7:
b, Chứng minh rằng:
b) (chứng minh trên)
nên
Xét và có: ;
AK là cạnh chung; AM = AN.
Do đó (cạnh huyền – cạnh góc vuông).
Câu 8:
Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD=CE. Kẻ tại H, kẻ tại K.
Chứng minh rằng: a,
a)
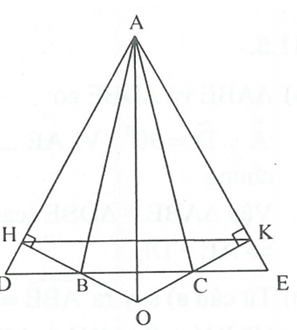
Ta có mà
và có
(c.g.c)
và có ;
(cạnh huyền – góc nhọn).
Câu 11:
Cho tam giác ABC có M là trung điểm của BC, AM là tia phân giác góc A. Kẻ MH vuông góc với AB; MK vuông góc với AC. Chứng minh rằng: a,

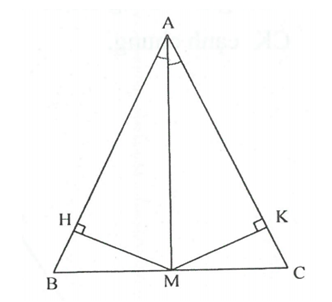
a) và có: ;
AM chung;
(cạnh huyền góc nhọn)
.
Câu 13:
a)
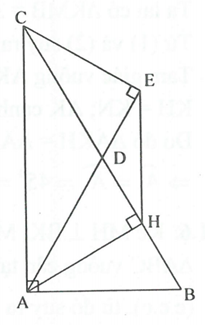
(c.g.c), suy ra AB = AD.
vuông tại A, có nên .
Tam giác ABD cân, có nên là tam giác đều.
Câu 14:
b)
(cạnh huyền – góc nhọn)
Suy ra CH = AE.
cân tại vì nên DA = DC.
Suy ra hay . Do đó cân tại D, hai tam giác cân DAC và DEH có góc ở đỉnh
.
Câu 15:
Cho tam giác ABC vuông tại A. Trên cạnh BC lấy điểm D sao cho BD= BA . Qua D vẽ đường thẳng vuông góc với BC cắt AC tại E.
a) Chứng minh rằng:.
a)
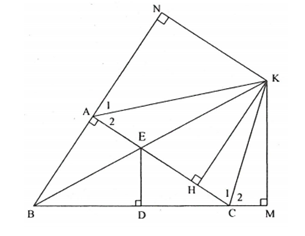
và có:
(Vì )
AB=AD (giả thiết), BE: cạnh chung
Vậy (ch-cgv)
.
Câu 16:
b) Từ câu a) suy ra , do đó BK là phân giác của góc ABC.
Vẽ .
Tam giác vuông KMC và tam giác vuông KHC có: (giả thiết); CK cạnh chung.
Do đó (cạnh huyền – góc nhọn), suy ra (1)
Ta lại có (cạnh huyền – góc nhọn) nên (2)
Từ (1) và (2) suy ra
Tam giác vuông AKH và tam giác vuông AKN có cạnh chung.
Do đó (cạnh huyền – cạnh góc vuông)Câu 17:
Cho tam giác ABC có và M là trung điểm của BC. Trên tia đối của tia CB lấy điểm D. Kẻ BK vuông góc với đường thẳng AD tại K.
Chứng minh rằng KM là tia phân giác của .
Hướng dẫn
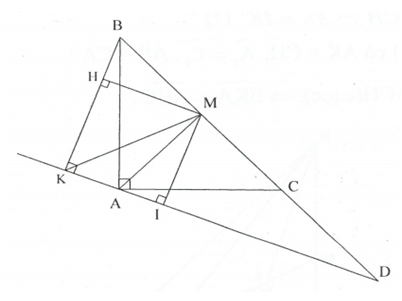
Kẻ vuông cân tại A có MB= MC nên dễ dàng suy ra (c.c.c), từ đó suy ra
Ta có:
và có
,
(cạnh huyền – góc nhọn)
.
và có , MK chung; MH = MI
(cạnh huyền – cạnh góc vuông)
Vậy KM là tia phân giác
Câu 18:
Cho tam giác ABC vuông cân đáy BC. Gọi M, N là trung điểm của AB, AC. Kẻ tại H, kẻ tại E. Chứng minh rằng:
a)
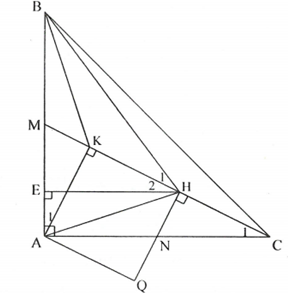
Từ A kẻ tại K và tại Q.
Hai tam giác vuông MAK và NCH có
(cùng phụ với góc AMC)
(1)
và có AK = CH, , AB = CA
và có AN = NC,
(2)
Từ (1) và (2), suy ra: AK = AQ.
và có chung
là tia phân giác của góc KHQ
Từ
Tam giác AKH có nên nó vuông cân tại K suy ra KA = KH.
hay cân tại B.
Câu 19:
b) Dễ chứng minh được và
Mà (góc đồng vị) vì .
Hay HM là tia phân giác góc BHE.
