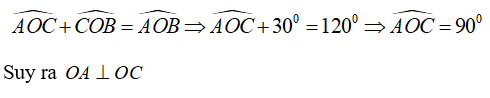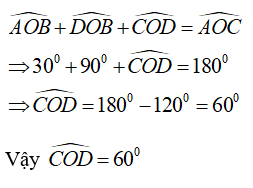Bài tập: Hai đường thẳng vuông góc có đáp án
-
2217 lượt thi
-
17 câu hỏi
-
15 phút
Danh sách câu hỏi
Câu 1:
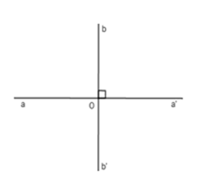
Chọn hai đường thẳng aa' và bb' vuông góc với nhau tại O. Hãy chỉ ra câu sai trong các câu sau:
Hai đường thẳng aa' và bb' vuông góc với nhau tại nên:
+ ∠aOb = 90° nên B đúng.
+ aa' và bb' vuông góc với nhau nên aa' và bb' cắt nhau nên C sai.
+ ∠a'Ob = ∠ a'Ob' = 90° ⇒ aa' là đường phân giác của góc bẹt bOb' nên D đúng.
+ ∠b'Oa' = 90° nên A đúng.
Chọn đáp án C.
Câu 2:
Hãy chọn câu đúng trong các câu sau:
Hai đường thẳng vuông góc thì cắt nhau
Chọn đáp án B.
Câu 3:
Đường trung trực của một đoạn thẳng là:
Đường trung trực của một đoạn thẳng là đường vuông góc với đoạn thẳng ấy tại trung điểm của nó.
Chọn đáp án D.
Câu 4:
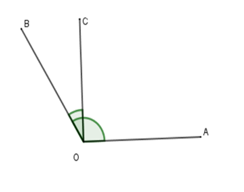
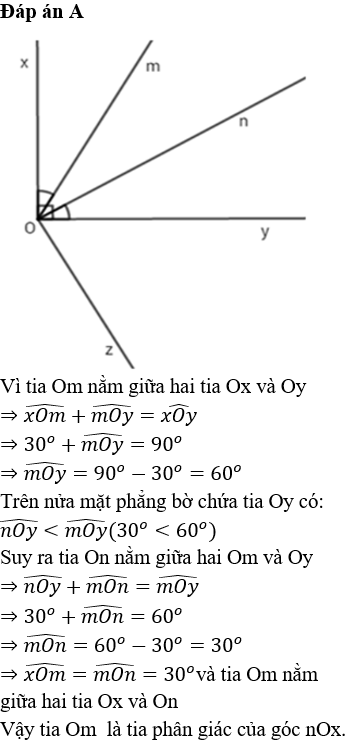
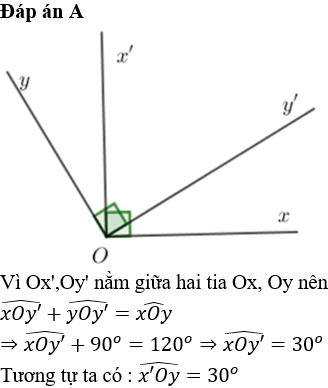
Cho ∠AOB = 120°. Tia OC nằm giữa hai tia OA, OB sao cho ∠BOC = 30°. Chọn câu đúng:
Vì OC nằm giữa hai tia OA, OB nên
Chọn đáp án A.
Câu 5:
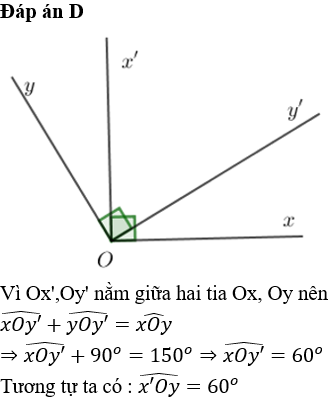
Cho ∠AOB = 30°. Vẽ tia OC là tia đối của tia OA. Tính ∠COD biết OD vuông góc OB, các tia OD và OA thuộc hai nửa mặt phẳng đối nhau bờ OB
Vì OD vuông góc OB nên ∠DOB = 90°
Vì OA và OC là hai tia đối nhau và tia OB nằm giữa OA và OD nên ta có:
Chọn đáp án D.
Câu 6:
Khi đường thẳng AB vuông góc với đường thẳng CD, ta kí hiệu:
Khi đường thẳng AB vuông góc với đường thẳng CD, ta kí hiệu AB ⊥ CD
Chọn đáp án D
Câu 7:
Chọn phát biểu đúng
Tính chất thừa nhận: Có một và chỉ một đường thẳng d’ đi qua điểm O và vuông góc với đường thẳng d cho trước. (Phần lý thuyết)
Suy ra A đúng
B diễn đạt tương tự theo tính chất trên, nên đáp án B cũng đúng.
Vậy cả A và B đều đúng.
Chọn đáp án C
Câu 8:
Cho đoạn thẳng MN = 6 cm. Trên tia MN lấy điểm P sao cho MP = 1 cm, trên tia NM lấy điểm Q sao cho NQ = 1 cm. Khi đó:
+ Trên tia MN có:
MN = 6 cm; MP = 1 cm
Suy ra P nằm giữa M và N (do 6 > 1)
⇒ MP + PN = MN ⇒ PN = MN – MP = 6 – 1 = 5 cm
+ Trên tia NM có:
NM = 6 cm; NQ = 1 cm
Suy ra Q nằm giữa M và N (do 6 > 1)
⇒ NQ + QM = NM ⇒ QM = NM – NQ = 6 – 1 = 5 cm
Do đó: PN = QM (= 5 cm) A đúng
+ Gọi A là trung điểm của đoạn thẳng MN ⇒ AM = AN = 1/2 MN = 3 cm
Gọi d là đường thẳng đi qua A và vuông góc với MN tại A
Do đó d là đường trung trực của đoạn thẳng MN
Vì P và Q đều thuộc MN, nên suy ra d ⊥ PQ (1) ⇒ B đúng
+ Trên tia MN có MA = 3 cm; MP = 1 cm
Suy ra P nằm giữa M và A ⇒ MP + PA = MA ⇒ PA = MA – MP = 3 – 1 = 2 cm
Chứng minh tương tự ta có: NQ + QA = NA ⇒ QA = NA – NQ = 3 – 1 = 2 cm
Do đó: PA = QA, mà P, Q, A thẳng hàng (do P, Q, A đều thuộc MN)
Suy ra A là trung điểm của PQ (2)
Từ (1) và (2) suy ra d là đường trung trực của đoạn thẳng PQ ⇒ C đúng
Chọn đáp án D
Câu 9:
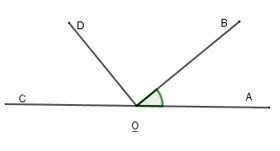
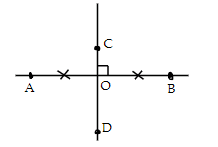
Cho hình vẽ sau, hãy chọn câu sai trong các câu sau
Quan sát hình vẽ đã cho ta thấy
+ AO = OB (D đúng) ⇒ O là trung điểm của AB (1)
+ CD ⊥ AB tại O (2) ⇒ 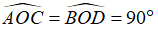
Từ (1) và (2) suy ra CD là đường trung trực của đoạn thẳng AB ⇒ A đúng
+ Vì OC ≠ OD suy ra AB không phải là đường trung trực của CD ⇒ B sai
Chọn đáp án B
Câu 10:
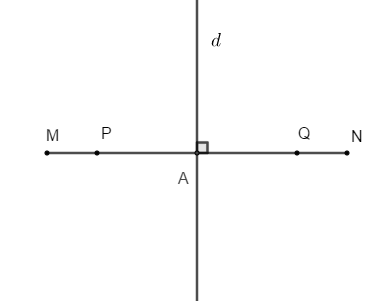
Cho đường thẳng d và điểm O thuộc đường thẳng d. Vẽ đường thẳng d’ đi qua O và vuông góc với d. Chọn hình vẽ đúng trong các hình vẽ dưới đây.
Vì điểm O thuộc đường thẳng d, suy ra đáp án A và D thỏa mãn, loại B và C
Đường thẳng d’ đi qua O và vuông góc với d, suy ra A đúng, D sai
Chọn đáp án A