Đề kiểm tra Giữa kì 2 Toán 7 có đáp án (Mới nhất) - Đề 2
-
1286 lượt thi
-
8 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Ta thấy đơn thức xy2 đồng dạng với đơn thức 5xy2 vì đơn thức xy2 có hệ số là 1 ≠ 0 và có cùng phần biến là xy2.
Vậy chọn D.
Câu 2:
∆ABC có \(\widehat A = {90^o}\) và AB = AC nên ∆ABC là tam giác vuông cân tại A.
Vậy chọn C.
Câu 3:
Đơn thức là biểu thức đại số chỉ gồm một số, một biến hoặc một tích giữa các số và các biến.
Do đó, các biểu thức 4x2y ; 6xy.(−x3) ; −4xy2 là các đơn thức
Còn biểu thức 7 + xy2 có chứa phép cộng nên không phải là đơn thức.
Vậy chọn B.
Câu 4:
Ta có, góc đối diện với cạnh AB là \(\widehat C\); góc đối diện với cạnh AC là \(\widehat B\); góc đối diện với cạnh BC là \(\widehat A\).
Vì AB < AC < BC nên \(\widehat C\) < \(\widehat B\) < \(\widehat A\) (quan hệ giữa góc và cạnh đối diện trong một tam giác).
Chọn đáp án A
Câu 5:
Điểm kiểm tra môn toán của học sinh lớp 7A được thống kê như sau:
|
7 |
10 |
5 |
7 |
8 |
10 |
6 |
5 |
7 |
8 |
|
7 |
6 |
4 |
10 |
3 |
4 |
9 |
8 |
9 |
9 |
|
4 |
7 |
3 |
9 |
2 |
3 |
7 |
5 |
9 |
7 |
|
5 |
7 |
6 |
4 |
9 |
5 |
8 |
5 |
6 |
3 |
a) Dấu hiệu ở đây là gì?
b) Hãy lập bảng “tần số”.
c) Hãy tính số trung bình cộng và tìm mốt của dấu hiệu?
d) Nhận xét về việc học toán của học sinh lớp 7A.
a) Dấu hiệu: Điểm kiểm tra môn toán của mỗi học sinh lớp 7A.
b) Bảng “tần số”:
|
Giá trị (x) |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
Tần số (n) |
1 |
4 |
4 |
6 |
4 |
8 |
4 |
6 |
3 |
N = 30 |
c) Số trung bình cộng:
\(\overline X = \frac{{2\,.\,1 + 3\,.\,4 + 4\,.\,4 + 5\,.\,6 + 6\,.\,4 + 7\,.\,8 + 8\,.\,4 + 9\,.\,6 + 10\,.\,3}}{{30}} \approx \,\,8,53\) (điểm).
Giá trị có tần số lớn nhất là 7 (tần số của giá trị 7 là 8).
Do đó một của dấu hiệu là Mo = 7.
Vậy số trung bình cộng là \(\overline X \approx \,\,8,53\) điểm và mốt của dấu hiệu là Mo = 7.
d) Nhận xét về việc học toán của học sinh lớp 7A:
- Số các giá trị của dấu hiệu: 30.
- Số các giá trị khác nhau của dấu hiệu: 9.
- Điểm cao nhất là 10 điểm; điểm thấp nhất là 2 điểm.
- Giá trị có tần số lớn nhất là 7 (tần số của giá trị 7 là 8).
- Các giá trị thuộc vào khoảng 5 điểm; 7 điểm và 9 điểm.
Câu 6:
Tính giá trị của biểu thức 2x4 − 5x2 + 4x tại x = 1 và \(x = \frac{{ - 1}}{2}\).
Thay x = 1 vào giá trị biểu thức 2x4 − 5x2 + 4x, ta được:
2.14 – 5.12 + 4.1 = 2 – 5 + 4 = 1.
Thay \(x = \frac{{ - 1}}{2}\) vào giá trị biểu thức 2x4 − 5x2 + 4x, ta được:
\(2\,.\,{\left( {\frac{{ - 1}}{2}} \right)^4} - 5\,.\,{\left( {\frac{{ - 1}}{2}} \right)^2}\, + \,4\,.\,\left( {\frac{{ - 1}}{2}} \right) = - \frac{{25}}{8}\).
Vậy giá trị của biểu thức đã cho tại x = 1 và \(x = \frac{{ - 1}}{2}\) lần lượt là 1 và \( - \frac{{25}}{8}\).
Câu 7:
Cho ΔABC vuông tại A. Đường phân giác BD. Vẽ DH ⊥ BC
(H ∈ BC).
a) Chứng minh: ΔABD = ΔHBD.
b) Chứng minh: AD < DC.
c) Trên tia đối AB lấy điểm K sao cho AK = HC. Chứng minh ΔDKC cân.|
GT |
ΔABC vuông tại A, đường phân giác BD; DH ⊥ BC (H ∈ BC); Trên tia đối AB lấy điểm K sao cho AK = HC. |
|
KL |
a) ΔABD = ΔHBD. b) AD < DC. c) ΔDKC cân. |
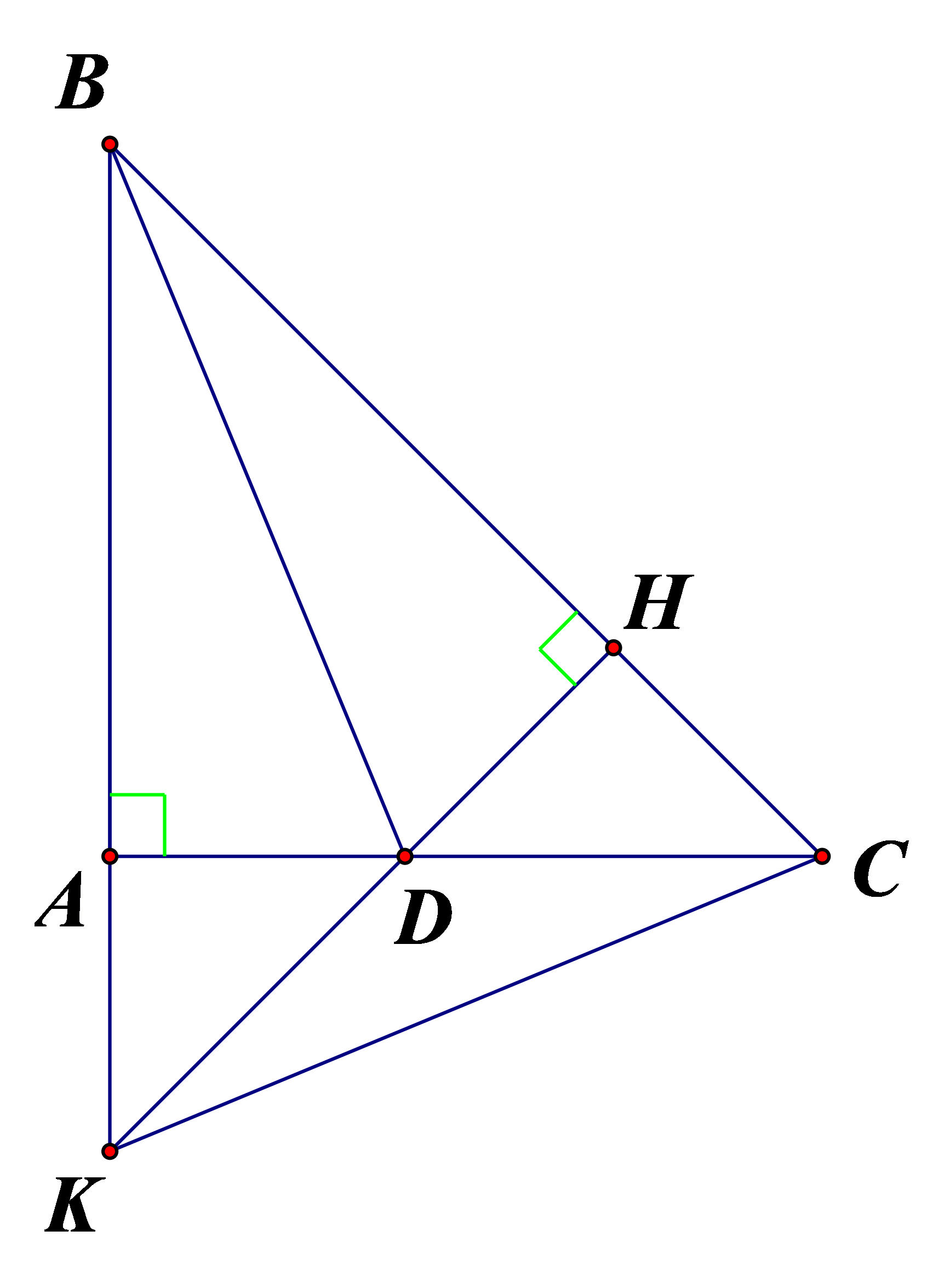
a) Xét ΔABD và ΔHBD có:
\(\widehat {BAD} = \widehat {BHD} = {90^o}\)
\(\widehat {ABD} = \widehat {HBD}\) (vì BD là tia phân giác của \(\widehat {ABC}\)).
Cạnh BD chung.
Do đó ΔABD = ΔHBD (cạnh huyền – góc nhọn).
b) Từ câu a: ΔABD = ΔHBD suy ra AD = DH (hai cạnh tương ứng) (1)
ΔDHC vuông tại H nên DH < DC (2) (trong tam giác vuông cạnh đối diện với góc vuông là cạnh lớn nhất).
Từ (1) và (2) suy ra: AD < DC.
c) Xét ΔAKD và ΔHCD có:
\(\widehat {DAK} = \widehat {CHD} = {90^o}\)
AD = DH (cmt)
\[\widehat {ADK} = \widehat {CDH}\] (hai góc đối đỉnh)
Do đó ΔAKD = ΔHCD (c.g.c).
Suy ra KD = DC (hai cạnh tương ứng).
Vậy ΔDKC cân tại D.Câu 8:
Cho \(A = \frac{{5n + 1}}{{n + 1}}\) (n ≠ −1). Tìm \(n \in \mathbb{Z}\) để biểu thức A đạt giá trị nguyên.
Với n ≠ −1, ta có: \[A = \frac{{5n + 1}}{{n + 1}} = \frac{{5(n + 1) - 4}}{{n + 1}} = 5 - \frac{4}{{n + 1}}\].
Để biểu thức A đạt giá trị nguyên thì \[5 - \frac{4}{{n + 1}} \in \mathbb{Z}\].
Mà \[5 \in \mathbb{Z}\] nên \[\frac{4}{{n + 1}} \in \mathbb{Z}\] hay 4 \[ \in \] Ư(4) = {−1; 1; −4; 4}.
Ta có bảng sau:
|
n + 1 |
−1 |
1 |
−4 |
4 |
|
n |
−2 (TM) |
0 (TM) |
−5 (TM) |
3 (TM) |
Vậy để biểu thức A đạt giá trị nguyên thì x \[ \in \]{−5; −2; 0; 3}.