Đề kiểm tra Giữa kì 2 Toán 7 có đáp án (Mới nhất) - Đề 1
-
1818 lượt thi
-
8 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
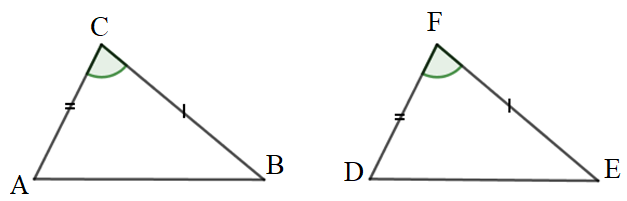
Để ∆ABC = ∆DEF (c.g.c), khi biết hai cặp cạnh bằng nhau là: AC = DF, BC = EF.
Ta cần thêm điều kiện cặp góc xen giữa bằng nhau là \[\widehat C = \widehat F\].
Vậy chọn D.
Câu 2:
- Thay x = 0 vào đồ thị hàm số ta được: f(0) = (−3).0 = 0 ≠ −3.
Do đó điểm A(0; −3) không thuộc đồ thị hàm số y = f(x) = −3x.
- Thay x = −2 vào đồ thị hàm số ta được: f(−2) = (−3). (−2) = 6.
Do đó điểm B(−2; 6) thuộc đồ thị hàm số y = f(x) = −3x.
- Thay x = 1 vào đồ thị hàm số ta được: f(1) = (−3). 1 = −3 ≠ 3.
Do đó điểm C(1; 3) không thuộc đồ thị hàm số y = f(x) = −3x.
- Thay x = 5 vào đồ thị hàm số ta được: f(5) = (−3). 5 = −15 ≠ 15.
Do đó điểm D(5; 15) không thuộc đồ thị hàm số y = f(x) = −3x.
Vậy chọn B.
Câu 3:
Bậc của đa thức là bậc cao nhất của hạng tử.
Hạng tử 3a5 có bậc cao nhất là 5.
Do đó bậc của đa thức đã cho là 5.
Vậy chọn A.
Câu 4:
Áp dụng định lý Py-ta-go vào ∆ABC vuông tại A, ta có:
AB2 + AC2 = BC2
\[ \Rightarrow BC = \sqrt {A{B^2} + A{C^2}} = \sqrt {{{18}^2} + {{24}^2}} = 30\] (cm)
Do đó chu vi tam giác ABC là:
AB + AC + BC = 18 + 24 + 30 = 72 (cm).
Vậy chọn C.
Câu 5:
II. Tự luận:
Điểm thi học kỳ I môn Sinh học của các bạn học của lớp 7A được thống kê trong bảng “tần số” sau:
|
Điểm (x) |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
Tần số (n) |
3 |
4 |
4 |
8 |
5 |
7 |
1 |
N = 32 |
a) Tìm mốt của dấu hiệu trong bảng “tần số “trên? Giải thích tại sao?
b) Tính điểm trung bình của lớp 7A.
c) Nêu nhận xét.
a) Mốt của dấu hiệu: 7.
Vì tần số của điểm 7 là lớn nhất (tần số của điểm 7 là 8).
b) Điểm trung bình cộng:
\(\overline X = \frac{{4\,.\,3 + 5\,.\,4 + 6\,.\,4 + 7\,.\,8 + 8\,.\,5 + 9\,.\,7 + 10\,.\,1}}{{32}} \approx 7,03\).
Vậy điểm trung bình học kỳ I môn Sinh học của lớp 7A là 7,03.
c) Nhận xét:
- Số các giá trị của dấu hiệu là 32.
- Số các giá trị khác nhau là 7.
- Giá trị lớn nhất là 10; giá trị nhỏ nhất là 4.
- Giá trị có tần số lớn nhất 7 (tần số của giá trị 7 là 8).
- Các giá trị thuộc vào khoảng 7 điểm đến 9 điểm là chủ yếu.
Câu 6:
Cho đơn thức .
a) Thu gọn đơn thức A.
b) Xác định hệ số và bậc của đơn thức A.
c) Tính giá trị của A khi x = 1; y = −1; z = 2.
a) Ta có: \[A = \left( {\frac{{ - 1}}{2}{x^2}{y^3}z} \right)\,\,.\,\,\left( {\frac{{ - 14}}{3}x{y^2}{z^2}} \right)\]
\[ = \left( {\frac{{ - 1}}{2}\,.\,\,\frac{{ - 14}}{3}} \right).\,\left( {{x^2}.\,x} \right).\,\left( {{y^3}.\,{y^2}} \right)\left( {z\,.\,{z^2}} \right)\]
\[ = \frac{7}{3}\,.\,{x^{2\, + \,1}}.\,\,{y^{3\, + \,2}}.\,{z^{1\, + \,2}}\]
\[ = \frac{7}{3}{x^3}{y^5}{z^3}\].
Vậy \[A = \frac{7}{3}{x^3}{y^5}{z^3}\].
b) Đơn thức A có hệ số là \[\frac{7}{3}\].
Đơn thức \[\frac{7}{3}{x^3}{y^5}{z^3}\], biến x có số mũ là 3; biến y có số mũ là 5; biến z có số mũ là 3.
Tổng số mũ của các biến là 3 + 5 + 3 = 11.
Vậy đơn thức A có hệ số là \[\frac{7}{3}\] và có bậc là 11.
c) Thay x = 1; y = −1; z = 2 vào biểu thức A, ta được:
\[A = \frac{7}{3}{x^3}{y^5}{z^3} = \frac{7}{3}\,.\,{1^3}\,.\,{( - 1)^5}\,.\,{2^3} = - \frac{{56}}{3}\].
Câu 7:
Cho tam giác ABC vuông tại A, \[\widehat B = {60^o}\], AB = 5cm. Tia phân giác góc B cắt AC tại D. Từ D kẻ đường thẳng vuông góc với BC tại E.
a) Chứng minh: ∆ADB = ∆BDE.
b) Chứng minh tam giác AEB là tam giác đều.
c) Tính BC.
|
GT |
∆ABC vuông tại A, \[\widehat B = {60^o}\], AB = 5cm. BD là tia phân giác \(\widehat {ABC}\) (\(D \in AC\)). \(DE \bot BC\,\,(E \in BC)\). |
|
KL |
a) ∆ADB = ∆BDE. b) ∆AEB là tam giác đều. c) Tính BC. |
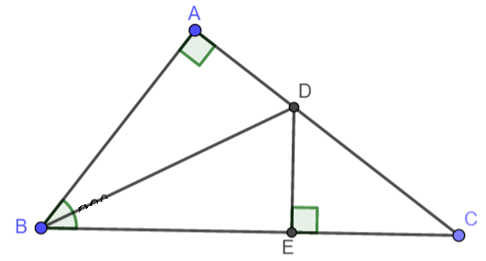
a) Xét ∆ABD vuông tại A và ∆BDE vuông tại E có:
BD cạnh chung.
\[\widehat {ABD} = \widehat {DBE} = {30^o}\](BD là phân giác góc B)
Do đó ∆ADB = ∆BDE (cạnh huyền – góc nhọn).
b) Từ câu a: ∆ADB = ∆BDE suy ra AB = BE.
Xét ∆ABE có AB = BE, \(\widehat B = {60^o}\).
Vậy ∆ABE là tam giác đều.
c) Ta có ∆ABE là tam giác đều (câu b)
Suy ra AB = BE = AE = 5 cm (*)
Do đó \[\widehat {BAE} = \widehat {ABE} = {60^o}\]
Mặt khác \[\widehat {BAC} = {90^o}\]
\[ \Rightarrow \widehat {EAC} = \widehat {BAC} - \widehat {BAE} = {90^o} - {60^o} = {30^o}\] (1)
Áp dụng định lý tổng ba góc của một tam giác vào ∆ABC, ta có:
\[\widehat {ABC} + \widehat {BCA} + \widehat {BAC} = {180^o}\]
\[ \Rightarrow \widehat {BCA} = {180^o} - \widehat {ABC} - \widehat {BAC}\]
\[ \Rightarrow \widehat {BCA} = {180^o} - {60^o} - {90^o} = {30^o}\] (2)
Từ (1) và (2) suy ra \[\widehat {EAC} = \widehat {BCA}\] nên ∆AEC cân tại E.
Suy ra AC = EC = 5 cm (**)
Từ (*) và (**) suy ra BC = BE + EC = 5 + 5 = 10 (cm).
Vậy BC = 10 cm.
Câu 8:
Tìm các giá trị nguyên của x và y biết: 5y – 3x = 2xy – 11.
Ta có: 5y – 3x = 2xy – 11
2xy – 11 – 5y + 3x = 0
2 . (2xy – 11 – 5y + 3x) = 0 . 2
4xy – 22 – 10y + 6x = 0
4xy + 6x – 10y – 15 – 7 = 0
(4xy + 6x) – (10y + 15) = 7
2x(2y + 3) – 5(2y + 3) = 7
(2x – 5)(2y + 3) = 7
Ta có bảng sau:
|
2x – 5 |
1 |
7 |
–1 |
–7 |
|
2y + 3 |
7 |
1 |
–7 |
–1 |
|
x |
3 |
6 |
2 |
–1 |
|
y |
2 |
–1 |
–5 |
–2 |
Vậy có các cặp số (x; y) là: (3; 2), (6; –1), (2; –5), (–1; –2).