Trắc nghiệm Toán 7 KNTT Bài 8: Góc ở vị trí đặc biệt. Tia phân giác của một góc có đáp án
Trắc nghiệm Toán 7 KNTT Dạng 3. Tính số đo các góc dựa vào tính chất góc ở vị trí đặc biệt, định nghĩa tia phân giác có đáp án
-
674 lượt thi
-
14 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Cho hai đường thẳng xt và yz cắt nhau tại A sao cho \(\widehat {xAy} = 5{5^o}\). Hãy tính số đo các góc sau:
\(\widehat {xAz}\);
Hướng dẫn giải:
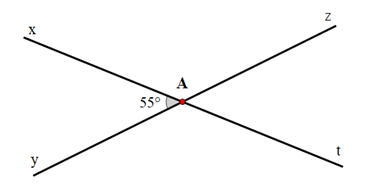
Suy ra \[\widehat {xAz} = {180^o} - \widehat {xAy} = {180^o} - {55^o} = {125^o}\];
Câu 2:
Cho hai đường thẳng xt và yz cắt nhau tại A sao cho \(\widehat {xAy} = 5{5^o}\). Hãy tính số đo các góc sau:
\(\widehat {zAt}\);
Hướng dẫn giải:
Vì \(\widehat {xAy}\) và \(\widehat {zAt}\) là hai góc đối đỉnh nên \(\widehat {zAt} = \widehat {xAy} = 5{5^o}\);
Câu 3:
Cho hai đường thẳng xt và yz cắt nhau tại A sao cho \(\widehat {xAy} = 5{5^o}\). Hãy tính số đo các góc sau:
\(\widehat {yAt}\).
Hướng dẫn giải:
Hướng dẫn giải:
Vì \(\widehat {xAz}\) và \(\widehat {yAt}\) là hai góc đối đỉnh nên \(\widehat {yAt} = \widehat {xAz} = 12{5^o}\).
Câu 4:
Hướng dẫn giải:
Vì Oz là tia phân giác của \(\widehat {xOy}\) nên:
\(\widehat {xOz}\) = \(\widehat {zOy}\) = \(\frac{{\widehat {xOy}}}{2} = \frac{{{{150}^o}}}{2} = {75^o}\).
Câu 5:
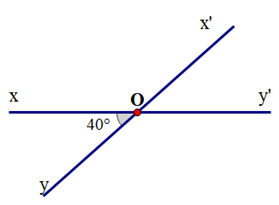
Cho hình vẽ sau. Số đo \(\widehat {xOx'}\) là:
Hướng dẫn giải:
Đáp án đúng là: C
Vì \(\widehat {xOy},\,\,\widehat {xOx'}\) là hai góc kề bù nên \(\widehat {xOy} + \widehat {xOx'} = 18{0^o}\).
Suy ra \(\widehat {xOx'} = 18{0^o} - \widehat {xOy} = 18{0^o} - 4{0^o} = 14{0^o}\).
Câu 6:
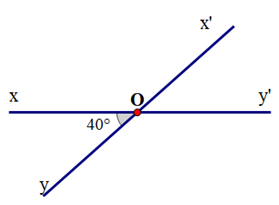
Cho hình vẽ sau. Số đo \(\widehat {{\rm{x'Oy}}'}\) là:
Hướng dẫn giải:
Đáp án đúng là: A
Vì \(\widehat {{\rm{xOy}}}{\rm{,}}\widehat {{\rm{x'Oy'}}}\) là hai góc đối đỉnh nên \(\widehat {xOy} = \widehat {x'Oy'} = {40^o}\).
Vậy \(\widehat {x'Oy'} = {40^o}\).
Câu 7:
Cho \(\widehat {xOy} = {30^o}\); Oy là tia phân giác \(\widehat {xOz}\). Khi đó \(\widehat {xOz}\) bằng:
Hướng dẫn giải:
Đáp án đúng là: B
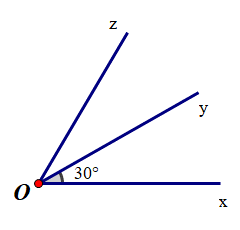
Vì Oy là tia phân giác \(\widehat {xOz}\) nên \(\widehat {xOy} = \frac{{\widehat {xOz}}}{2}\).
Suy ra \(\widehat {xOz} = 2.\widehat {xOy} = {2.30^o} = {60^o}\).
Câu 8:
Ot là tia phân giác của \(\widehat {xOy}\) khi:
Hướng dẫn giải:
Đáp án đúng là: C
Vì \(\widehat {xOt} = \widehat {yOt} = \frac{1}{2}\widehat {xOy}\) nên \(\widehat {xOt} + \widehat {tOy} = \frac{1}{2}\widehat {xOy} + \frac{1}{2}\widehat {xOy} = \widehat {xOy}\).
Hay \(\widehat {xOt} + \widehat {tOy} = \widehat {xOy}\) .
Suy ra tia Ot nằm giữa hai tia Ox và Oy.
Mà \(\widehat {xOt} = \widehat {tOy}\).
Do đó tia Ot là tia phân giác của \(\widehat {xOy}\).
Câu 9:
Hướng dẫn giải:
Đáp án đúng là: C
Tia phân giác của một góc là tia nằm giữa hai cạnh của một góc và tạo với hai cạnh ấy hai góc bằng nhau.
Câu 10:
Cho \(\widehat {xOy}\)
và \(\widehat {yOz}\) là hai góc kề bù. Biết \(\widehat {xOy}\) = 60° và tia Ot là tia phân giác của \(\widehat {yOz}\). Số đo góc \(\widehat {xOt}\) là:
Hướng dẫn giải:
Đáp án đúng là: D
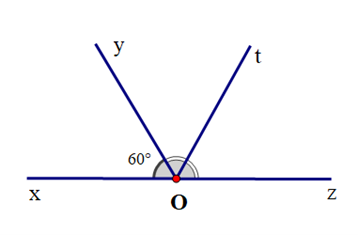
Vì \(\widehat {xOy}\)
và \(\widehat {yOz}\) là hai góc kề bù nên \(\widehat {xOy}\) + \(\widehat {yOz}\) = 180°.
Suy ra \(\widehat {yOz}\) = 180° − \(\widehat {xOy}\) = 180° − 60° = 120°.
Mà Ot là tia phân giác của \(\widehat {yOz}\) nên:
\(\widehat {tOz} = \frac{1}{2}\widehat {yOz} = \frac{1}{2}{.120^o} = {60^o}\).
Vì \(\widehat {xOt}\)và \(\widehat {tOz}\) là hai góc kề bù nên \(\widehat {xOt}\) + \(\widehat {tOz}\) = 180°.
Suy ra \(\widehat {xOt}\) = 180° − \(\widehat {tOz}\) = 180° − 60° = 120° .
Câu 11:
Cho hai đường thẳng xx’ và yy’ cắt nhau tại O sao cho \(\widehat {xOy} = {60^o}\). Gọi Ot là tia phân giác của \(\widehat {x'Oy}'\). Số đo \(\widehat {xOt}\) là:
Hướng dẫn giải:
Đáp án đúng là: A
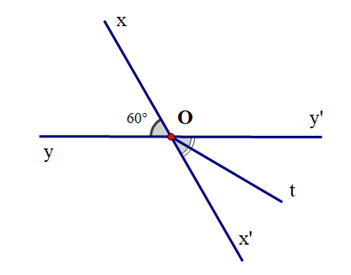
Vì \(\widehat {x'Oy}'\) và \(\widehat {xOy}\) là hai góc đối đỉnh nên \(\widehat {x'Oy}'\) = \(\widehat {xOy}\) = 60°.
Do Ot là tia phân giác của \(\widehat {x'Oy}'\) nên:
\(\widehat {x'Ot} = \frac{1}{2}\widehat {x'Oy'} = \frac{1}{2}{.60^o} = {30^o}\).
Vì \(\widehat {xOt}\) và \(\widehat {x'Ot}\) là hai góc kề bù nên \(\widehat {xOt}\) + \(\widehat {x'Ot}\) = 180°.
Suy ra \(\widehat {xOt}\) = 180° − \(\widehat {x'Ot}\) = 180° − 30° = 150°.
Câu 12:
Hướng dẫn giải:
Đáp án đúng là: A
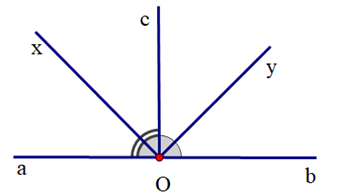
Vì Oc là tia phân giác của \(\widehat {aOb}\) nên \(\widehat {aOc} = \widehat {cOb} = \frac{1}{2}\widehat {aOb}\).
Suy ra \(\widehat {aOc} = \widehat {cOb} = \frac{1}{2}{.180^o} = {90^o}\) (vì \(\widehat {aOb}\) là góc bẹt)
Vì Ox là phân giác của \(\widehat {aOc}\) nên:
\(\widehat {xOc} = \frac{1}{2}\widehat {aOc} = \frac{1}{2}{.90^o} = {45^o}\).
Vì Oy là phân giác của \(\widehat {cOb}\) nên:
\(\widehat {cOy} = \frac{1}{2}\widehat {cOb} = \frac{1}{2}{.90^o} = {45^o}\).
Ta có tia Oc nằm giữa hai tia Ox và Oy nên:
\(\widehat {xOy} = \widehat {xOc} + \widehat {cOy} = {45^o} + {45^o} = {90^o}\).
Vậy \(\widehat {xOy} = {90^o}\).
Câu 13:
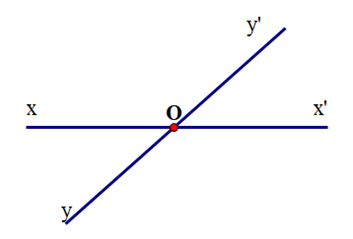
Cho hai đường thẳng xx’ và yy’ cắt nhau như hình vẽ. Biết \(\widehat {xOy'} - \widehat {xOy} = {90^o}\). Tính \(\widehat {xOy}\).
Hướng dẫn giải:
Đáp án đúng là: B
Ta có \(\widehat {xOy'} - \widehat {xOy} = {90^o}\)
Suy ra \(\widehat {xOy'} = \widehat {xOy} + {90^o}\)
Vì \(\widehat {xOy},\widehat {xOy'}\) là hai góc kề bù nên \(\widehat {xOy} + \widehat {xOy'} = {180^o}\)
Suy ra \(\widehat {xOy} + {90^o} + \widehat {xOy} = {180^o}\)
Suy ra \(2\widehat {xOy} = {90^o}\)
Do đó \(\widehat {xOy} = {45^o}\).Câu 14:
Cho hai đường thẳng xx’ và yy’ cắt nhau như hình vẽ. Biết \(\widehat {xOy'} = 2\widehat {xOy}\). Tính \(\widehat {xOy}\).
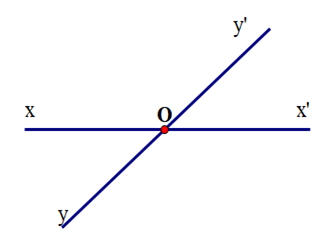
Hướng dẫn giải:
Đáp án đúng là: A
Vì \(\widehat {xOy},\widehat {xOy'}\) là hai góc kề bù nên \(\widehat {xOy} + \widehat {xOy'} = {180^o}\).
Mà \(\widehat {xOy'} = 2\widehat {xOy}\)
Suy ra \(\widehat {xOy} + 2\widehat {xOy} = {180^o}\)
Suy ra \(3\widehat {xOy} = {180^o}\)
Do đó \(\widehat {xOy} = {60^o}\).