6 câu hỏi trắc nghiệm thuộc Đề kiểm tra học kì 1 Toán 7 có đáp án ( Mới nhất)_ Đề số 4

Câu 1:

Thực hiện phép tính (Tính nhanh nếu có thể)

a) $\frac{- 2}{15} + \frac{3}{10}$

b) $9 . {(- \frac{1}{3})}^{2} + \frac{1}{6} . \sqrt{4}$

c) $15 \frac{1}{4} : \frac{5}{7} - 25 \frac{1}{4} : \frac{5}{7}$

Xem đáp án

a) $\frac{- 2}{15} + \frac{3}{10}$

$= \frac{- 4}{30} + \frac{9}{30}$

$= \frac{5}{30} = \frac{1}{6}$

b) $9 . {(- \frac{1}{3})}^{2} + \frac{1}{6} . \sqrt{4}$

$= 9 . \frac{1}{9} + \frac{1}{6} . 2$

$= 1 + \frac{1}{3}$

$= \frac{4}{3}$ .

c) $15 \frac{1}{4} : \frac{5}{7} - 25 \frac{1}{4} : \frac{5}{7}$

$= (15 \frac{1}{4} - 25 \frac{1}{4}) : \frac{5}{7}$

$= - 10 . \frac{7}{5}$ = −14.

Câu 2:

Tìm x, biết:

a) $x - \frac{2}{3} = - \frac{5}{21}$

b) x² + 15 = 20

c) $\frac{2}{3} x = - \frac{5}{21}$ .

Xem đáp án

a) $x - \frac{2}{3} = - \frac{5}{21}$

$x = \frac{2}{3} - \frac{5}{21}$

$x = \frac{14}{21} - \frac{5}{21}$

$x = \frac{3}{7}$ .

Vậy $x = \frac{3}{7}$ .

b) x² + 15 = 20

x² = 20 − 15

x² = 5

$x = \sqrt{5}$ hoặc $x = - \sqrt{5}$

Vậy $x \in {\sqrt{5}; - \sqrt{5}}$ .

c) $\frac{2}{3} x = - \frac{5}{21}$

$x = - \frac{5}{21} : \frac{2}{3}$

$x = - \frac{5}{21} . \frac{3}{2}$

$x = - \frac{5}{14}$

Vậy $x = - \frac{5}{14}$ .

Câu 3:

Ba đơn vị kinh doanh gốp vốn theo tỉ lệ 3; 5; 7. Hỏi mỗi đơn vị chia bao nhiêu lãi nếu tổng số tiền lãi là 450 triệu đồng và tiền lãi được chia tỉ lệ thuận với số vốn đã góp.

Xem đáp án

Gọi a, b, c lần lượt là số tiền lãi của ba đơn vị kinh doanh nhận được (triệu đồng) (0 < a, b, c < 450).

Ta có số tiền lãi tỉ lệ thuận với số vốn đã góp.

Giả sử a, b, c lần lượt tỉ lệ với 3; 5; 7 nên $\frac{a}{3} = \frac{b}{5} = \frac{c}{7}$ .

Tổng số tiền lãi là 450 triệu đồng nên a + b + c = 450.

Áp dụng tính chất dãy tỉ số bằng nhau:

$\frac{a}{3} = \frac{b}{5} = \frac{c}{7} = \frac{a + b + c}{3 + 5 + 7} = \frac{450}{15} = 30$

Do đó: a = 3. 30;

b = 5 . 30 = 150;

c = 7 . 30 = 210.

Vậy số tiền lãi của ba đơn vị nhận được lần lượt là: 90 triệu đồng; 150 triệu đồng và 210 triệu đồng.

Câu 4:

Cho đồ thị của hàm số $y = (m - \frac{1}{2}) x$ (với m là hằng số, $m \neq \frac{1}{2})$ đi qua điểm A (2; 6).

a) Xác định m.

b) Vẽ đồ thị của hàm số đã cho với giá trị m tìm được ở câu a. Tìm trên đồ thị hàm số trên điểm có tung độ bằng 2.

Xem đáp án

a) Hàm số $y = (m - \frac{1}{2}) x$ (với m là hằng số, $m \neq \frac{1}{2})$ đi qua điểm A (2; 6).

Nên: $6 = (m - \frac{1}{2}) . 2$

$m - \frac{1}{2} = 3$

$m = \frac{7}{2}$ .

Vậy $m = \frac{7}{2}$ .

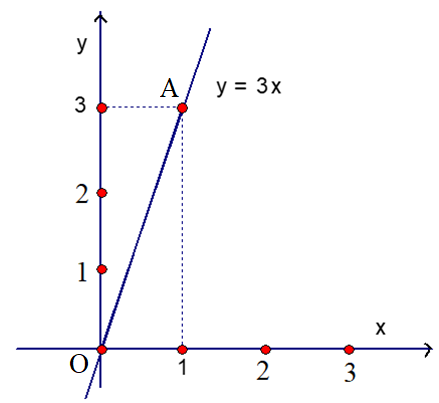
b) Với $m = \frac{7}{2}$ , ta có đồ thị hàm số y = 3x.

* Cách vẽ:

- Vẽ hệ trục tọa độ Oxy.

- Đồ thị hàm số đi qua O (0; 0).

- Với x = 1 ta được y = 1. 3 = 3, điểm A (1; 3) thuộc đồ thị hàm số y = 3x.

Do đó, đường thẳng OA là đồ thị của hàm số đã cho.

* Ta có đồ thị hàm số y = 3x.

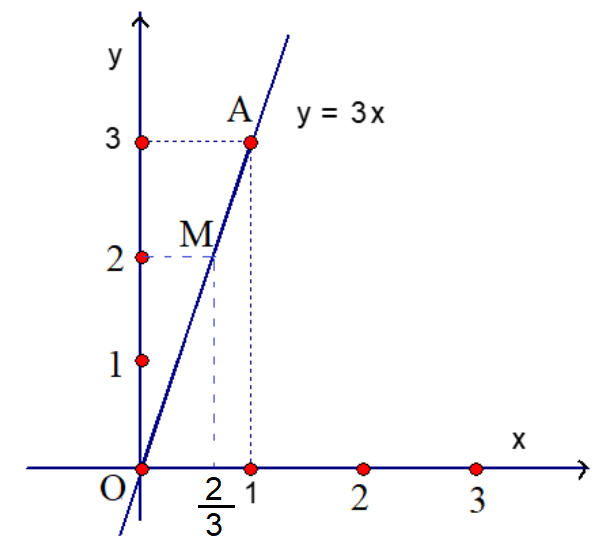
Cho đồ thị của hàm số y=(m-1/2)x (với m là hằng số, m khác 1/2 đi qua điểm A (2; 6). a) Xác định m. b) Vẽ đồ thị của hàm số đã cho với giá trị m tìm được ở câu a. Tìm trên đồ thị hàm số trên điểm có tung độ bằng 2. (ảnh 3)

Điểm có tung độ bằng 2 hay y = 2. Khi đó, $x = \frac{y}{3} = \frac{2}{3}$ .

Do đó, điểm $M (\frac{2}{3}; 2)$ thuộc đồ thị hàm số y = 3x và có tung độ bằng 2 (như hình vẽ).

Câu 5:

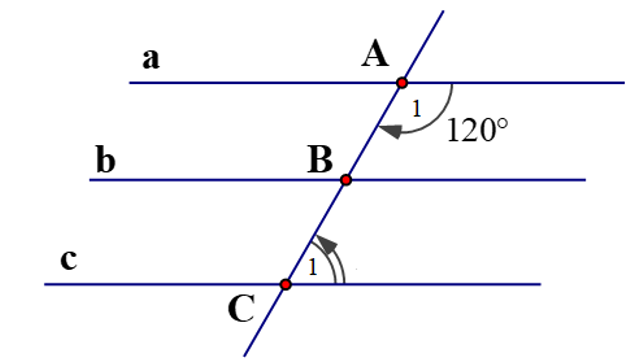
1) Cho hình vẽ sau, biết a // b và b // c. Tính số đo ${\hat{C}}_{1}$ ?

1) Cho hình vẽ sau, biết a // b và b // c. Tính số đo góc C1 ? Cho ∆ABC vuông tại A. Tia phân giác của góc B cắt cạnh AC tại D. Trên cạnh BC lấy điểm H sao cho BH = BA. a) Chứng minh: ∆ABD = ∆HBD. b) Chứng minh: DH vuông góc BC. c) Giả sử góc C=60 độ . Tính số đo góc ADB (ảnh 1)

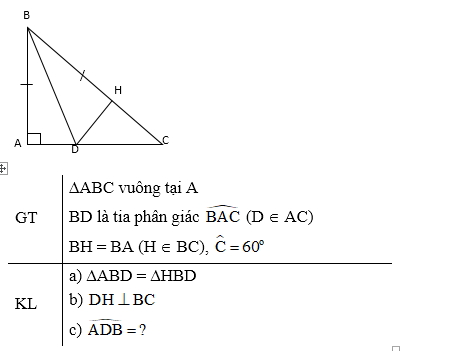
2) Cho ∆ABC vuông tại A. Tia phân giác của góc B cắt cạnh AC tại D. Trên cạnh BC lấy điểm H sao cho BH = BA.

a) Chứng minh: ∆ABD = ∆HBD.

b) Chứng minh: $D H ⊥ B C$ .

c) Giả sử $\hat{C} = 60^{o}$ . Tính số đo $\hat{A D B}$ .

Xem đáp án

1)

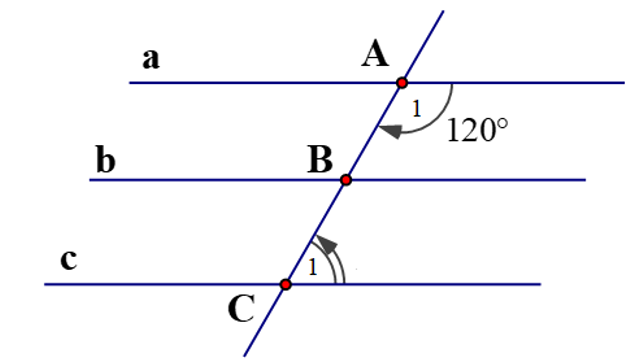
Ta có: a // b và b // c.

Suy ra: a // c (tính chất ba đường thẳng song song).

Ta lại có: ${\hat{A}}_{1}$ và ${\hat{C}}_{1}$ là hai góc trong cùng phía nên ${\hat{A}}_{1} + {\hat{C}}_{1} = 180^{o}$ .

$\Rightarrow {\hat{C}}_{1} = 180^{o} - {\hat{A}}_{1} = 180^{o} - 120^{o} = 60^{o}$ .

Vậy ${\hat{C}}_{1} = 60^{o}$ .

2)

a) Chứng minh: ∆ABD = ∆HBD.

Xét ∆ABD và ∆HBD có:

AB = BH (gt)

$\hat{A B H} = \hat{D B H}$ (vì BD là tia phân giác của $\hat{B A C}$ )

Cạnh BD chung.

Do đó ∆ABD = ∆HBD (c.g.c)

b) Chứng minh: $D H ⊥ B C$

Vì ∆ABD = ∆HBD (câu a) nên $\hat{B A D} = \hat{B H D}$ (hai góc tương ứng)

Mà $\hat{B A D} = 90^{o}$ . Do đó $\hat{B H D}$ = 90^o.

Vậy DH $⊥$ BC.

c) Tính số đo $\hat{A D B}$ .

Ta có ∆ABC vuông tại A nên $\hat{A B C} + \hat{C} = 90^{o}$ .

Mà $\hat{C} = 60^{o}$ nên $\hat{A B C} = 30^{o}$ .

Vì BD là tia phân giác của $\hat{B A C}$ .

Nên $\hat{A B D} = \hat{D B H} = \hat{A B D} : 2 = 30^{o} : 2 = 15^{o}$ .

Ta có ∆ABD vuông tại A nên $\hat{A B D} + \hat{A D B} = 90^{o}$ .

$\hat{A D B} = 90^{o} - \hat{A B D} = 90^{o} - 15^{o} = 75^{o}$

Vậy $\hat{A D B} = 75^{o}$ .

Câu 6:

So sánh 2³⁰+ 3³⁰ + 4³⁰ và 3 . 24¹⁰.

Xem đáp án

Ta có: 4³⁰ = (2 . 2)³⁰ = 2³⁰. 2³⁰ = (2³)¹⁰ . (2²)¹⁵ = 8¹⁰ . 4¹⁵

Lại có: 24¹⁰ . 3 = (8 . 3)¹⁰ . 3 = 8¹⁰ . 3¹⁰. 3 = 8¹⁰ . 3¹¹

Ta thấy 4¹⁵ > 4¹¹ > 3¹¹

Suy ra 8¹⁰ . 4¹⁵ > 8¹⁰ . 3¹¹

Hay 4³⁰ > 3 . 24¹⁰

Do đó 2³⁰+ 3³⁰ + 4³⁰ > 3 . 24¹⁰.

Vậy 2³⁰ + 3³⁰ + 4³⁰ > 3 . 24¹⁰.

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đề kiểm tra học kì 1 Toán 7 có đáp án ( Mới nhất)

Đề kiểm tra học kì 1 Toán 7 có đáp án ( Mới nhất)_ Đề số 4

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương