8 câu hỏi trắc nghiệm thuộc Đề kiểm tra học kì 2 Toán 7 có đáp án ( Mới nhất)_ đề số 6

Câu 1:

Cho đơn thức T = 3x²y³z. Đơn thức nào sau đây sau khi thu gọn đồng dạng với T.

A. x²y²zx.

B. xy²zxy.

C. x²zy²z².

D. x²yxz.

Xem đáp án

Đáp án đúng là: B

Ta có x²y²zx = (x².x).y².z = x³y²z ≠ x²y³z.

xy²zxy = (x.x).(y².y).z = x²y³z.

x²zy²z² = x²y².(z.z²) = x²y²z³≠ x²y³z.

x²yxz = (x².x)yz = x³yz ≠ x²y³z.

Câu 2:

Cho đa thức P(x) = x³ - 6x² + 11x - 6. Giá trị nào sau đây KHÔNG là nghiệm của P(x)?

A. 1.

B. 2.

C. 3.

D. 4.

Xem đáp án

Đáp án đúng là: D

Với x = 1 thì P(1) = 1³ - 6.1² + 11.1 - 6 = 1 - 6 + 11 - 6 = 0.

Do đó x = 1 là nghiệm của P(x).

Với x = 2 thì P(2) = 2³ - 6.2² + 11.2 - 6 = 8 - 6.4 + 22 - 6 = 8 - 24 + 22 - 6 = 0.

Do đó x = 2 là nghiệm của P(x).

Với x = 3 thì P(3) = 3³ - 6.3² + 11.3 - 6 = 27 - 6.9 + 33 - 6 = 27 - 54 + 33 - 6 = 0.

Do đó x = 3 là nghiệm của P(x).

Với x = 4 thì P(4) = 4³ - 6.4² + 11.4 - 6 = 64 - 96 + 44 - 6 = 6 ≠ 0.

Do đó x = 4 là nghiệm của P(x).

Câu 3:

Tam giác ABC có $\hat{A} = 43 °$ và $\hat{B} = 69 °$ . Thứ tự nào sau đây đúng?

A. BC < CA < AB.

B. AB < CA < BC.

C. BC < AB < CA.

D. AB < BC < CA.

Xem đáp án

Đáp án đúng là: C

Xét $Δ A B C$ : $\hat{A} + \hat{B} + \hat{C} = 180 °$ .

Khi đó $\hat{C} = 180 ° - \hat{A} - \hat{B}$ = 180^o - 43^o - 69^o = 68^o.

Do 43^o < 68^o < 69^o nên $\hat{A} < \hat{C} < \hat{B}$ .

Trong một tam giác, cạnh đối diện với góc lớn hơn thì lớn hơn nên $\hat{A} < \hat{C} < \hat{B}$ thì

BC < AB < CA.

Câu 4:

Cho tam giác ABC cân ở A. Đường phân giác AD và trung tuyến CE cắt nhau tại H. Đường thẳng BH

A. chứa phân giác trong đỉnh B.

B. chứa đường cao kẻ từ B.

C. chứa trung tuyến kẻ từ B.

D. cả ba đáp án A, B và C đều đúng.

Xem đáp án

Đáp án đúng là: C

$Δ A B C$ cân ở A có AD là đường phân giác nên AD vừa là đường phân giác, vừa là đường trung tuyến của $Δ A B C$ .

$Δ A B C$ có hai đường trung tuyến AD và CE cắt nhau tại H nên H là trọng tâm $Δ A B C$ .

Do đó BH chứa trung tuyến kẻ từ đỉnh B.

Câu 5:

Cho hai đa thức:

P(x) = x⁴ + 3x³ - x + $\frac{1}{2}$ - x³ - 4x; Q(x) = $\frac{3}{2}$ - 4x³ + x⁴ - 2x - 3x + 2x³.

a) Thu gọn và sắp xếp các đa thức P(x), Q(x) theo lũy thừa giảm dần của biến;

b) Tính P(x) + Q(x); P(x) - Q(x).

Xem đáp án

P(x) = x⁴ + 3x³ - x + $\frac{1}{2}$ - x³ - 4x; Q(x) = $\frac{3}{2}$ - 4x³ + x⁴ - 2x - 3x + 2x³.

a) P(x) = x⁴ + 3x³ - x + $\frac{1}{2}$ - x³ - 4x

P(x) = x⁴ + (3x³- x³) + (-x - 4x) + $\frac{1}{2}$

P(x) = x⁴ + 2x³ - 5x + $\frac{1}{2}$

Q(x) = $\frac{3}{2}$ - 4x³ + x⁴ - 2x - 3x + 2x³

Q(x) = x⁴+ (-4x³ + 2x³) + (-2x - 3x) + $\frac{3}{2}$

Q(x) = x⁴ - 2x³ - 5x + $\frac{3}{2}$

b) P(x) + Q(x) = x⁴ + 2x³ - 5x + $\frac{1}{2}$ + x⁴ - 2x³ - 5x + $\frac{3}{2}$

P(x) + Q(x) = (x⁴ + x⁴) + (2x³ - 2x³) + (-5x - 5x) + $(\frac{1}{2} - \frac{3}{2})$

P(x) + Q(x) = 2x⁴ - 10x + 1

P(x) - Q(x) = x⁴ + 2x³ - 5x + $\frac{1}{2}$ - (x⁴ - 2x³ - 5x + $\frac{3}{2}$ )

P(x) - Q(x) = x⁴ + 2x³ - 5x + $\frac{1}{2}$ - x⁴ + 2x³ + 5x - $\frac{3}{2}$

P(x) - Q(x) = (x⁴ - x⁴) + (2x³ + 2x³) + (-5x + 5x) + $(\frac{1}{2} + \frac{3}{2})$

P(x) - Q(x) = 4x³ - 1

Câu 6:

Cho các đa thức

A(x) = 12x³ + 2ax + a²

B(x) = 2x² - $| 2 a + 3 |$ x + a²

Tìm a biết A(1) = B(-2).

Xem đáp án

A(x) = 12x³ + 2ax + a²

B(x) = 2x² - $| 2 a + 3 |$ x + a²

Với x = 1 ta có A(1) = 12.1³ + 2.a.1 + a² = 12 + 2a + a².

Với x = -2 ta có B(-2) = 2.(-2)² - $| 2 a + 3 |$ .(-2) + a² = 9 + 2 $| 2 a + 3 |$ + a².

Do A(1) = B(-2) nên 12 + 2a + a² = 9 + 2 $| 2 a + 3 |$ + a².

$\Rightarrow$ 12 + 2a + a² - 9 - a² = 2 $| 2 a + 3 |$ .

$\Rightarrow$ (12 - 9) + (a² - a²) + 2a = 2 $| 2 a + 3 |$ .

$\Rightarrow$ 3 + 2a = 2 $| 2 a + 3 |$ .

Xét 2a + 3 ≥ 0 hay a ≥ $\frac{- 3}{2}$ , khi đó $| 2 a + 3 |$ = 2a + 3.

Do đó 3 + 2a = 2(2a + 3).

$\Rightarrow$ 3 + 2a = 4a + 6

$\Rightarrow$ 2a - 4a = 6 - 3

$\Rightarrow$ -2a = 3

$\Rightarrow$ a = $\frac{- 3}{2}$ (thỏa mãn)

Xét 2a + 3 < 0 hay a < $\frac{- 3}{2}$ , khi đó $| 2 a + 3 |$ = -(2a + 3).

Do đó 3 + 2a = -2(2a + 3).

$\Rightarrow$ 3 + 2a = -4a - 6

$\Rightarrow$ 2a + 4a = -6 - 3

$\Rightarrow$ 6a = -9

$\Rightarrow$ a = $\frac{- 3}{2}$ (loại)

Vậy a= $\frac{- 3}{2}$

Câu 7:

Cho tam giác ABC cân tại A có đường cao AD.

a) Tính BC biết AB = 13 cm và AD = 12 cm.

b) Kẻ DI vuông góc với AB tại I. Lấy điểm M trên cạnh AB sao cho I là trung điểm của đoạn thẳng BM. Chứng minh DM = $\frac{1}{2}$ BC.

c) Gọi H là giao điểm của AD và CM, N là giao điểm của BH và AC. Lấy E là điểm thuộc tia đối của tia ID sao cho ID = IE. Chứng minh 3 điểm E, M, N thẳng hàng.

Xem đáp án

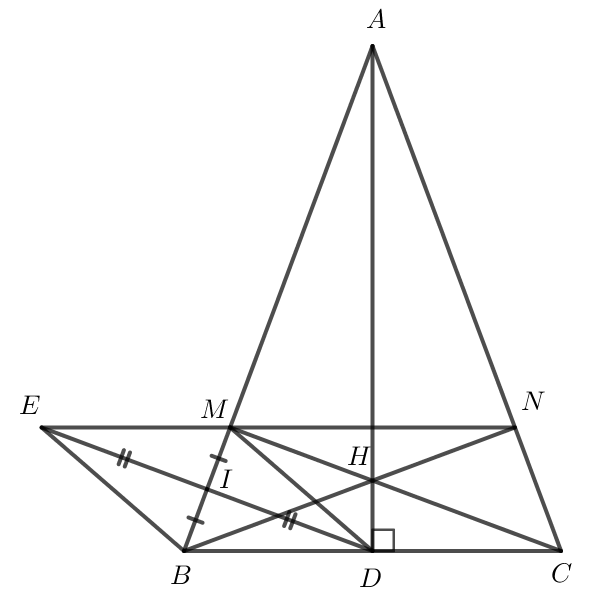
a) $Δ A B C$ cân tại A có AD là đường cao nên AD cũng là đường trung tuyến.

Do đó D là trung điểm của BC.

Áp dụng định lý Pytago vào $Δ A B D$ vuông tại D ta có:

AD² + BD² = AB²

$\Rightarrow$ 12² + BD² = 13²

$\Rightarrow$ BD²= 169 - 144

$\Rightarrow$ BD² = 25

$\Rightarrow$ BD = 5 cm.

Do D là trung điểm của BC nên BD = $\frac{1}{2}$ BC.

Do đó BC = 10 cm.

b) Xét $Δ D I M$ vuông tại I và $Δ D I B$ vuông tại I có:

ID chung.

IM = IB (theo giả thiết).

$\Rightarrow Δ D I M = Δ D I B$ (2 cạnh góc vuông).

$\Rightarrow$ DM = DB (2 cạnh tương ứng).

Mà DB = $\frac{1}{2}$ BC nên DM = $\frac{1}{2}$ BC.

c) Tam giác DIM có MD = DB = DC = $\frac{1}{2}$ BC nên Tam giác MBC vuông tại M

Do đó CM vuông góc với AB

Tam giác ABC có AD vuông góc BC, CM vuông góc AB.

Mà AD cắt CM tại H nên H là trực tâm của tam giác ABC.

Do đó: BH vuống góc AC hay BN vuông góc AC.

Do tam giác ABC cân tại A nên AB = AC và góc ABC bằng góc ACB.

Xét tam giác ANB vuông tại N và tam giác AMC vuông tại M:

Góc A chung.

AB = AC (chứng minh trên).

Tam giác ANB= tam giác AMC (cạnh huyền - góc nhọn).

Suy ra AN = AM (2 cạnh tương ứng).

tam giác AMN có AN = AM nên tam giác AMN cân tại A.

Do đó Góc AMN= góc ANM. $\hat{A M N} + \hat{A N M} + \hat{M A N} = 180 °$

Xét Tam giác AMN có

$\Rightarrow 2 \hat{A M N} + \hat{M A N} = 180 °$

$\Rightarrow \hat{A M N} = \frac{180 ° - \hat{M A N}}{2}$ (1).

Xét tam giác ABC có $\hat{A B C} + \hat{A C B} + \hat{B A C} = 180 °$

$\Rightarrow 2 \hat{A B C} + \hat{B A C} = 180 °$

$\Rightarrow \hat{A B C} = \frac{180 ° - \hat{B A C}}{2}$ (2).

Từ (1) và (2) suy ra $\hat{A M N} = \hat{A B C}$ .

Mà hai góc này ở vị trí đồng vị nên MN // BC (3).

Xét tam giác EIM và tam giác DIB có:

EI = DI (theo giả thiết).

Góc EIM =góc DIB (2 góc đối đỉnh).

IM = IB (theo giả thiết).

tam giác EIM= tam giác DIB (c - g - c).

$\Rightarrow \hat{E M I} = \hat{D B I}$ (2 góc tương ứng).

Mà hai góc này ở vị trí so le trong nên EM // BD hay EM // BC (4).

Từ (3) và (4) suy ra E, M, N thẳng hàng.

Vậy E, M, N thẳng hàng.

Câu 8:

Tìm tất cả các số nguyên dương x, y thỏa mãn:

$\frac{9}{x y} - \frac{1}{y} = 2 + \frac{3}{x}$ .

Xem đáp án

$\frac{9}{x y} - \frac{1}{y} = 2 + \frac{3}{x}$

$\Rightarrow \frac{9}{x y} - \frac{x}{x y} = \frac{2 x y}{x y} + \frac{3 y}{x y}$

Khử mẫu ta được: 9 - x = 2xy + 3y

$\Rightarrow$ 9 = x + 2xy + 3y

$\Rightarrow$ 9 = x(1 + 2y) + $\frac{3}{2}$ .2y

$\Rightarrow$ 9 + $\frac{3}{2}$ = x(1 + 2y) + $\frac{3}{2}$ .2y + $\frac{3}{2}$

$\Rightarrow$ $\frac{18}{2} + \frac{3}{2}$ = x(1 + 2y) + $\frac{3}{2}$ .(2y + 1)

$\Rightarrow$ $\frac{21}{2}$ = (1 + 2y)(x + $\frac{3}{2}$ )

$\Rightarrow$ 21 = (1 + 2y)(2x + 3)

Do x và y các số nguyên dương nên x ≥ 1; y ≥ 1.

Khi đó 2x + 3 ≥ 5; 2y + 1 ≥ 3.

Mà 21 = (1 + 2y)(2x + 3) nên 2x + 3 = 7; 2y + 1 = 3.

+) 2x + 3 = 7

$\Rightarrow$ 2x = 4

$\Rightarrow$ x = 2

+) 2y + 1 = 3

$\Rightarrow$ 2y = 2

$\Rightarrow$ y = 1

Vậy x = 2; y = 1.

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đề kiểm tra học kì 2 Toán 7 có đáp án ( Mới nhất)

Đề kiểm tra học kì 2 Toán 7 có đáp án ( Mới nhất)_ đề số 6

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương