Trắc nghiệm Toán 10 Bài 1. Bất phương trình bậc nhất hai ẩn có đáp án
-
1522 lượt thi
-
15 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Trong các bất phương trình sau đây, đâu là bất phương trình bậc nhất hai ẩn?
Hướng dẫn giải
Đáp án đúng là: B
Câu A: 4x + 5y – t + 1 > 0 là bất phương trình bậc nhất 3 ẩn x, y, t, không là bất phương trình bậc nhất hai ẩn.
Câu B: 2x – y – 1 > 0 là bất phương trình bậc nhất hai ẩn có dạng ax + by + c > 0, a = 2, b = -1, c = -1.
Câu C: x2 + y < 1 là bất phương trình có chứa x2 nên không là bất phương trình bậc nhất hai ẩn.
Câu D: - x > 0 không là bất phương trình bậc nhất hai ẩn vì không có dạng ax + by + c > 0.
Vậy ta chọn phương án B.
Câu 2:
Xác định các hệ số a, b, c của bất phương trình bậc nhất hai ẩn sau: 5x – 1 ≤ 6y?
Hướng dẫn giải
Đáp án đúng là: B
Bất phương trình 5x – 1 ≤ 6y ⇔ 5x – 6y – 1 ≤ 0 là bất phương trình bậc nhất hai ẩn dạng ax + by + c ≤ 0 nên có hệ số là a = 5, b = -6, c = -1.
Vậy ta chọn phương án B.
Câu 3:
Cặp nghiệm nào sau đây là nghiệm của bất phương trình bậc nhất hai ẩn: x + 2y – 1 < 0?
Hướng dẫn giải
Đáp án đúng là: D
+) Xét cặp số (2; 3): Thay x = 2, y = 3 vào bất phương trình ta có: 2 + 2. 3 – 1 = 7 < 0 là mệnh đề sai, nên cặp số (2; 3) không là nghiệm của bất phương trình đã cho.
+) Xét cặp số (1; 2): Thay x = 1, y = 2 vào bất phương trình ta có: 1 + 2. 2 – 1 = 4 < 0 là mệnh đề sai, nên cặp số (1; 2) không là nghiệm của bất phương trình đã cho.
+) Xét cặp số (0; 1): Thay x = 0, y = 1 vào bất phương trình ta có: 0 + 2. 1 – 1 =1 < 0 là mệnh đề sai, nên cặp số (0; 1) không là nghiệm của bất phương trình đã cho.
+) Xét cặp số (-1; 0): Thay x = -1, y = 0 vào bất phương trình ta có: -1 + 2. 0 – 1 = -2 < 0 là mệnh đề đúng, nên cặp số (-1; 0) là nghiệm của bất phương trình đã cho.
Vậy ta chọn phương án D.
Câu 4:
Điền vào chỗ trống từ còn thiếu: “Trong mặt phẳng tọa độ Oxy, tập hợp các điểm (x0; y0) sao cho ax0 + by0 + c < 0 được gọi là ……của bất phương trình ax + by + c < 0”.
Hướng dẫn giải
Đáp án đúng là: C
Trong mặt phẳng tọa độ Oxy, tập hợp các điểm (x0; y0) sao cho ax0 + by0 + c < 0 được gọi là miền nghiệm của bất phương trình ax + by + c < 0.
Câu 5:
Để biểu diễn miền nghiệm của bất phương trình bậc nhất hai ẩn 2x + y – 4 > 0, bạn An đã làm theo 3 bước:
Bước 1: Trên mặt phẳng tọa độ Oxy, vẽ đường thẳng ∆: 2x + y – 4 = 0.
Bước 2: Lấy một điểm (0; 0) không thuộc ∆. Tính 2. 0 + 0 – 4 = ‒ 4.
Bước 3: Kết luận:
Do ‒4 < 0 nên miền nghiệm của bất phương trình đã cho là nửa mặt phẳng (không kể bờ ∆) chứa điểm (0; 0).
Bước 4: Biểu diễn miền nghiệm trên trục tọa độ Oxy:

Cô giáo kiểm tra bài bạn An và nói rằng bài bạn làm sai. Bạn An đã làm sai từ bước nào?
Hướng dẫn giải
Đáp án đúng là: C
Bạn An đã làm sai ở Bước 3: Kết luận:
Do ‒4 < 0 nên miền nghiệm của bất phương trình 2x + y – 4 > 0 là nửa mặt phẳng (không kể bờ ∆) không chứa điểm (0; 0).
Câu 6:
Hình vẽ sau biểu diễn miền nghiệm (phần không bị gạch) của bất phương trình bậc nhất hai ẩn nào?
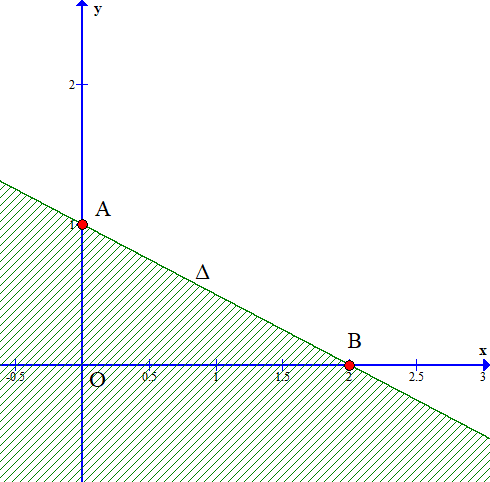
Hướng dẫn giải
Đáp án đúng là: A
Ta thấy đường thẳng ∆ cắt 2 trục tọa độ tại điểm A(0; 1) và B(2; 0).
Câu A: Thay x = 0, y = 1 vào phương trình x + 2y – 2 = 0 ta được 0 + 2. 1 – 2 = 0 = 0 là mệnh đề đúng.
Thay x = 2, y = 0 vào phương trình x + 2y – 2 = 0 ta được 2 + 2.0 – 2 = 0 = 0 là mệnh đề đúng.
Thay x = 0, y = 0 vào bất phương trình x + 2y – 2 > 0 ta được 0 + 2.0 – 2 = -2 > 0 là mệnh đề sai, vậy điểm O(0; 0) không thỏa mãn bất phương trình, nên miền nghiệm của bất phương trình x + 2y – 2 > 0 là bờ đường thẳng x + 2y – 2 = 0, không chứa điểm O. Vậy A đúng.
Câu B: Thay x = 0, y = 1 vào phương trình 3x + y – 2 = 0 ta có 3. 0 + 1 – 2 = -1 = 0 là mệnh đề sai, vậy câu B sai.
Câu C: Thay x = 0, y = 1 vào phương trình x - 2y + 1 = 0 ta có 0 - 2. 1 + 1 = -1 = 0 là mệnh đề sai, vậy câu C sai.
Câu D: Thay x = 0, y = 1 vào phương trình x + 3y = 0 ta có 0 + 3. 1 = 3 = 0 là mệnh đề sai, vậy câu D sai.
Vậy ta chọn phương án A.
Câu 7:
Chỉ ra câu sai trong các câu sau:
Hướng dẫn giải
Đáp án đúng là: C
Bất phương trình bậc nhất hai ẩn luôn có vô số nghiệm nên câu A và câu D đúng.
Thay x = 2, y = 3 vào bất phương trình 2x + 3y > 0 ta có 2. 2 + 3. 3 = 13 > 0 là mệnh đề đúng, vậy câu B đúng.
Bất phương trình 2x + 5y < 1 Û 2x + 5y – 1 < 0 là bất phương trình bậc nhất hai ẩn có hệ số là a = 2; b = 5 và c = - 1. Vậy câu C sai.
Câu 8:
Cho bất phương trình 2x + 3y – 1 ≤ 0 (1). Chọn khẳng định đúng trong các khẳng định sau:
Hướng dẫn giải
Đáp án đúng là: C
Xét cặp số (x; y) = (1; 1): Thay x = 1, y = 1 vào bất phương trình (1): 2x + 3y – 1 ≤ 0 ta được 2.1 + 3.1 – 1 = 4 > 0 là mệnh đề sai, do đó câu D là sai.
Trên mặt phẳng toạ độ, đường thẳng d: 2x + 3y – 1 = 0 chia mặt phẳng thành hai nửa mặt phẳng.
Xét điểm O(0; 0) không thuộc đường thẳng d. Ta thấy cặp số (0; 0) là nghiệm của bất phương trình x + 3y – 1 ≤ 0.
Vậy miền nghiệm của bất phương trình là nửa mặt phẳng bờ d (kể cả bờ d) chứa điểm O.
Do đó bất phương trình bậc nhất hai ẩn x + 3y – 1 ≤ 0 có vô số nghiệm, vậy câu C đúng.
Vậy ta chọn phương án C.
Câu 9:
Điểm nào sau đây thuộc miền nghiệm của bất phương trình bậc nhất hai ẩn x + 3y – 3 ≤ 0 trên mặt phẳng tọa độ Oxy?
Hướng dẫn giải
Đáp án đúng là: C
Thay x = 4; y = 5 vào bất phương trình đã cho ta có 4 + 3. 5 – 3 = 16 ≤ 0 là mệnh đề sai, vậy A không thuộc miền nghiệm bất phương trình đã cho.
Thay x = 2; y = 3 vào bất phương trình đã cho ta có 2 + 3. 3 – 3 = 8 ≤ 0 là mệnh đề sai, vậy B không thuộc miền nghiệm bất phương trình đã cho.
Thay x = -1; y = 1 vào bất phương trình đã cho ta có -1 + 3. 1 – 3 = -1 ≤ 0 là mệnh đề đúng, vậy C thuộc miền nghiệm bất phương trình đã cho.
Thay x = 4; y = 6 vào bất phương trình đã cho ta có 4 + 3. 6 – 3 = 19 ≤ 0 là mệnh đề sai, vậy D không thuộc miền nghiệm bất phương trình đã cho.
Vậy ta chọn phương án C.
Câu 10:
Hướng dẫn giải
Đáp án đúng là: B
Thay x = 0; y = 0 vào bất phương trình 3x + 4y – 1 > 0 ta có: 3. 0 + 4. 0 – 1 = -1 > 0 là mệnh đề sai, vậy điểm O(0; 0) không thuộc miền nghiệm của bất phương trình 3x + 4y – 1 > 0. Do đó A là sai.
Thay x = 0; y = 0 vào bất phương trình 2x + 3y – 2 < 0 ta có: 2. 0 + 3. 0 – 2 = -2 < 0 là mệnh đề đúng, vậy điểm O(0; 0) thuộc miền nghiệm của bất phương trình 2x + 3y – 2 < 0. Do đó B là đúng.
Thay x = 0; y = 0 vào bất phương trình x – y > 1 ta có: 0 - 0 = 0 > 1 là mệnh đề sai, vậy điểm O(0; 0) không thuộc miền nghiệm của bất phương trình x – y > 1. Do đó C là sai.
Thay x = 0; y = 0 vào bất phương trình x + 3y -1 > 0 ta có: 0 + 3. 0 – 1 = -1 > 0 là mệnh đề sai, vậy điểm O(0; 0) không thuộc miền nghiệm của bất phương trình x + 3y -1 > 0. Do đó D là sai.
Vậy ta chọn phương án B.
Câu 11:
Miền nghiệm của bất phương trình x + y ≤ 2 là phần tô đậm trong hình vẽ của hình vẽ nào, trong các hình vẽ sau?
Hướng dẫn giải
Đáp án đúng là: A
Xét đường thẳng x + y – 2 = 0 là đường thẳng đi qua hai điểm A(2; 0) và B(0; 2). Do đó ta loại phương án C và D.
Thay x = 0 và y = 0 vào bất phương trình ta có 0 + 0 = 0 ≤ 2 là mệnh đề đúng, vậy O(0; 0) thuộc miền nghiệm của bất phương trình đã cho.
Do vậy miền nghiệm của bất phương trình x + y ≤ 2 là nửa mặt phẳng (kể cả bờ là đường thẳng x + y = 2) và chứa điểm O(0; 0) (phần tô đậm).
Theo hình vẽ ta chọn phương án A.
Câu 12:
Cho các khẳng định sau:
(I) 2x + y - 1 = 0 là bất phương trình bậc nhất hai ẩn.
(II) Bất phương trình bậc nhất hai ẩn luôn có vô số nghiệm.
(III) Điểm A(0; 1) thuộc miền nghiệm của bất phương trình x + 2y – 1 > 0.
(IV) Cặp số (x; y) = (3; 4) là nghiệm của bất phương trình x + y > 0.
Hỏi có bao nhiêu khẳng định đúng?
Hướng dẫn giải
Đáp án đúng là: C
Xét câu (I): 2x + y - 1 = 0 là phương trình bậc nhất hai ẩn, do đó câu (I) sai.
Xét câu (II): Bất phương trình bậc nhất hai ẩn luôn có vô số nghiệm, do đó câu (II) đúng.
Xét câu (III): Thay x = 0, y = 1 vào bất phương trình x + 2y – 1 > 0 ta có 0 + 2. 1 – 1 = 1 > 0 là mệnh đề đúng, vậy điểm A(0; 1) thuộc miền nghiệm của bất phương trình x + 2y – 1 > 0, do đó câu (III) đúng.
Xét câu (IV): Thay x = 3, y = 4 vào bất phương trình x + y > 0 ta có 3 + 4 = 7 > 0 là mệnh đề đúng, vậy cặp (x; y) = (3; 4) là nghiệm của bất phương trình x + y > 0, do đó câu (IV) đúng.
Vậy có 3 câu đúng, ta chọn phương án C.
Câu 13:
Miền nghiệm của bất phương trình 2(x + 1) – 3(y + 2) > 3(2x + 2y) được biểu diễn phân cách bởi đường thẳng nào sau đây?
Hướng dẫn giải
Đáp án đúng là: A
Bất phương trình: 2(x + 1) – 3(y + 2) > 3(2x + 2y)
⇔ 2x + 2 – 3y – 6 > 6x + 6y
⇔ 6x + 6y < 2x – 3y – 4
⇔ 6x + 6y – 2x + 3y + 4 < 0
⇔ 4x + 9y + 4 < 0.
Vậy miền nghiệm của bất phương trình 2(x + 1) – 3(y + 2) > 3(2x + 2y) được biểu diễn phân cách bởi đường thẳng 4x + 9y + 4 = 0.
Câu 14:
Cặp số (2; 3) không là nghiệm của bất phương trình nào sau đây?
Hướng dẫn giải
Đáp án đúng là: A
Thay x = 2, y = 3 vào bất phương trình x + y < 0 ta có 2 + 3 = 5 < 0 là mệnh đề sai, vậy cặp số (2; 3) không là nghiệm của bất phương trình x + y < 0. Do đó A là đúng.
Thay x = 2, y = 3 vào bất phương trình x + y > 0 ta có 2 + 3 = 5 > 0 là mệnh đề đúng, vậy cặp số (2; 3) là nghiệm của bất phương trình x + y > 0. Do đó B là sai.
Thay x = 2, y = 3 vào bất phương trình x - y < 0 ta có 2 - 3 = -1 < 0 là mệnh đề đúng, vậy cặp số (2; 3) là nghiệm của bất phương trình x - y < 0. Do đó C là sai.
Thay x = 2, y = 3 vào bất phương trình 2x - y > 0 ta có 2. 2 - 3 = 1 > 0 là mệnh đề đúng, vậy cặp số (2; 3) là nghiệm của bất phương trình 2x - y > 0. Do đó D là sai.
Vậy ta chọn phương án A.
Câu 15:
Khi x = 2 và y ≥ 0 thì bất phương trình sau có mấy cặp nghiệm nguyên: 2x + y < 6?
Hướng dẫn giải
Đáp án đúng là: C
Khi x = 2 thay vào bất phương trình ta có: 2. 2 + y < 6 ⇔ y < 2.
Mà y ≥ 0 và y là số nguyên nên y ∈ {0; 1}.
Vậy bất phương trình có 2 cặp nghiệm nguyên là (x; y) ∈ {(2; 0); (2; 1)}.
