Trắc nghiệm Toán 10 Bài tập cuối chương 4 có đáp án
-
463 lượt thi
-
30 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Giá trị của biểu thức M = tan1°.tan2°.tan3°….tan89° là:
Hướng dẫn giải
Đáp án đúng là: C
Ta có:
tan89° = tan(90° ‒ 1°) = cot1°;
tan88° = tan(90° ‒ 2°) = cot2°;
…
tan46° = tan(90° ‒ 44°) = cot44°.
Do đó: M = tan1°.tan2°.tan3°….tan89°
M = tan1°.tan2°….tan44°.tan45°.cot44°….cot2°.cot1°
M = (tan1°.cot1°).(tan2°.cot2°)…(tan44°.cot44°).tan45°
M = 1.1….1.1
M = 1.
Vậy M = 1.
Câu 3:
Cho tam giác ABC có AB = 8, AC = 9, BC = 10. Tam giác ABC là tam giác:
Hướng dẫn giải
Đáp án đúng là: A
Áp dụng hệ quả định lí côsin trong tam giác ABC ta có:
Suy ra là góc nhọn.
Tam giác ABC có cạnh BC lớn nhất đối diện với nên là góc lớn nhất.
Do đó cũng là góc nhọn.
Vậy tam giác ABC là tam giác nhọn.
Câu 4:
Tam giác ABC có các góc Tỉ số bằng:
Hướng dẫn giải
Đáp án đúng là: C
Xét tam giác ABC có ta có:
(định lí tổng ba góc trong tam giác)
Áp dụng định lí sin trong tam giác ABC ta có:
Vậy
Câu 5:
Tam giác ABC có với BC = a, AC = b, AB = c thì câu nào sau đây là đúng?
Hướng dẫn giải
Đáp án đúng là: C
Áp dụng định lí côsin trong tam giác ABC ta có:
a2 = b2 + c2 ‒ 2.bc.cosA
Þ a2 = b2 + c2 ‒ 2.bc.cos120°
Þ a2 = b2 + c2 + bc.
Vậy a2 = b2 + c2 + bc.
Câu 6:
Cho hình thoi ABCD cạnh bằng 1 cm và có . Độ dài cạnh AC là:
Hướng dẫn giải
Đáp án đúng là: A
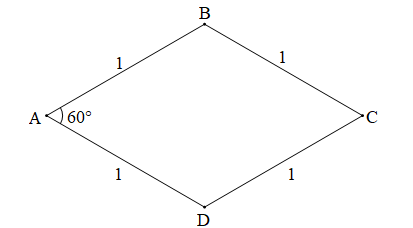
Vì ABCD là hình thoi nên BC // AD (tính chất hình thoi)
Do đó (hai góc trong cùng phía)
Mà
Áp dụng định lí côsin cho tam giác ABC ta có:
AC2 = AB2 + BC2 – 2.AB.BC.
Þ AC2 = 12 + 12 – 2.1.1.cos120° = 3
Vậy
Câu 7:
Tam giác ABC có . Gọi D là chân đường phân giác trong góc A. Khi đó số đo của góc ADB là:
Hướng dẫn giải
Đáp án đúng là: C
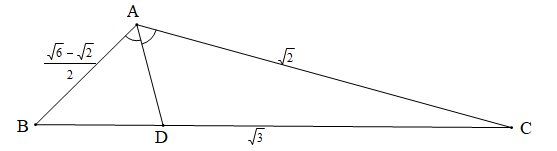
Áp dụng hệ quả định lí côsin trong tam giác ABC ta có:
+)
+)
( vì AD là tia phân giác của )
Xét tam giác ABD có và ta có:
(định lí tổng ba góc trong tam giác)
Vậy
Câu 8:
Tam giác có ba cạnh lần lượt là và 1. Độ dài đường cao ứng với cạnh lớn nhất là:
Hướng dẫn giải
Đáp án đúng là: D
Nửa chu vi tam giác là:
Diện tích tam giác theo công thức Heron là:
(đơn vị diện tích)
Mặt khác
Do đó đường cao ứng với cạnh lớn nhất là:
Vậy độ dài đường cao ứng với cạnh lớn nhất của tam giác là
Câu 9:
Tam giác ABC có góc B tù, AB = 3, AC = 4 và có diện tích bằng . Số đo góc A là:
Hướng dẫn giải
Đáp án đúng là: C
Tam giác ABC có góc B tù nên suy ra góc A là góc nhọn.
Diện tích tam giác ABC là:
Mà góc A là góc nhọn
Câu 10:
Tam giác ABC vuông cân tại A và nội tiếp trong đường tròn tâm O, bán kính R. Gọi r là bán kính đường tròn nội tiếp tam giác ABC. Tỉ số là:
Hướng dẫn giải
Đáp án đúng là: A
Xét tam giác ABC vuông cân tại A, giả sử AB = AC = a, theo định lí Py – ta – go ta có:
BC2 = AB2 + AC2 = a2 + a2 = 2a2
Do đó nửa chu vi tam giác ABC là
Tam giác ABC vuông tại A nên diện tích tam giác ABC là:
Mặt khác
và
Do đó
Vậy
Câu 11:
Cho hình chữ nhật ABCD có AB = 4, BC = 6. M là trung điểm của BC, N là điểm trên cạnh CD sao cho ND = 3NC. Khi đó bán kính của đường tròn ngoại tiếp tam giác AMN bằng:
Hướng dẫn giải
Đáp án đúng là: D
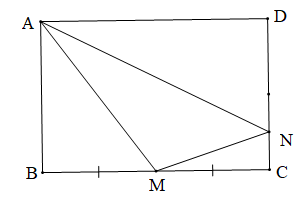
Vì M là trung điểm của BC nên BM = MC = 3.
Vì ND = 3NC nên NC = 1 và ND = 3.
Tam giác CMN vuông tại C theo định lí Py – ta – go có:
MN2 = MC2 + NC2 = 32 + 12 = 10
Tam giác AND vuông tại D theo định lí Py – ta – go có:
AN2 = AD2 + DN2 = 62 + 32 = 45
Tam giác ABM vuông tại B theo định lí Py – ta – go ta có:
AM2 = AB2 + BM2 = 42 + 32 = 25 Þ AM = 5.
Nửa chu vi của tam giác AMN là:
Diện tích tam giác AMN theo công thức Heron là:
(đơn vị diện tích)
Mặt khác
Vậy bán kính đường tròn ngoại tiếp tam giác AMN bằng
Câu 12:
Một tam giác có ba cạnh là 52, 56, 60. Gọi R, r lần lượt là bán kính đường tròn ngoại tiếp, nội tiếp tam giác. Khi đó R. r bằng:
Hướng dẫn giải
Đáp án đúng là: B
Giả sử tam giác có độ dài ba cạnh là a = 52, b = 56, c = 60.
Nửa chu vi tam giác là:
Ta có diện tích tam giác là:
Þ 52.56.60 = 84r.4R
Þ R.r = 520.
Vậy R.r = 520.
Câu 13:
Cho tam giác ABC có BC = a, CA = b, AB = c. Mệnh đề nào sau đây là đúng?
Hướng dẫn giải
Đáp án đúng là: C
Áp dụng định lí côsin trong tam giác ABC ta có: c2 = a2 + b2 – 2.a.b.cosC
Þ a2 + b2 ‒ c2 = 2.a.b.cosC
+) Nếu a2 + b2 – c2 < 0 thì 2.a.b.cosC < 0 nên cosC < 0 Þ là góc tù;
+) Nếu a2 + b2 – c2 > 0 thì 2.a.b.cosC > 0 nên cosC > 0 Þ là góc nhọn.
Vậy ta chọn phương án C.
Câu 14:
Cho tam giác ABC đều, ABC có độ dài cạnh bằng 1. Dựng ra phía ngoài tam giác các hình vuông ABDE, BCMN, CAHK. Diện tích lục giác DEHKMN bằng:
Hướng dẫn giải
Đáp án đúng là: C

- Tam giác ABC là tam giác đều nên
Diện tích tam giác ABC là:
(đơn vị diện tích).
- Hình vuông ABDE có cạnh AB = 1 nên có diện tích là: SABDE = 12 = 1 (đơn vị diện tích).
Tương tự SBCMN = 1 (đơn vị diện tích) và SCAHK = 1 (đơn vị diện tích).
- Tam giác AEH có:
Diện tích tam giác AEH là:
(đơn vị diện tích).
Tương tự ta có: (đơn vị diện tích) và (đơn vị diện tích)
Do đó diện tích của lục giác DEHKMN là:
SDEHKMN = SABC + 3.SABDE + 3.SAEH
(đơn vị diện tích).
Vậy (đơn vị diện tích).
Câu 15:
Cho tam giác ABC. Khẳng định nào sau đây là sai?
Hướng dẫn giải
Đáp án đúng là:
Áp dụng hệ quả định lí sin cho tam giác ABC ta có:
BC = 2R.sinA; AC = 2R.sinB; AB = 2R.sinC.
Theo bất đẳng thức trong tam giác ta có: AB + AC > BC
Þ 2R.sinC + 2R.sinB > 2R.sinA
Þ sinC + sinB > sinA.
Chứng minh tương tự ta cũng có: sinA + sinB > sinC và sinA + sinC > sinB.
Do đó phương án D là sai.
Vậy ta chọn phương án D.
Câu 16:
Cho tam giác ABC. Giá trị biểu thức sinA.cos(B + C) + cosA.sin(B + C) là:
Hướng dẫn giải
Đáp án đúng là: B
Xét tam giác ABC ta có: (định lí tổng ba góc trong tam giác)
Þ cos(B + C) = cos(180° ‒ A) = ‒cosA;
Và sin(B + C) = sin(180° ‒ A)= sinA.
Do đó:
sinA.cos(B + C) + cosA.sin(B + C)
= sinA.(‒cosA) + cosA.sinA
= ‒sinA.cosA + cosA.sinA
= 0
Vậy sinA.cos(B + C) + cosA.sin(B + C) = 0.
Câu 17:
Trong các đẳng thức sau, đẳng thức nào sai?
Hướng dẫn giải
Đáp án đúng là: A
Ta có:
+) sin0° + cos0° = 0 + 1 = 1. Do đó phương án A là mệnh đề sai.
+) sin90° + cos90° = 1 + 0 = 1. Do đó phương án B là mệnh đề đúng.
+) sin180° + cos180° = 0 + (‒1) = ‒1. Do đó phương án C là mệnh đề đúng.
+) Do đó phương án D là mệnh đề đúng.
Vậy ta chọn phương án A.
Câu 18:
Cho góc α (0° ≤ α ≤ 180°) với tanα = ‒3. Giá trị của bằng bao nhiêu?
Hướng dẫn giải
Đáp án đúng là: D
Vì tanα = ‒3 nên do đó cosα ≠ 0
Ta có:
(do cosα ≠ 0)
Vậy
Câu 19:
Cho góc α (0° ≤ α ≤ 180°). Trong các khẳng định sau, khẳng định nào sai?
Hướng dẫn giải
Đáp án đúng là: D
Với mỗi góc α (0° ≤ α ≤ 180°) ta xác định được một điểm M duy nhất trên nửa đường tròn đơn vị sao cho ![]() . Gọi (x0; y0) là toạ độ điểm M, ta có:
. Gọi (x0; y0) là toạ độ điểm M, ta có:
- Tung độ y0 của M là sin của góc α, kí hiệu là sinα = y0;
- Hoành độ x0 của M là côsin của góc α, kí hiệu là cosα = x0;
- Tỉ số (x0 ≠ 0) là tang của góc α, kí hiệu là
- Tỉ số (y0 ≠ 0) là côtang của góc α, kí hiệu là
Gọi H và K lần lượt là hình chiếu của M lên Ox và Oy.
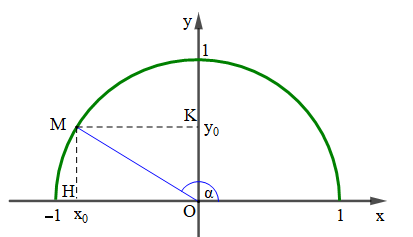
Khi đó ta có: OH = x0 = cosα, MH = OK = y0 = sinα, OM = 1.
Tam giác OMH vuông tại H, áp dụng định lí Pythagore ta có:
MH2 + OH2 = OM2
Hay sin2α + cos2α = 1.
Do đó phương án A là mệnh đề đúng.
Với 0° < α < 180° và α ≠ 90° ta có:
Do đó phương án B là mệnh đề đúng.
Với α ≠ 90° ta có: (do sin2α + cos2α = 1).
Do đó phương án C là mệnh đề đúng.
Với 0° < α < 180° và α ≠ 90° ta có:
(do sin2α + cos2α = 1).
Do đó phương án D là mệnh đề sai.
Vậy ta chọn phương án D.
Câu 20:
Giá trị α (0° ≤ α ≤ 180°) thoả mãn tanα = 1,607 gần nhất với giá trị:
Hướng dẫn giải
Đáp án đúng là: C
Để tìm α khi biết tanα = 1,607 thì ta sử dụng máy tính cầm tay và tính được: α ≈ 58°.
Vậy α ≈ 58°.
Câu 21:
Cho tam giác ABC thỏa mãn: . Khi đó ABC là một tam giác:
Hướng dẫn giải
Đáp án đúng là: C
Ta có:
Þ
Þ DABC vuông tại A hoặc DABC cân tại A.
Vậy DABC vuông tại A hoặc DABC cân tại A.
Câu 22:
Cho tam giác ABC nội tiếp đường tròn bán kính R, AB = R, Tính số đo của biết là góc tù.
Hướng dẫn giải
Đáp án đúng là: A
Trong tam giác ABC có là góc tù nên là góc nhọn.
Áp dụng định lí sin trong tam giác ABC ta có:
(vì là góc nhọn)
Xét tam giác ABC có ta có:
(định lí tổng ba góc trong tam giác)
Vậy
Câu 23:
Tam giác ABC có ba cạnh lần lượt là: 2, 3, 4. Góc nhỏ nhất của tam giác có côsin bằng bao nhiêu?
Hướng dẫn giải
Đáp án đúng là: B
Góc nhỏ nhất ứng với cạnh đối diện có độ dài nhỏ nhất.
Giả sử tam giác ABC có AB = 2, AC = 3, BC = 4. Khi đó góc nhỏ nhất là góc C ứng với cạnh đối diện AB.
Áp dụng hệ quả định lí côsin trong tam giác ABC ta có:
Vậy côsin của góc nhỏ nhất trong tam giác bằng
Câu 24:
Tam giác ABC có AB = 10, AC = 24, diện tích bằng 120. Độ dài đường trung tuyến AM là:
Hướng dẫn giải
Đáp án đúng là: B
Diện tích tam giác ABC là:
Mà
Þ DABC vuông tại A
Xét tam giác ABC vuông tại A, theo định lí Py – ta – go ta có:
BC2 = AB2 + AC2 Þ BC2 = 102 + 242 = 676
Þ BC = 26.
Do đó trung tuyến AM ứng với cạnh huyền BC có độ dài là:
Vậy độ dài đường trung tuyến AM bằng 13.
Câu 25:
Tam giác ABC vuông tại A có AB = AC = 30 cm. Hai đường trung tuyến BE và CF cắt nhau tại G. Diện tích tam giác GEC là:
Hướng dẫn giải
Đáp án đúng là: C
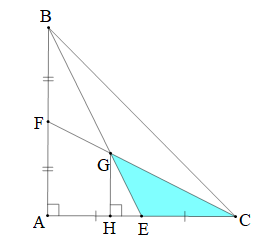
Vì BE là trung tuyến của tam giác ABC nên E là trung điểm của AC.
Do đó
Hai đường trung tuyến BE và CF cắt nhau tại G nên G là trọng tâm của tam giác ABC.
Khi đó (tính chất trọng tâm của tam giác)
Hay
Gọi H là chân đường vuông góc kẻ từ G xuống AC.
Suy ra GH // AB.
Do đó (định lí Ta – let trong tam giác ABE)
Hay
Diện tích tam giác GEC là:
Vậy diện tích tam giác GEC là 75 cm2.
Câu 26:
Tam giác ABC có BC = a, CA = b, AB = c và có diện tích S. Nếu tăng cạnh BC lên 2 lần đồng thời tăng cạnh AC lên 3 lần và giữ nguyên độ lớn của góc C thì khi đó diện tích của tam giác mới được tạo nên bằng:
Hướng dẫn giải
Đáp án đúng là: D
Ta có diện tích ban đầu của tam giác ABC là: .
Diện tích của tam giác mới sau khi thay đổi kích thước là:
.
Vậy diện tích của tam giác mới được tạo thành là 6S.
Câu 27:
Để đo chiều cao từ mặt đất đến đỉnh cột cờ của một kỳ đài trước Ngọ Môn (Đại Nội – Huế), người ta cắm hai cọc AM và BN cao 1,5 mét so với mặt đất. Hai cọc này song song và cách nhau 10 mét và thẳng hàng so với tim cột cờ (Hình vẽ minh họa). Đặt giác kế tại đỉnh A và B để nhắm đến đỉnh cột cờ, người ta được các góc lần lượt là 51°40' và 45°39' so với đường song song mặt đất.
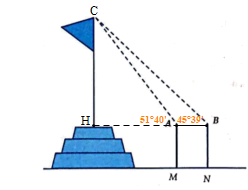
Chiều cao của cột cờ (làm tròn kết quả đến chữ số thập phân thứ hai) là:
Hướng dẫn giải
Đáp án đúng là: C
Ta có
Xét tam giác ABC ta có: (định lí tổng ba góc trong tam giác)
Áp dụng định lí sin trong tam giác ABC ta có:
Xét tam giác ACH vuông tại H có:
≈ 53,51 (m)
Chiều cao của cột cờ là khoảng: 1,5 + 53,51 = 55,01 (m)
Vậy cột cờ cao khoảng 55,01 m.
Câu 28:
Trong khi khai quật một ngôi mộ cổ, các nhà khảo cổ học đã tìm được một chiếc đĩa cổ hình tròn bị vỡ, các nhà khảo cổ muốn khôi phục hình dạng chiếc đĩa này. Để xác định bán kính của chiếc đĩa, các nhà khảo cổ lấy 3 điểm trên chiếc đĩa và tiến hành đo đạc thu được kết quả như hình vẽ (AB = 4,3 cm; BC = 3,7 cm; CA = 7,5 cm).
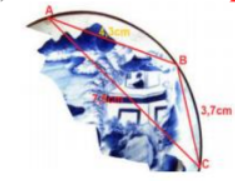
Bán kính của chiếc đĩa này bằng (kết quả làm tròn đến chữ số thập phân thứ hai):
Hướng dẫn giải
Đáp án đúng là: A
Bán kính R của chiếc đĩa bằng bán kính đường tròn ngoại tiếp tam giác ABC.
Nửa chu vi của tam giác ABC là:
Diện tích tam giác ABC theo công thức Heron là:
Mặt khác:
Vậy bán kính của chiếc đĩa là khoảng 5,73 cm.
Câu 29:
Vào lúc 9 giờ sáng, hai vận động viên A và B xuất phát từ cùng một vị trí O. Vận động viên A chạy với vận tốc 13 km/h theo một góc so với hướng Bắc là 15°, vận động viên B chạy với vận tốc 12 km/h theo một góc so với hướng Bắc là 135° (hình vẽ).
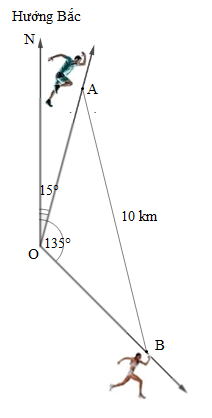
Tại thời điểm nào thì vận động viên A cách vận động viên B một khoảng 10 km (làm tròn kết quả đến phút)?
Hướng dẫn giải
Đáp án đúng là: B
Gọi x giờ (x > 0) là khoảng thời gian kể từ khi bắt đầu chạy từ điểm O đến khi hai vận động viên cách nhau 10 km.
Khi đó đoạn đường mà vận động viên A chạy được là 13x (km);
Đoạn đường mà vận động viên B chạy được là 12x (km).
Theo hình vẽ trên ta có: AB = 10, OA = 13x, OB = 12x và
Áp dụng định lí côsin trong tam giác OAB ta có:
AB2 = OA2 + OB2 – 2.OA.OB.
Þ 102 = (13x)2 + (12x)2 – 2.13x.12x.sin120°
Þ x ≈ 0,483 (giờ) (vì x > 0) ≈ 29 phút.
Do đó thời điểm mà hai vận động viên cách nhau 10 km là khoảng: 9 giờ 29 phút.
Vậy vào khoảng 9 giờ 29 phút thì hai vận động viên sẽ cách nhau 10 km.
Câu 30:
Trong sơ đồ, chùm sáng S hướng vào gương màu xanh, phản xạ vào gương màu đỏ và sau đó phản xạ vào gương màu xanh như hình vẽ. Biết OP = 2 m, m.
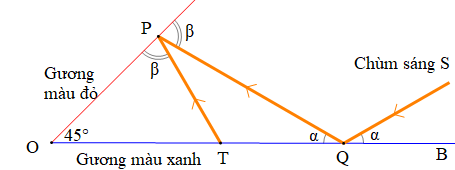
Khi đó đoạn PT bằng:
Hướng dẫn giải
Đáp án đúng là: A
Ta có:
Áp dụng định lí côsin trong tam giác OPQ ta có:
PQ2 = OP2 + OQ2 – 2.OP.OQ.cos
Þ PQ2 = 8
Áp dụng hệ quả định lí côsin trong tam giác OPQ ta có:
Þ α = 30°
Xét tam giác POQ có: β = 45° + α (tính chất góc ngoài của tam giác)
Þ β = 45° + 30° = 75°
Xét tam giác OTP ta có: (định lí tổng ba góc trong tam giác)
Hay
Áp dụng định lí sin cho tam giác OTP ta có:
Vậy
