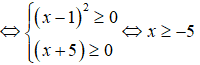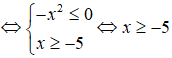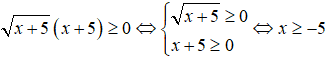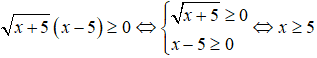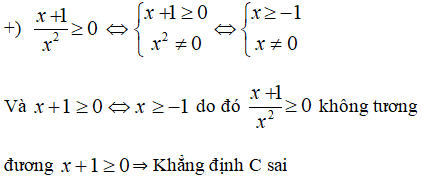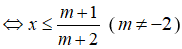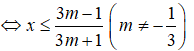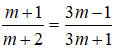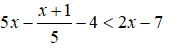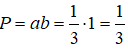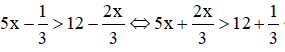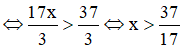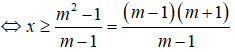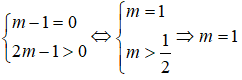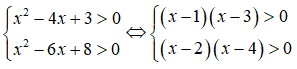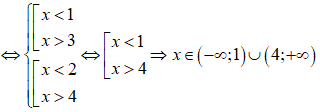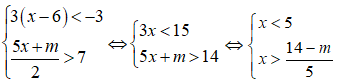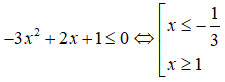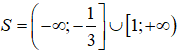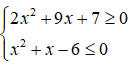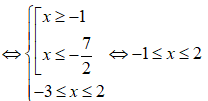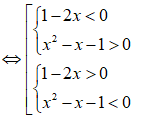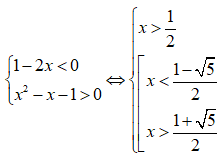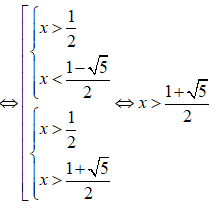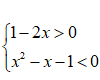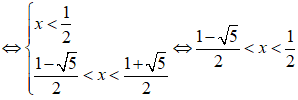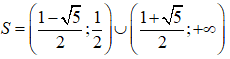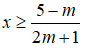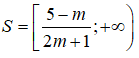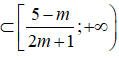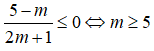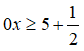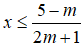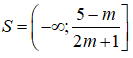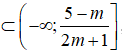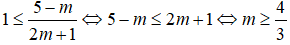Đề kiểm tra 45 phút Đại số 10 Chương 4 có đáp án (Đề 1)
-
1976 lượt thi
-
15 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Phần I: Trắc nghiệm (6 điểm)
Tập xác định của hàm số là:
Chọn D.
Hàm số xác định khi 2 - x > 0 ⇒ x < 2.
Tập xác định của hàm số là S = (;2).
Câu 2:
Bất phương trình nào sau đây không tương đương với bất phương trình x + 5 ≥ 0?
Chọn D.
+) Xét bất phương trình x + 5 ≥ 0 ⇔ x ≥ -5
⇒ Tập nghiệm của bất phương trình là S = [-5;+)
+) Xét bất phương trình (x - 1(x + 5) ≥ 0
Tập nghiệm của bất phương trình là S = [-5;).
+) Xét bất phương trình -(x + 5) ≤ 0
Tập nghiệm của bất phương trình là S = [-5;).
+) Xét bất phương trình
Tập nghiệm của bất phương trình là S = [-5;).
+) Xét bất phương trình
Tập nghiệm của bất phương trình là S = [5;).
Vậy bất phương trình
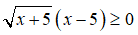
không tương đương với bất phương trình x + 5 ≥ 0.
Câu 3:
Khẳng định nào sau đây đúng?
Chọn D.
+) ≤ 3x ⇔ - 3x ≤ 0 ⇔ 0 ≤ x ≤ 3 ⇒ Khẳng định A sai
+) 
⇒ x < 0 (vì 1 > 0) ⇒ Khẳng định B sai
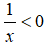
+) x + |x| ≥ x ⇔ x + |x| - x ≥ 0 ⇔ |x| ≥ 0 ⇒ Khẳng định D đúng
Câu 4:
Với giá trị nào của m thì hai bất phương trình (m + 2)x ≤ m + 1 và 3m(x - 1) ≤ -x - 1 tương đương:
Chọn D.
+) (m + 2)x ≤ m + 1 
+) 3m(x - 1) ≤ -x - 1 ⇔ 3mx - 3m + x + 1 ≤ (3m + 1)x ≤ 3m - 1
Hai bất phương trình (m + 2)x ≤ m + 1 và 3m(x - 1) ≤ -x - 1 tương đương khi và chỉ khi hai bất phương trình có cùng tập nghiệm khi đó:
⇔ (m + 1)(3m + 1) = (m + 2)(3m - 1)
⇔ 3 + m + 3m + 1 = 3 - m + 6m - 2
⇔ 3 + m + 3m + 1 - 3 + m - 6m + 2 = 0
⇔ -m + 3 = 0
⇔ m = 3 (thỏa mãn)
Câu 5:
Tập nghiệm của bất phương trình: là:
Chọn C.
⇔ 25x - (x + 1) - 20 < 10x - 35
⇔ 25x - x - 1 - 20 - 10x + 35 < 0
⇔ 14x + 14 < 0
⇔ x < -1
Vậy tập nghiệm của bất phương trình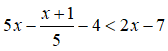 
là S = (;-1).
Câu 6:
Tập nghiệm của bất phương trình: |2x-1| ≤ x là S = [a;b]. Tính P = a.b ?
Chọn D.
Ta có:
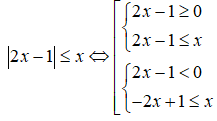
Tập nghiệm của bất phương trình là
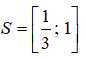
suy ra
Câu 7:
Bất phương trình mx > 3 + m vô nghiệm khi:
Chọn A.
Với m = 0, bất phương trình trở thành 0.x < 3 + 0 ⇒ 0 > 3 (vô lý)
Bất phương trình vô nghiệm khi m = 0.
Câu 8:
Số nghiệm tự nhiên nhỏ hơn 6 của bất phương trình là:
Chọn A.
Kết hợp với điều kiện x là số tự nhiên nhỏ hơn 6 ⇒ x ∈ {3; 4; 5}
Câu 9:
Cho bất phương trình: m(x - m) ≥ x - 1. Các giá trị nào sau đây của m thì tập nghiệm của bấtphương trình là S = (;m + 1]:
Chọn C.
Ta có: m(x - m) ≤ x - 1 ⇔ mx - ≥ x - 1 ⇔ (m - 1)x ≥ - 1
+) Với m < 1 ⇒ m – 1 < 0 ⇒ Tập nghiệm của bất phương trình là S = (;m+1].
+) Với m > 1 ⇒ m – 1 > 0 ⇒ Tập nghiệm của bất phương trình là S = [m+1;).
Câu 10:
Với giá trị nào của m thì bất phương trình ( + m + 1)x - 5m ≥ ( + 2)x - 3m - 1 vô nghiệm ?
Chọn A.
Bất phương trình ( + m + 1)x - 5m ≥ ( + 2)x - 3m - 1 ⇔ (m - 1)x ≥ 2m - 1 vô nghiệm khi
Câu 11:
Tập nghiệm của hệ bất phương trình là:
Chọn B.
Ta có:
Vậy tập nghiệm của bất phương trình là S = (;1) ∪ (4;).
Câu 12:
Tìm tất cả các giá trị thực của tham số m để hệ bất phương trình có nghiệm.
Chọn A.
Hệ bất phương trình có nghiệm
⇔ 14 - m < 25 ⇔ -m < 11 ⇔ m > -11
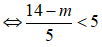
Câu 13:
Phần II: Tự luận (4 điểm)
Giải các bất phương trình và hệ bất phương trình sau:
a) -3 + 2x + 1 ≥ 0
b)
c) (1 - 2x)( - x - 1) < 0
a) Tam thức f(x) = -3 + 2x + 1 có a = -3 < 0 và có hai nghiệm x1 = -1/3; x2 = 1
Theo đề bài, f(x) < 0, a < 0 ⇒ f(x) cùng dấu với hệ số
Suy ra
Vậy tập nghiệm của bất phương trình là
b) 
Vậy tập nghiệm của hệ bất phương trình là S = [-1;2].
c) (1 - 2x)( - x - 1) < 0
Trường hợp 1:
Trường hợp 2: 
Vậy tập nghiệm của hệ bất phương trình là:
Câu 14:
Cho bất phương trình: (2m + 1)x + m - 5 ≥ 0
Tìm điều kiện của m để bất phương trình có nghiệm đúng với ∀x ∈ (0;1).
(2m + 1)x + m - 5 ≥ 0 ⇔ (2m + 1)x ≥ 5 - m (*)
TH1: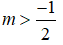 
, bất phương trình (*) trở thành: 
Tập nghiệm của bất phương trình là:
Để bất phương trình đã cho nghiệm đúng với ∀x ∈ (0;1)
thì (0;1) 
Hay 
TH2: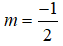 
, bất phương trình (*) trở thành: 
Bất phương trình vô nghiệm. ⇒ không có m .
TH3: Với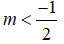 
, bất phương trình (*) trở thành: 
Tập nghiệm của bất phương trình là:
Để bất phương trình đã cho nghiệm đúng với ∀x ∈ (0;1)
thì (0;1) 
Hay 
Kết hợp điều kiện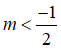 
, ⇒ không có m thỏa mãn.
Vậy với m ≥ 5, bất phương trình đã cho nghiệm đúng với ∀x ∈ (0;1).
