Trắc nghiệm Toán 10 Bài 11. Tích vô hướng của hai vecto có đáp án
-
353 lượt thi
-
16 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Trong mặt phẳng tọa độ, cặp vectơ nào sau đây vuông góc với nhau?
Đáp án đúng là D
Ta có: \(\overrightarrow a .\overrightarrow b = 1.\left( { - 1} \right) + \left( { - 1} \right).1 = - 1 + \left( { - 1} \right) = - 2 \ne 0.\) Suy ra hai vecto \(\overrightarrow a ,\overrightarrow b \) không vuông góc với nhau. Do đó A sai.
Ta có: \(\overrightarrow n .\overrightarrow k = 1.2 + 1.0 = 2 + 0 = 2 \ne 0.\) Suy ra hai vecto \(\overrightarrow n ,\overrightarrow k \) không vuông góc. Do đó B sai.
Ta có: \(\overrightarrow u .\overrightarrow v = 2.4 + 3.6 = 8 + 18 = 26 \ne 0.\) Suy ra hai vecto \(\overrightarrow u ,\overrightarrow v \) không vuông góc. Do đó C sai.
Ta có: \(\overrightarrow z .\overrightarrow t = a.\left( { - b} \right) + b.a = - ab + ab = 0.\) Suy ra hai vecto \(\overrightarrow z ,\overrightarrow t \) vuông góc với nhau. Do đó D đúng.
Câu 2:
Góc giữa vectơ \(\overrightarrow a \left( { - 1; - 1} \right)\) và vecto \(\overrightarrow b \left( { - 1;0} \right)\) có số đo bằng:
Đáp án đúng là D
Ta có: \(\overrightarrow a .\overrightarrow b = \left( { - 1} \right).\left( { - 1} \right) + \left( { - 1} \right).0 = 1,\left| {\overrightarrow a } \right| = \sqrt {{{\left( { - 1} \right)}^2} + {{\left( { - 1} \right)}^2}} = \sqrt 2 ,\left| {\overrightarrow b } \right| = \sqrt {{{\left( { - 1} \right)}^2} + {0^2}} = 1.\)
\( \Rightarrow cos\left( {\overrightarrow a .\overrightarrow b } \right) = \frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}} = \frac{1}{{\sqrt 2 }} \Rightarrow \left( {\overrightarrow a .\overrightarrow b } \right) = 45^\circ .\)
Vậy góc giữa hai vec tơ \(\overrightarrow a \) và \(\overrightarrow b \)là 45°.
Câu 3:
Cho hình vuông ABCD có độ dài cạnh là a và A(0; 0), B(a; 0), C(a; a), D(0; a). Khẳng định nào sau đây là đúng?
Đáp án đúng là B
Vì ABCD là hình vuông cạnh a nên AB = BC = a, BD = AC = a\(\sqrt 2 \).
Ta có \(\overrightarrow {AB} \left( {a;\,\,0} \right)\), \(\overrightarrow {BD} \left( { - a;\,\,a} \right)\), \(\overrightarrow {AC} \left( {a;\,\,a} \right)\), \(\overrightarrow {BC} \left( {0;\,\,a} \right)\), \(\overrightarrow {BA} \left( { - a;\,\,0} \right)\).
Khi đó:
+) \(\overrightarrow {AB} .\overrightarrow {BD} = a.\left( { - a} \right) + 0.a = - {a^2}\)
\( \Rightarrow \cos \left( {\overrightarrow {AB} ,\overrightarrow {BD} } \right) = \frac{{\overrightarrow {AB} .\overrightarrow {BD} }}{{\left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {BD} } \right|}} = \frac{{ - {a^2}}}{{a.a\sqrt 2 }} = \frac{{ - 1}}{{\sqrt 2 }} \Rightarrow \left( {\overrightarrow {AB} ,\overrightarrow {BD} } \right) = {135^0}.\) Do đó A sai.
+) \(\overrightarrow {AC} .\overrightarrow {BC} \) = a.0 + a.a = a2
\( \Rightarrow \cos \left( {\overrightarrow {AC} ,\overrightarrow {BC} } \right) = \frac{{\overrightarrow {AC} .\overrightarrow {BC} }}{{\left| {\overrightarrow {AC} } \right|.\left| {\overrightarrow {BC} } \right|}} = \frac{{{a^2}}}{{a.a\sqrt 2 }} = \frac{1}{{\sqrt 2 }} \Rightarrow \left( {\overrightarrow {AC} ,\overrightarrow {BC} } \right) = {45^0}.\) Do đó B đúng
+) \(\overrightarrow {AC} .\overrightarrow {BD} = a.\left( { - a} \right) + a.a = 0\). Do đó C sai.
+) \(\overrightarrow {BA} .\overrightarrow {BD} \) = -a.(-a) + 0.a = a2. Do đó D sai.
Câu 4:
Khi nào thì hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) vuông góc?
Đáp án đúng là C
Hai vec tơ \(\overrightarrow a \) và \(\overrightarrow b \) vuông góc khi \(\overrightarrow a \).\(\overrightarrow b \)= 0.
Câu 5:
Trong mặt phẳng tọa độ Oxy, cho điểm A(-1; 3), B(0; 4) và C(2x – 1; 3x2). Tổng các giá trị của x thỏa mãn \(\overrightarrow {AB} .\overrightarrow {AC} = 2\)
Đáp án đúng là A
Ta có: \(\overrightarrow {AB} \left( {1;1} \right),\overrightarrow {AC} \left( {2x;3{x^2} - 3} \right)\).
Khi đó: \(\overrightarrow {AB} .\overrightarrow {AC} \) = 1.2x + 1.(3x2 – 3) = 3x2 + 2x – 3
Mà \(\overrightarrow {AB} .\overrightarrow {AC} \) = 2 nên 3x2 + 2x – 3 = 2
⇔ 3x2 + 2x – 5 = 0
\( \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - \frac{5}{3}\end{array} \right.\)
Tổng hai nghiệm là 1 + \(\left( { - \frac{5}{3}} \right)\) = \(\frac{3}{3} + \left( { - \frac{5}{3}} \right) = - \frac{2}{3}.\)
Vậy tổng hai nghiệm là \( - \frac{2}{3}.\)
Câu 6:
Khi nào tích vô hướng của hai vecto \(\overrightarrow u ,\overrightarrow v \) là một số dương.
Đáp án đúng là D
Tích vô hướng của hai vecto \(\overrightarrow u ,\overrightarrow v \ne \overrightarrow 0 \) được tính bởi công thức sau:
\(\overrightarrow u .\overrightarrow v = \left| {\overrightarrow u } \right|.\left| {\overrightarrow v } \right|.c{\rm{os}}\left( {\overrightarrow u ,\overrightarrow v } \right).\)
Vì \(\left| {\overrightarrow u } \right| > 0,\left| {\overrightarrow v } \right| > 0\) nên dấu của \(\overrightarrow u .\overrightarrow v \) phụ thuộc vào dấu của \(c{\rm{os}}\left( {\overrightarrow u ,\overrightarrow v } \right)\).
Nếu tích vô hướng của hai vecto \(\overrightarrow u ,\overrightarrow v \) là một số dương thì \(c{\rm{os}}\left( {\overrightarrow u ,\overrightarrow v } \right) > 0.\) Do đó góc giữa hai vecto \(\overrightarrow u ,\overrightarrow v \) là góc nhọn hoặc bằng 00.
Câu 7:
Khi nào thì \({\left( {\overrightarrow u .\overrightarrow v } \right)^2} = {\overrightarrow u ^2}.{\overrightarrow v ^2}?\)
Đáp án đúng là B
Ta có: \(\overrightarrow u .\overrightarrow v = \left| {\overrightarrow u } \right|.\left| {\overrightarrow v } \right|.c{\rm{os}}\left( {\overrightarrow u ,\overrightarrow v } \right)\)
\( \Leftrightarrow {\left( {\overrightarrow u .\overrightarrow v } \right)^2} = {\left[ {\left| {\overrightarrow u } \right|.\left| {\overrightarrow v } \right|.c{\rm{os}}\left( {\overrightarrow u ,\overrightarrow v } \right)} \right]^2} = {\overrightarrow u ^2}.{\overrightarrow v ^2}.c{\rm{o}}{{\rm{s}}^2}\left( {\overrightarrow u ,\overrightarrow v } \right)\)
Để \({\left( {\overrightarrow u .\overrightarrow v } \right)^2} = {\overrightarrow u ^2}.{\overrightarrow v ^2}\) thì \(c{\rm{o}}{{\rm{s}}^2}\left( {\overrightarrow u ,\overrightarrow v } \right) = 1 \Leftrightarrow \left[ \begin{array}{l}c{\rm{os}}\left( {\overrightarrow u ,\overrightarrow v } \right) = 1\\c{\rm{os}}\left( {\overrightarrow u ,\overrightarrow v } \right) = - 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left( {\overrightarrow u ,\overrightarrow v } \right) = {0^0}\\\left( {\overrightarrow u ,\overrightarrow v } \right) = {180^0}\end{array} \right.\)
Vậy khi góc giữa hai vecto \(\overrightarrow u ,\overrightarrow v \) là 00 hoặc 1800 thì \({\left( {\overrightarrow u .\overrightarrow v } \right)^2} = {\overrightarrow u ^2}.{\overrightarrow v ^2}.\)
Câu 8:
Cho tam giác ABC có BC = a, CA = b, AB = c. Hãy tính \(\overrightarrow {AB} .\overrightarrow {AC} \) theo a, b, c.
Đáp án đúng là D
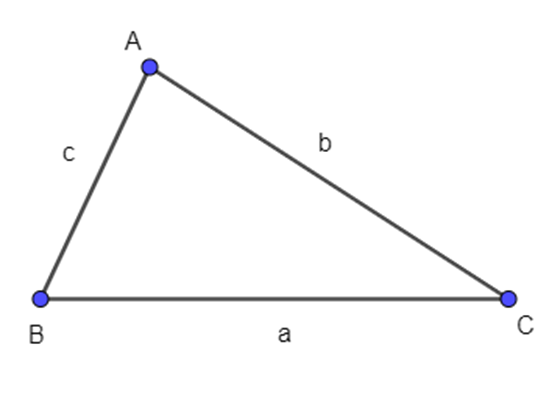
Ta có: \(\overrightarrow {AB} .\overrightarrow {AC} = AB.AC.c{\rm{os}}\left( {\overrightarrow {AB} .\overrightarrow {AC} } \right) = AB.AC.\cos BAC = bc.c{\rm{osBAC}}\)
Theo định lí cos, ta có:
\[{\rm{cosBAC = }}\frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}\]
\(\overrightarrow {AB} .\overrightarrow {AC} = bc.\frac{{{b^2} + {c^2} - {a^2}}}{{2bc}} = \frac{{{b^2} + {c^2} - {a^2}}}{2}\).
Vậy \(\overrightarrow {AB} .\overrightarrow {AC} = \frac{{{b^2} + {c^2} - {a^2}}}{2}.\)
Câu 9:
Tính tích vô hướng của hai vectơ \(\overrightarrow u \left( {1; - 3} \right),\overrightarrow v \left( {\sqrt 7 ;\,\, - 2} \right)\) là k. Nhận xét nào sau đây đúng về giá trị của k.
Đáp án đúng là D
Tích vô hướng của hai vecto \(k = \overrightarrow u .\overrightarrow v = 1.\sqrt 7 + \left( { - 3} \right).\left( { - 2} \right) = \sqrt 7 + 6.\)
Do đó k là số vô tỉ.
Câu 10:
Trong mặt phẳng tọa độ Oxy, hãy tính góc giữa hai vecto \(\overrightarrow a \) và \(\overrightarrow b \) trong trường hợp \(\overrightarrow a \left( {3;1} \right),\overrightarrow b \left( {2;4} \right)\).
Đáp án đúng là B
Ta có: \(\overrightarrow a .\overrightarrow b = 3.2 + 1.4 = 10\)
\(\left| {\overrightarrow a } \right| = \sqrt {{3^2} + {1^2}} = \sqrt {10} ,\left| {\overrightarrow b } \right| = \sqrt {{2^2} + {4^2}} = 2\sqrt 5 \)
\(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.c{\rm{os}}\left( {\overrightarrow a ,\overrightarrow b } \right) \Rightarrow c{\rm{os}}\left( {\overrightarrow a ,\overrightarrow b } \right) = \frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}} = \frac{{10}}{{\sqrt {10} .2\sqrt 5 }} = \frac{1}{{\sqrt 2 }} \Rightarrow \left( {\overrightarrow a ,\overrightarrow b } \right) = {45^0}.\)
Câu 11:
Đáp án đúng là C
Vì I là trung điểm của AB nên ta có: \(\overrightarrow {IA} + \overrightarrow {IB} = \overrightarrow 0 \) hay \(\overrightarrow {IB} = - \overrightarrow {IA} \).
Xét \(\overrightarrow {MA} .\overrightarrow {MB} = \left( {\overrightarrow {MI} + \overrightarrow {IA} } \right).\left( {\overrightarrow {MI} + \overrightarrow {IB} } \right)\)
\( = {\overrightarrow {MI} ^2} + \overrightarrow {MI} .\overrightarrow {IB} + \overrightarrow {MI} .\overrightarrow {IA} + \overrightarrow {IB} .\overrightarrow {IA} \)
\( = {\overrightarrow {MI} ^2} + \overrightarrow {MI} .\left( {\overrightarrow {IB} + \overrightarrow {IA} } \right) + \overrightarrow {IB} .\overrightarrow {IA} \)
\( = {\overrightarrow {MI} ^2} + \left( { - \overrightarrow {IA} } \right).\overrightarrow {IA} \)
\( = {\overrightarrow {MI} ^2} - {\overrightarrow {IA} ^2}\)
\( = M{I^2} - I{A^2}\).
Câu 12:
Cho tam giác ABC với A(-1;2), B(8;-1), C(8;8). Tính bán kính đường tròn ngoại tiếp tam giác ABC.
Đáp án đúng là C
Ta có:
\(\overrightarrow {AB} = \left( {9; - 3} \right) \Rightarrow AB = \sqrt {{9^2} + {{\left( { - 3} \right)}^2}} = 3\sqrt {10} .\)
\(\overrightarrow {AC} \left( {9;6} \right) \Rightarrow AC = \sqrt {{9^2} + {6^2}} = 3\sqrt {13} .\)
\(\overrightarrow {BC} \left( {0;9} \right) \Rightarrow BC = \sqrt {{0^2} + {9^2}} = 9.\)
Ta lại có:
\(\overrightarrow {AB} .\overrightarrow {AC} = AB.AC.cos\widehat {BAC}\)
\( \Leftrightarrow 9.9 + \left( { - 3} \right).6 = 3\sqrt {10} .3\sqrt {13} .cos\widehat {BAC}\)
\( \Leftrightarrow 63 = 9\sqrt {130} .cos\widehat {BAC}\)
\( \Leftrightarrow cos\widehat {BAC} = \frac{7}{{\sqrt {130} }} \Leftrightarrow \widehat {BAC} \approx 52,13^\circ .\)
Áp dụng định lí Sin trong tam giác ta được:
\(\frac{{BC}}{{\sin \widehat {BAC}}} = 2R \Leftrightarrow \frac{9}{{\sin 52,13^\circ }} = 2R \Leftrightarrow R \approx 5,7\).
Câu 13:
Tìm điều kiện của \(\overrightarrow u ,\overrightarrow v \) để \(\overrightarrow u .\overrightarrow v = - \left| {\overrightarrow u } \right|.\left| {\overrightarrow v } \right|.\)
Đáp án đúng là A
Ta có: \(\overrightarrow u .\overrightarrow v = \left| {\overrightarrow u } \right|.\left| {\overrightarrow v } \right|.\cos \left( {\overrightarrow u ,\overrightarrow v } \right)\)
Để \(\overrightarrow u .\overrightarrow v = - \left| {\overrightarrow u } \right|.\left| {\overrightarrow v } \right|\) thì \(\cos \left( {\overrightarrow u ,\overrightarrow v } \right) = - 1 \Leftrightarrow \left( {\overrightarrow u ,\overrightarrow v } \right) = {180^0}\)
Suy ra \(\overrightarrow u ,\overrightarrow v \) là hai vectơ ngược hướng.
Câu 14:
Trong mặt phẳng tọa độ Oxy, cho hai điểm A(1; -3), B(5; 2). Tìm điểm M thuộc tia Oy để góc \(\widehat {AMB} = {90^0}.\)
Đáp án đúng là D
Gọi M có tọa độ M(0; m).
Vì M thuộc tia Oy nên m ≥ 0.
Ta có: \(\overrightarrow {AM} \left( { - 1;m + 3} \right),\overrightarrow {BM} \left( { - 5;m - 2} \right)\).
\( \Rightarrow \overrightarrow {AM} .\overrightarrow {BM} = \left( { - 1} \right).\left( { - 5} \right) + \left( {m + 3} \right).\left( {m - 2} \right) = {m^2} + m - 1.\)
Để \(\widehat {AMB} = {90^0}\) thì \(\overrightarrow {AM} .\overrightarrow {BM} = 0\)
\( \Leftrightarrow {m^2} + m - 1 = 0 \Leftrightarrow \left[ \begin{array}{l}m = \frac{{ - 1 + \sqrt 5 }}{2}\\m = \frac{{ - 1 - \sqrt 5 }}{2}\end{array} \right.\)
Ta thấy \(m = \frac{{ - 1 + \sqrt 5 }}{2}\) (thỏa mãn) và \(m = \frac{{ - 1 - \sqrt 5 }}{2}\) (không thỏa mãn)
Vậy \(M\left( {0;\frac{{ - 1 + \sqrt 5 }}{2}} \right)\).
Câu 15:
Cho tam giác ABC có trọng tâm G. Với điểm M bất kì, đẳng thức nào sau đây đúng?
Đáp án đúng là A
\(M{A^2} + {\rm{ }}M{B^2} + {\rm{ }}M{C^2} = {\overrightarrow {MA} ^2} + {\overrightarrow {MB} ^2} + {\overrightarrow {MC} ^2}\)
\( = {\left( {\overrightarrow {MG} + \overrightarrow {GA} } \right)^2} + {\left( {\overrightarrow {MG} + \overrightarrow {GB} } \right)^2} + {\left( {\overrightarrow {MG} + \overrightarrow {GC} } \right)^2}\)
\( = {\overrightarrow {MG} ^2} + 2\overrightarrow {MG} .\overrightarrow {GA} + {\overrightarrow {GA} ^2} + {\overrightarrow {MG} ^2} + 2\overrightarrow {MG} .\overrightarrow {GB} + {\overrightarrow {GB} ^2} + {\overrightarrow {MG} ^2} + 2\overrightarrow {MG} .\overrightarrow {GC} + {\overrightarrow {GC} ^2}\)
\( = 3{\overrightarrow {MG} ^2} + 2\overrightarrow {MG} .\left( {\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} } \right) + {\overrightarrow {GA} ^2} + {\overrightarrow {GB} ^2} + {\overrightarrow {GC} ^2}\)
Ta có: \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \) (tính chất trọng tâm tam giác)
\( \Rightarrow \overrightarrow {MG} .\left( {\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} } \right) = \overrightarrow {MG} .\overrightarrow 0 = 0\)
\( \Rightarrow M{A^2} + {\rm{ }}M{B^2} + {\rm{ }}M{C^2} = 3{\overrightarrow {MG} ^2} + {\overrightarrow {GA} ^2} + {\overrightarrow {GB} ^2} + {\overrightarrow {GC} ^2}.\)
Câu 16:
Trong mặt phẳng tọa độ Oxy, cho ba điểm không thẳng hàng A(-3;1), B(2;4), C(2;-2). Gọi H(x; y) là trực tâm của tam giác ABC. Tính S = 5x + y.
Đáp án đúng là C
Gọi trực tâm H của tam giác ABC có tọa độ là H(x;y)
Khi đó, ta có: \(\overrightarrow {AH} \left( {x + 3;y - 1} \right);\overrightarrow {BC} \left( {0; - 6} \right);\overrightarrow {BH} \left( {x - 2;y - 4} \right);\overrightarrow {AC} \left( {5; - 3} \right)\)
Vì \(AH \bot BC \Rightarrow \overrightarrow {AH} .\overrightarrow {BC} = 0 \Leftrightarrow \left( {x + 3} \right).0 + \left( {y - 1} \right).\left( { - 6} \right) = 0 \Leftrightarrow y = 1.\)
Vì \(BH \bot AC \Rightarrow \overrightarrow {BH} .\overrightarrow {AC} = 0 \Leftrightarrow \left( {x - 2} \right).5 + \left( {y - 4} \right).\left( { - 3} \right) = 0\)
\( \Leftrightarrow 5x - 10 - 3y + 12 = 0\)
\( \Leftrightarrow 5x - 3y = - 2\)
Mà y = 1 \( \Rightarrow 5x - 3.1 = - 2 \Leftrightarrow x = \frac{1}{5}.\)
Suy ra S = 5.\(\frac{1}{5}\) + 1 = 2.
