50 câu trắc nghiệm Hàm số bậc nhất và bậc hai nâng cao (P2)
-
6166 lượt thi
-
25 câu hỏi
-
25 phút
Danh sách câu hỏi
Câu 1:
Cho hàm số Tập xác định của hàm số là:
+ Với x ≤ 0 thì ta có hàm số luôn xác định.
Do đó tập xác định của hàm số
+Với x> 0 thì ta có hàm số luôn xác định.
Do đó tập xác định của hàm số
Kết hợp cả 2 trường hợp; vậy tập xác định là
Chọn C.
Câu 2:
Đỉnh của parabol y =x2+x+m nằm trên đường thẳng y= 3/4 nếu m bằng:
Ta tìm đỉnh của parabol:
Suy ra m=1.
Chọn D.
Câu 3:
Nếu hàm số y= ax2+ bx+c có đồ thị như sau thì dấu các hệ số của nó là:
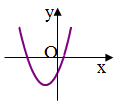
+ Nhận xét đồ thị hướng lên nên a> 0.
+ Giao với Oy tại (0; c) mà điểm đó nằm phía dưới trục hoành nên c<0.
+ Mặt khác; vì a>0 và Đỉnh I nằm bên trái trục hoành nên b>0.
Chọn B.
Câu 4:
Cho đường thẳng d:(9m2-4) x+(n2-9) y=(n-3 )(3m+2). Với giá trị nào của m và n thì phương trình đã cho là đường thẳng song song với trục Ox?
+ Để d song song với Ox thì d phải có dạng by+c=0 với c≠0; b≠0
Chọn C.
Câu 5:
Cho đồ thị: Tìm giá trị lớn nhất và nhỏ nhất của hàm số với -3≤ x≤ 4
Ta có:
+Vẽ đường thẳng y= x với x≥3 đi qua hai điểm O(0; 0) và A(1;1) và lấy phần đường thẳng bên phải của đường thẳng x= 3.
+Vẽ đường thẳng y=5x-12 với 2≤ x≤ 3 đi qua hai điểm B(3;3) và C( 2; -2) và lấy phần đường thẳng nằm giữa của hai đường thẳng x=2; x=3.
+Vẽ đường thẳng y= -x đi qua hai điểm O và D( -1; -1) và lấy phần đường thẳng bên trái của đường thẳng x= 2
+ Dựa vào đồ thị hàm số ta có:
Chọn C.
Câu 6:
Tìm giá trị nhỏ nhất và lớn nhất của các hàm số đó trên [ -2; 2]
Từ đề bài suy ra:
Bảng biến thiên
Ta có y(-2) =5; y(2) =3
Dựa vào bảng biến thiên ta có
Chọn D.
Câu 7:
Tìm tích của giá trị nhỏ nhất và lớn nhất của các hàm số đó trên [ -2;2]
Ta có:
Bảng biến thiên
Ta có y(-2) = -1; y(2) =1
Dựa vào bảng biến thiên ta có
Tích giá trị lớn nhất và giá trị nhỏ nhất là: 1.(-1) = - 1.
Chọn B.
Câu 8:
Cho parabol (P) ; y= ax2+bx+ c biết: (P) đi qua A(2;3) có đỉnh I( 1;2) . Hỏi a+ b+c bằng bao nhiêu.
Vậy (P) cần tìm là y= x2-2x+3.
Chọn D.
Câu 9:
Xác định parabol (P) ; y= ax2+bx+ c biết: c là số nguyên tố chẵn và (P) đi qua B( 3; -4) và có trục đối xứng là
Ta có c là số nguyên tố chẵn nên c= 2
Do (P) đi qua B(3; -4) nên -4=9a+3b+2 (1)
Chọn A.
Câu 10:
Xác định parabol (P) ; y= ax2+bx+ c biết: Hàm số y= ax2+bx+ c có giá trị nhỏ nhất bằng 3/4 khi x=1/2 và nhận giá trị bằng khi x=1.
Chọn D.
Câu 11:
Xác định parabol (P) ; y= ax2+bx+ c biết (P) đi qua M(4;3) cắt Ox tại N(3;0) và P sao cho ∆ INP có diện tích bằng 1 biết hoành độ điểm P nhỏ hơn 3.
Vì (P) đi qua M(4;3) nên 3= 16a+ 4b+c (1)
Mặt khác (P) cắt Ox tại N(3;0) suy ra 0=9a+3b+c (2) , (P) cắt Ox tại P nên P(t; 0) với 0= at2+ bt+c (*) ; (P) cắt Ox tại N và P nên phương trình (*) có 1 nghiệm là t=3 ( hoành độ điểm N)
Từ (1) và (2); vế trừ vế ta có 7a+ b=3 hay b= 3-7a
suy ra:
Thay vào (3) ta có:
Suy ra a= 1; b= -4; c=3.
Vậy (P) cần tìm là y= x2-4x+3.
Chọn B.
Câu 12:
Cho hàm số y=f(x) = ax2+ bx+c. Biểu thức f(x+ 3) -3f( x+ 2) +3f( x+ 1) có giá trị bằng.
Ta có:
f(x+3) = a(x+3)2+ b(x+3) +c=ax2+ (6a+b) x+ 9a+ 3b+c
f(x+2) = a(x+2)2+ b(x+2) +c=ax2+ (4a+b) x+ 4a+ 2b+c
f (x+1) = a(x+1)2+ b(x+1) +c=ax2+ (2a+b) x+ 2a+ 2b+c
Suy ra: (x+ 3) -3f( x+ 2) +3f( x+ 1)= ax2+ bx+ c
Chọn D.
Câu 13:
Cho hàm số y= x2- 6x+8 và đường thẳng y= m. Khẳng định nào đúng.
+Ta có:
Suy ra đồ thị hàm số có đỉnh là I( 3; -1), đi qua các điểm A( 2;0) và B( 4; 0).
Nhận đường thẳng x= 3 làm trục đối xứng và hướng bề lõm lên trên
+Đường thẳng y=m song song hoặc trùng với trục hoành do đó dựa vào đồ thị ta có
-Với m< -1 đường thẳng y= m và parabol không cắt nhau
-Với m= -1 đường thẳng y= m và parabol cắt nhau tại một điểm(tiếp xúc)
Với m> -1 đường thẳng y= m và parabol cắt nhau tại hai điểm phân biệt
Chọn B.
Câu 14:
Parabol (P) có phương trình y= -x2 đi qua A và B có hoành độ lần lượt là và .Cho O là gốc tọa độ. Khi đó:
+ Parabol (P) đi qua A, B có hoành độ
là hai điểm đối xứng nhau qua Oy.
Vậy tam giác AOB cân tại O.
+ Gọi I là giao điểm của AB và Oy suy ra ∆ IOA vuông tại I nên:
Vậy ∆AOB là tam giác đều.
Chọn B.
Câu 15:
Cho phương trình x2+ 2( m+ 3) x+ m2-3=0, m là tham số.
Tìm m để phương trình có hai nghiệm x1; x2 và P = 5( x1+ x2) – 2x1.x2 giá trị lớn nhất.
Bảng biến thiên
Vậy m= -2 là giá trị cần tìm
Chọn B.
Câu 16:
Parabol (P) y= m2x2 và đường thẳng (d) y= -4x-1 cắt nhau tại hai điểm phân biệt ứng với:
+ Phương trình hoành độ giao điểm của parabol (P) và đường thẳng d :
m2x2= -4x -1 hay m2x2+ 4x+1=0 (1)
+ Parabol cắt đường thẳng tại hai điểm phân biệt khi và chỉ khi (1) có hai nghiệm phân biệt:
Chọn C.
Câu 17:
Tìm giá trị nhỏ nhất của hàm số:
Đặt
Khi đó hàm số trở thành y= t2- 3t+1 với t≥ 1.
Bảng biến thiên
Suy ra giá trị nhỏ nhất của hàm số:
khi và chỉ khi t= 3/2 hay
Chọn C.
Câu 18:
Tìm tích của giá trị lớn nhất và nhỏ nhất của hàm số y= x4-4x2-1 trên [ -1; 2].
Bảng biến thiên
Chọn C.
Câu 19:
Tìm tích của giá trị lớn nhất và nhỏ nhất của hàm số y= x4+2x3-x trên [-1;1]
Bảng biến thiên
Từ bảng biến thiên ta có
Chọn B.
Câu 23:
Tìm m để đường thẳng y= m cắt đồ thị hàm số tại điểm một điểm duy nhất.
Lập bảng biến thiên(hoặc vẽ đồ thị) từ đó ta suy đường thẳng y= m cắt đồ thị hàm số
tại một điểm duy nhất khi và chỉ khi m< 0 hoặc m> 1.
Chọn D.
Câu 24:
Giá trị nào của m thì đồ thị hàm số y= x2+ 3x+m cắt trục hoành tại hai điểm phân biệt?
Phương trình hoành độ giao điểm của (P ) và trục hoành:
x2+ 3x+m=0 (1)
+ Để đồ thị cắt trục hoành tại hai điểm phân biệt khi phương trình (1) có hai nghiệm phân biệt
Chọn D.
