Đề thi Giữa kì 1 Toán 10 có đáp án - Đề 2
-
534 lượt thi
-
24 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Trong các bất phương trình dưới đây, bất phương trình nào là bất phương trình bậc nhất hai ẩn?
Đáp án đúng là D
Câu 2:
Cho A = ( - ; B= ( 0; Tập hợp A ∩ B là:
Đáp án đúng là: D
Ta biểu diễn các tập hợp trên trục số như sau:
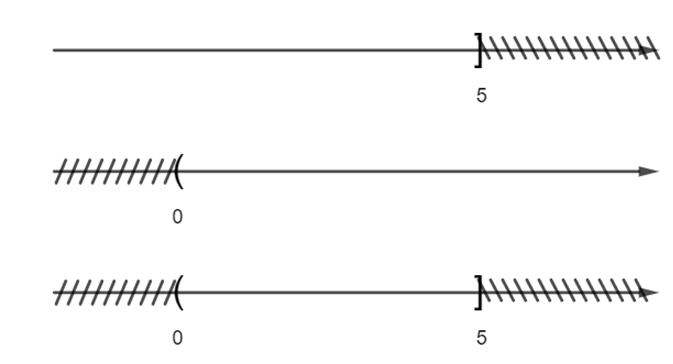
Vậy A ∩ B = (0; 5].
Câu 4:
Tính giá trị biểu thức sau: M = sin75° + tan45° + cos165°.
Đáp án đúng là: A
M = sin75° + tan45° + cos165°
= sin75° + 1 + cos(180° – 15°)
= sin75° + 1 – cos15°
= sin75° + 1 – cos(90° – 75°)
= sin75° + 1 – sin75°
= 1.
Câu 5:
Cho hình thoi ABCD có góc DAB = 60 cạnh 2a. Gọi O là giao điểm của hai đường chéo. Mệnh đề nào sau đây sai?
Đáp án đúng là: B
Câu 6:
Cho tam giác ABC với M là trung điểm của BC. Mệnh đề nào sau đây là đúng?
Đáp án đúng là: C
Câu 7:
Cho hình bình hành ABCD, có AB = 4, BC = 5, BD = 7. Độ dài của AC gần nhất với giá trị nào sau đây:
Đáp án đúng là: C
Câu 9:
Cho tập M = {1; 2; 3; 4; 5} và tập N = {3; 4; 5}. Số các tập X có 4 phần tử thỏa mãn N ⊂ X ⊂ M là :
Đáp án đúng là: B
Vì N ⊂ X nên X phải chứa phần tử của tập hợp N nên X có ít nhất ba phần tử là 3 ; 4 ; 5.
Mặt khác X ⊂ M và X có bốn phần tử nên ta có :
X = {1; 3; 4; 5} hoặc X = {2; 3; 4; 5}.
Vậy có hai tập hợp X thỏa mãn.
Câu 12:
Trong các câu sau, câu nào không phải là mệnh đề ?
Đáp án đúng là: A
Câu A là câu cảm thán không xác định được tính đúng sai nên không phải mệnh đề.
Câu 13:
Cặp số nào sau đây không là nghiệm của hệ bất phương trình
Đáp án đúng là: C
+) Cặp số (0; 0):
Thay x = 0 và y = 0 vào từng bất phương trình trong hệ ta thấy đều thỏa mãn.
Do đó (0; 0) là nghiệm của hệ bất phương trình.
+) Cặp số (1; 1):
Thay x = 1 và y = 1 vào từng bất phương trình trong hệ ta thấy đều thỏa mãn.
Do đó (1; 1) là nghiệm của hệ bất phương trình.
+) Cặp số (– 1; 1):
Thay x = – 1 và y = 1 vào từng bất phương trình trong hệ ta thấy cặp số không thỏa mãn bất phương trình 2x – 3y > – 2.
Do đó (– 1; 1) là nghiệm của hệ bất phương trình.
+) Cặp số (– 1; – 1):
Thay x = – 1 và y = – 1 vào từng bất phương trình trong hệ ta thấy đều thỏa mãn.
Do đó (– 1; – 1) là nghiệm của hệ bất phương trình.
Câu 15:
Cho A = {x ∈ ℕ| x chia hết cho 3 và x chia hết cho 2}, B = {x ∈ ℕ| x chia hết cho 12}. Nhận xét nào dưới đây là đúng?
Đáp án đúng là: B
Tập hợp A gồm các số tự nhiên chia hết cho 2 và chia hết cho 3 nên A là tập các số chia hết cho 6.
Tập hợp B là tập gồm các số tự nhiên chia hết cho 12.
Mà các số chia hết cho 12 thì cũng chia hết cho 6, nhưng chia hết cho 6 chưa chắc chia hết cho 12. Do đó B ⊂ A.
Câu 16:
Miền nghiệm của hệ bất phương trình là:
Đáp án đúng là: A
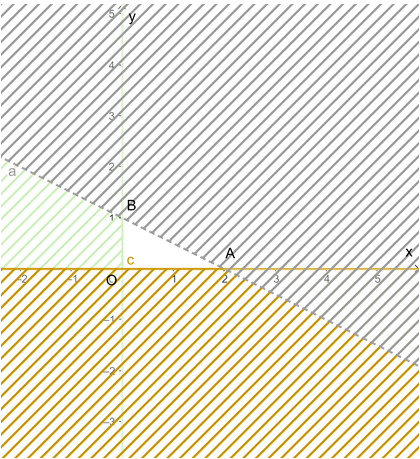
Miền nghiệm của hệ bất phương trình là miền trong tam giác OAB với A(2; 0), B(0; 1) và O (0; 0).
Câu 17:
Với tam giác ABC có bao nhiêu vectơ khác vectơ - không có điểm đầu và điểm cuối là ba đỉnh của tam giác?
Đáp án đúng là: A
Câu 19:
Cho các điểm phân biệt A, B, C, D. Đẳng thức nào sau đây đúng ?
Đáp án đúng là: C
Câu 20:
Cho tam giác ABC có BC = 24, AC = 13, AB = 15. Nhận xét nào sau đây đúng về tam giác ABC.
Đáp án đúng là: D
Câu 21:
Xét mệnh đề P: “∃ x ∈ ℝ: 2x – 3 ≥ 0”. Mệnh đề phủ định của mệnh đề P là
Đáp án đúng là: B
Câu 22:
Ta có: A ∪ B = {0; 1; 2; 3; 4; 5; 6}.
A ∩ B = {2; 3; 4; 5}.
Câu 23:
Tìm m để A = (m – 1; 2] là tập con của tập B = (0; m + 9).
Để A là tập con của tập B thì .
Vậy với m > 1 thì tập A là tập con của tập B.
Câu 24:
+) Biểu diễn miền nghiệm
Vẽ bốn đường thẳng:
d1: x = 1, d2: x = 4, d3: x + y = 5, d4: y = 0.
Biểu diễn từng miền nghiệm của mỗi bất phương trình trên mặt phẳng Oxy.
Miền không gạch chéo (hay chính là miền trong của tứ giác OABC với O(0; 0), A(5; 0), B(4; 1), C(5; 0) và bao gồm cả các cạnh trong hình vẽ là phần giao của các miền nghiệm và cũng là phần biểu diễn miền nghiệm của hệ bất phương trình đã cho.
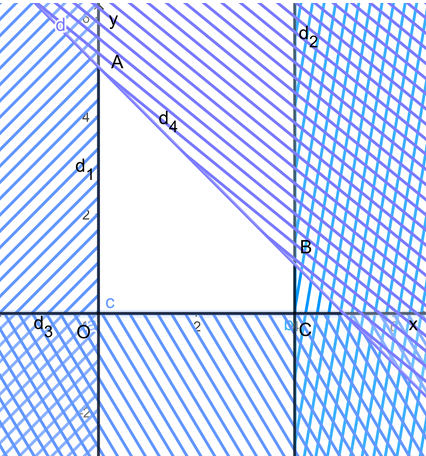
Ta chứng minh được giá trị lớn nhất và giá trị nhỏ nhất của biểu thức F đạt được trên các đỉnh của tứ giác OABC. Khi đó ta có:
Tại O(0; 0): F(0; 0) = 5.0 – 10.0 = 0;
Tại A(0; 5): F(0; 5) = 5.0 – 10.5 = – 50;
Tại B(4; 1): F(4; 1) = 5.4 – 10.1 = 10;
Tại C(5; 0): F(5; 0) = 5.5 – 10.0 = 25.
Vậy giá trị lớn nhất của F là 25 khi x = 5 và y = 0, giá trị nhỏ nhất của F là – 50 khi x = 0, y = 5.
