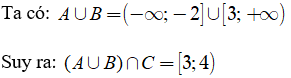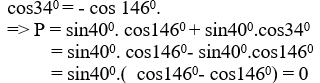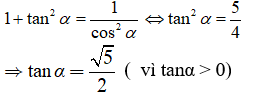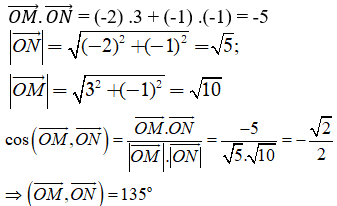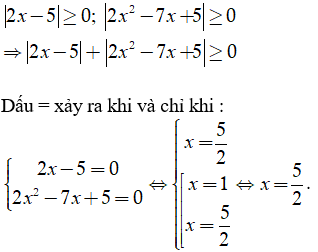Đề thi Toán lớp 10 Học kì 1 năm 2020 - 2021 có đáp án (Đề 4)
-
2059 lượt thi
-
41 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 2:
Cho 2 vectơ đơn vị thỏa mãn . Hãy xác định
Đáp án D
Do 2 vecto là 2 vecto đơn vị nên độ dài mỗi vecto là 1.
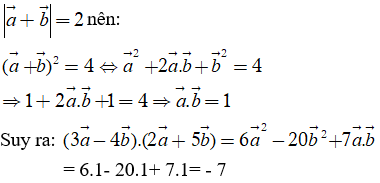
Câu 3:
Mệnh đề nào sau đây là phủ định của mệnh đề: “Mọi động vật đều di chuyển”
Đáp án C
Câu 4:
Điểm nào sau đây thuộc đồ thị hàm số y =
Đáp án A
Xét đáp án A, thay x = 2 và y = 1 vào hàm số ta được: thỏa mãn
Câu 5:
Cho hai vectơ thỏa mãn , và hai vectơ , vuông góc với nhau. Xác định góc α giữa hai vectơ
Đáp án B

Câu 6:
Tìm m để hàm số y = (2m + 1)x + m - 3 đồng biến trên R
Đáp án D
Hàm số bậc nhất y =ax + b đồng biến khi a > 0
Suy ra: 2m + 1 > 0 nên
Câu 8:
Cho hình bình hành ABCD, điểm M thỏa mãn . Khi đó điểm M là
Đáp án A
Do ABCD là hình bình hành nên:
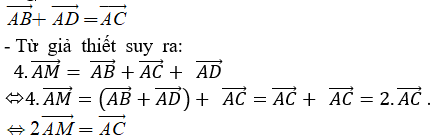
Suy ra: M nằm giữa A và C; AC = 2AM
Do đó: M là trung điểm của AC.
Câu 9:
Tìm tất cả các giá trị thực của tham số m để đường thẳng y = (-3)x + 2m - 3 song song với đường thẳng y = x + 1.
Đáp án C
Để đường thẳng y = (-3)x + 2m - 3 song song với đường thẳng y = x + 1 khi và chỉ khi:
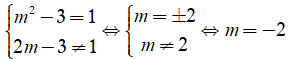
Câu 12:
Cho hai hàm số f(x) = và g(x) = . Mệnh đề nào sau đây đúng?
Suy ra, g(x) không chẵn, không lẻ.
Vậy f(x) là hàm số lẻ; g(x)là hàm số không chẵn, không lẻ.
Câu 14:
Cho tam giác ABC có đường cao BH (H ở trên cạnh AC). Câu nào sau đây đúng
Đáp án C
Ta có BH và CA vuông góc với nhau nên

Câu 15:
Biết rằng đồ thị hàm số y = ax + b đi qua điểm M(1;4) và song song với đường thẳng y = 2x + 1.
Tính tổng S = a + b
Đáp án A
Đồ thị hàm số đi qua điểm M (1;4) nên 4 = a.1 + b (1)
Mặt khác, đồ thị hàm số song song với đường thẳng y = 2x + 1 nên a = 2 (2)
Từ (1) và (2), ta có hệ:
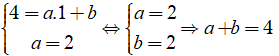
Câu 16:
Trong mặt phẳng Oxy cho A(-1;1); B(1;3) và C(1; -1). Khẳng định nào sau đây đúng.
Đáp án C

Nên tam giác ABC vuông cân tại A.
Câu 17:
Biết rằng đồ thị hàm số y = ax + b đi qua hai điểm M (-1; 3) và N(1; 2). Tính tổng S = a + b.
Đáp án C
Đồ thị hàm số đi qua các điểm M(-1; 3) và N(1; 2) nên:
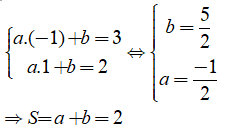
Câu 18:
Tìm tập xác định của hàm số y =
Đáp án B
Hàm số xác định khi:
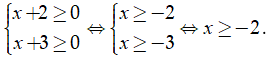
Vậy tập xác định của hàm số là .
Câu 22:
Tìm tất cả các giá trị thực của tham số m để hàm số y = xác định trên khoảng (-1; 3)
Đáp án A
Hàm số xác định khi
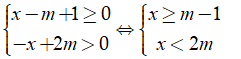
Tập xác định của hàm số là D = [m – 1;2m) với điều kiện m – 1 < 2m hay m > - 1
Hàm số đã cho xác định trên (-1; 3) khi và chỉ khi:
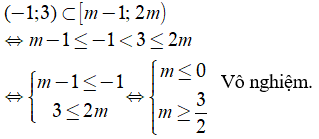
Câu 23:
Trong mặt phẳng tọa độ Oxy, cho 2 điểm A(1; 2) và B(4; 6). Tính khoảng cách giữa hai điểm đó.
Đáp án D
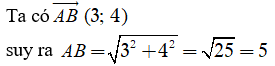
Câu 25:
Tìm tất cả các giá trị thực của m để đường thẳng y = x + 2 cắt đường thẳng y = 4x + 3.
Đáp án B
Để đường thẳng y = x + 2 cắt đường thẳng y = 4x + 3 khi và chỉ khi:
![]()
Câu 26:
Tìm phương trình đường thẳng d: y = ax + b. Biết đường thẳng d đi qua điểm I(2;3) và tạo với hai tia Ox, Oy một tam giác vuông cân.
Đáp án B
Đường thẳng d: y = ax + b đi qua điểm I(2; 3) nên 3 = 2a + b (*)
Ta có:
Câu 28:
Trong mặt phẳng tọa độ Oxy, cho tam giác MNP có M(1;-1), N(5;-3) và P thuộc trục Oy, trọng tâm G của tam giác nằm trên trục Ox.Toạ độ của điểm P là
Đáp án A
Ta có: P thuộc trục Oy => P(0;y), G nằm trên trục Ox => G(x;0)
Vì G là trọng tâm tam giác MNP nên ta có:
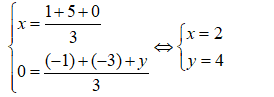
Vậy P(0; 4)
Câu 30:
Cho A (1;2); B (-2;6). Điểm M trên trục Oy sao cho ba điểm A; B; M thẳng hàng thì tọa độ điểm M là:
Đáp án D

Câu 32:
Phương trình - 3|x+1| + 2 = 0 có bao nhiêu nghiệm?
Đáp án D
Vậy phương trình có bốn nghiệm là x = -3; x = 1; x = -2; x = 0
Câu 34:
Phương trình - mx + 1 = 0 có hai nghiệm âm phân biệt khi:
Đáp án A
Phương trình có hai nghiệm âm phân biệt khi:
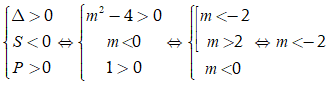
Câu 35:
Tìm tất cả các giá trị thực của tham số m để phương trình 3 - 2(m+1)x + 3m - 5 = 0 có một nghiệm gấp ba nghiệm còn lại.
Đáp án C
Phương trình có hai nghiệm phân biệt:
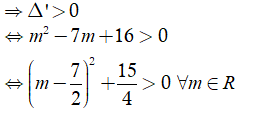
Theo đinh lí Viet, ta có:
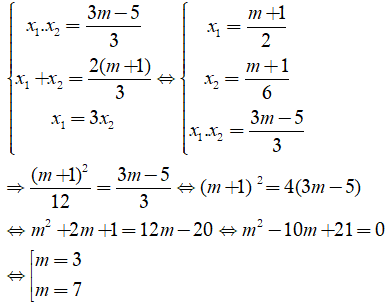
Câu 36:
Cho hàm số f(x) = - 6x + 1. Khi đó:
Đáp án B
Do a = 1 > 0 và –b/2a = 3 nên hàm số giảm trên (-;3) và tăng trên (3;+).
Câu 37:
Tìm tất cả các giá trị thực của tham số m để phương trình (-1)x = m-1 có nghiệm đúng với mọi x thuộc R.
Đáp án A
Phương trình đã cho nghiệm đúng với mọi x hay phương trình có vô số nghiệm khi:
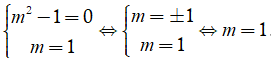
Câu 38:
Cho parabol (P): y = -3 - 6x + 1. Khẳng định đúng nhất trong các khẳng định sau là:
Đáp án D
Ta có = 1 nên (P) có trục đối xứng là x = 1 nên (P) có đỉnh là I(1;2).
Với x = 0 thì y = -1 nên (P) cắt trục tung tại điểm A(0;-1) nên A, B, C đều đúng.
Câu 39:
Cho Parabol (P): y = và đường thẳng y = 2x - 1. Khi đó:
Đáp án A
Phương trình hoành độ giao điểm là:
![]()
Do đó Parabol cắt đường thẳng tại hai điểm phân biệt.
Câu 40:
Tập nghiệm của phương trình là:
Đáp án C
Điều kiện:
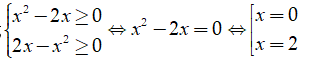
Thử lại ta thấy cả x = 0 và x = 2 đều thỏa mãn phương trình.
Câu 41:
Bảng biến thiên của hàm số y = 3 - 2x + là:
Đáp án A
(Hoặc do a = 3 > 0 nên Parabol có bề lõm lên trên).