8 câu hỏi trắc nghiệm thuộc Trắc nghiệm Toán 10 Bài 2. Hệ bất phương trình bậc nhất hai ẩn (Thông hiểu) có đáp án

Câu 1:

Miền nghiệm của hệ bất phương trình nào sau đây được biểu diễn bởi mặt phẳng không bị gạch trong hình vẽ bên (kể cả đường thẳng d₂ và không kể đường thẳng d₁)?

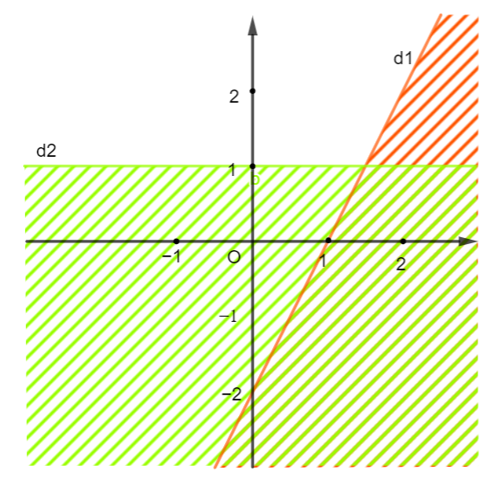
Miền nghiệm của hệ bất phương trình nào sau đây được biểu diễn bởi mặt phẳng không (ảnh 1)

A. $\{\begin{matrix} 2 x + y - 3 < 0 \\ y > 1 \end{matrix}$

B. $\{\begin{matrix} 2 x - y - 2 < 0 \\ y \geq 1 \end{matrix}$

C. $\{\begin{matrix} x - 2 y < 0 \\ y \geq 1 \end{matrix}$

D. $\{\begin{matrix} 2 x - y - 2 < 0 \\ y < 1 \end{matrix}$

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: B

Xét đường thẳng d₁: y = a₁x + b₁ đi qua điểm (1; 0) và (0; −2) nên ta có :

\{\begin{matrix} 0 = 1 a_{1} + b_{1} \\ - 2 = 0 a_{1} + b_{1} \end{matrix} \Leftrightarrow \{\begin{matrix} a_{1} = 2 \\ b_{1} = - 2 \end{matrix}

Vậy (d₁): y = 2x – 2 ⇔ 2x − y − 2 = 0.

Thay điểm (0; 2) thuộc miền nghiệm vào (d₁) ta được:

2 . 0 − 2 − 2 < 0

Do đó ta có bất phương trình 2x − y − 2 < 0 (không kể đường thẳng d₁) (1)

Xét đường thẳng d₂: y = a₂x + b₂ đi qua điểm (1; 1) và (0; 1) nên ta có :

$\{\begin{matrix} 1 = 1 a_{2} + b_{2} \\ 1 = 0 a_{2} + b_{2} \end{matrix} \Leftrightarrow \{\begin{matrix} a_{2} = 0 \\ b_{2} = 1 \end{matrix}$

Vậy (d₂): y = 1.

Thay điểm (0; 2) thuộc miền nghiệm vào (d₂) ta được:

2 > 1

Do đó ta có bất phương trình y ≥ 1 (kể cả đường thẳng d₂) (2)

Từ (1) và (2) ta có hệ bất phương trình cần tìm là: $\{\begin{matrix} 2 x - y - 2 < 0 \\ y \geq 1 \end{matrix}$ .

Câu 2:

Miền nghiệm của bất phương trình nào sau đây được biểu diễn bởi mặt phẳng không bị gạch trong hình vẽ bên (không kể đường thẳng d₁ và d₂)?

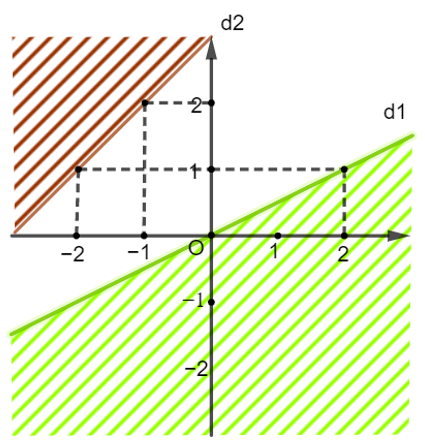
Miền nghiệm của bất phương trình nào sau đây được biểu diễn bởi mặt phẳng không bị (ảnh 1)

A. $\{\begin{matrix} \frac{1}{2} x + y < 0 \\ y < x + 3 \end{matrix}$

B. $\{\begin{matrix} \frac{1}{2} x - y > 0 \\ y < x + 3 \end{matrix}$

C. $\{\begin{matrix} \frac{1}{2} x - y < 0 \\ y < x + 3 \end{matrix}$

D. $\{\begin{matrix} \frac{1}{2} x - y \leq 0 \\ y \leq x + 3 \end{matrix}$

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: C

Xét đường thẳng d₁: y = a₁x + b₁ đi qua điểm (0; 0) và (2; 1) nên ta có :

$\{\begin{matrix} 0 = 0 a_{1} + b_{1} \\ 1 = 2 a_{1} + b_{1} \end{matrix} \Leftrightarrow \{\begin{matrix} a_{1} = \frac{1}{2} \\ b_{1} = 0 \end{matrix}$

Vậy (d₁): y = $\frac{1}{2}$ x ⇔ $\frac{1}{2}$ x − y = 0.

Thay điểm (0; 1) thuộc miền nghiệm vào (d₁) ta được:

$\frac{1}{2}$ . 0 − 1 < 0

Do đó ta có bất phương trình $\frac{1}{2}$ x − y < 0 (không kể đường thẳng d₁) (1)

Xét đường thẳng d₂: y = a₂x + b₂ đi qua điểm (−1; 2) và (−2; 1) nên ta có :

$\{\begin{matrix} 2 = - 1 a_{2} + b_{2} \\ 1 = - 2 a_{2} + b_{2} \end{matrix} \Leftrightarrow \{\begin{matrix} a_{2} = 1 \\ b_{2} = 3 \end{matrix}$

Vậy (d₂): y = x + 3.

Thay điểm (0; 2) thuộc miền nghiệm vào (d₂) ta được:

2 < 0 + 3

Do đó ta có bất phương trình y < x + 3 (không kể đường thẳng d₂) (2)

Từ (1) và (2) ta có hệ bất phương trình $\{\begin{matrix} \frac{1}{2} x - y < 0 \\ y < x + 3 \end{matrix}$ .

Câu 3:

Cho hai bất phương trình x − 5y > 0 (1) và x + y − 1 < 0 (2) và điểm A(3; −1) . Điều nào sau đây là đúng ?

A. Điểm A thuộc miền nghiệm của cả (1) và (2);

B. Điểm A thuộc miền nghiệm của (1) nhưng không thuộc miền nghiệm của (2);

C. Điểm A thuộc miền nghiệm của (2) nhưng không thuộc miền nghiệm của (1);

D. Điểm A không thuộc miền nghiệm của (1) và (2).

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: B

Thay (3; −1) vào bất phương trình (1) ta được:

3 − 5 . (−1) > 0 ⇔ 8 > 0 (luôn đúng)

Thay (3; −1) vào bất phương trình (2) ta được:

3 − 1 − 1 < 0 ⇔ 2 < 0 (vô lí)

Vậy điểm A thuộc miền nghiệm của (1) nhưng không thuộc miền nghiệm của (2).

Câu 4:

Miền nghiệm của hệ bất phương trình nào sau đây được biểu diễn bởi mặt phẳng không bị gạch trong hình vẽ bên (không kể đường thẳng d₁, d₂, d₃)?

A. $\{\begin{matrix} - x + 2 y > 3 \\ x + y - 1 > 0 \\ y > 2 \end{matrix}$

B. $\{\begin{matrix} - x + y > 2 \\ x + y - 1 > 0 \\ y < 2 \end{matrix}$

C. $\{\begin{matrix} x + 2 y > 3 \\ x + y + 3 > 0 \\ y > 2 \end{matrix}$

D. $\{\begin{matrix} - x + 2 y > 2 \\ y - 1 > x \\ y > 2 \end{matrix}$

Xem đáp án

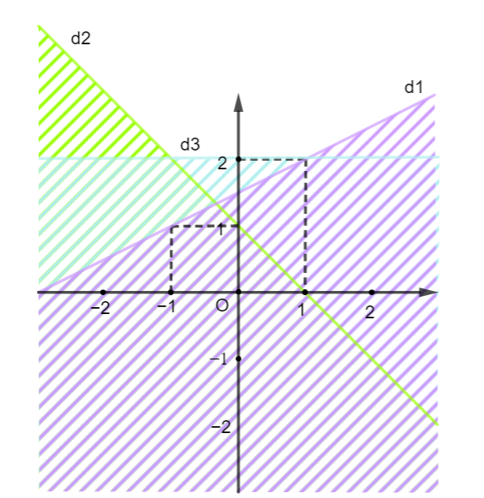
Hướng dẫn giải

Đáp án đúng là: A

Xét đường thẳng d₁: y = a₁x + b₁ đi qua điểm (1; 2) và (−1; 1) nên ta có :

$\{\begin{matrix} 2 = 1 a_{1} + b_{1} \\ 1 = - 1 a_{1} + b_{1} \end{matrix} \Leftrightarrow \{\begin{matrix} a_{1} = \frac{1}{2} \\ b_{1} = \frac{3}{2} \end{matrix}$

Vậy (d₁): y = $\frac{1}{2}$ x + $\frac{3}{2}$ ⇔ −x + 2y = 3.

Thay điểm (0; 3) thuộc miền nghiệm vào (d₁) ta được:

−0 + 2 . 3 > 3

Do đó ta có bất phương trình −x + 2y > 3 (không kể đường thẳng d₁) (1)

Xét đường thẳng d₂: y = a₂x + b₂ đi qua điểm (0; 1) và (1; 0) nên ta có :

$\{\begin{matrix} 1 = 0 a_{2} + b_{2} \\ 0 = 1 a_{2} + b_{2} \end{matrix} \Leftrightarrow \{\begin{matrix} a_{2} = - 1 \\ b_{2} = 1 \end{matrix}$

Vậy (d₂): y = −x + 1 ⇔ x + y − 1 = 0

Thay điểm (0; 3) thuộc miền nghiệm vào (d₂) ta được:

0 + 3 − 1 > 0

Do đó ta có bất phương trình x + y − 1 > 0 (không kể đường thẳng d₂) (2)

Xét đường thẳng d₃: y = a₃x + b₃ đi qua điểm (0; 2) và (1; 2) nên ta có :

$\{\begin{matrix} 2 = 0 a_{1} + b_{1} \\ 2 = 1 a_{1} + b_{1} \end{matrix} \Leftrightarrow \{\begin{matrix} a_{1} = 0 \\ b_{1} = 2 \end{matrix}$

Vậy (d₃): y = 2.

Thay điểm (0; 3) thuộc miền nghiệm vào (d₃) ta được:

3 > 2

Do đó ta có bất phương trình y > 2 (không kể đường thẳng d₃) (3)

Từ (1), (2), (3) ta có hệ bất phương trình $\{\begin{matrix} - x + 2 y > 3 \\ x + y - 1 > 0 \\ y > 2 \end{matrix}$ .

Câu 5:

Phần không bị gạch trong hình bên (không kể đường thẳng d₁ và d₂) biểu diễn miền nghiệm của một hệ bất phương trình bậc nhất hai ẩn. Điểm thuộc miền nghiệm của hệ bất phương trình là:

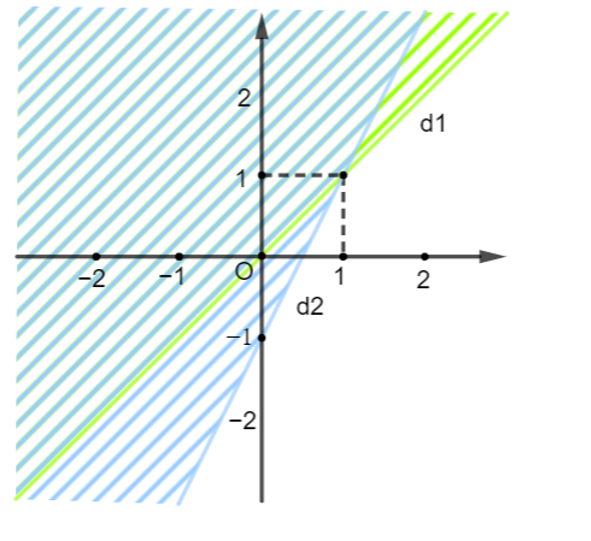
Phần không bị gạch trong hình bên (không kể đường thẳng d1 và d2) biểu diễn miền (ảnh 1)

A. (1; 1);

B. (0; 2);

C. (1; 2);

D. (2; 0).

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: D

Điểm (2; 0) nằm trên mặt phẳng không bị gạch nên (2; 0) thuộc miền nghiệm của hệ bất phương trình trên.

Câu 6:

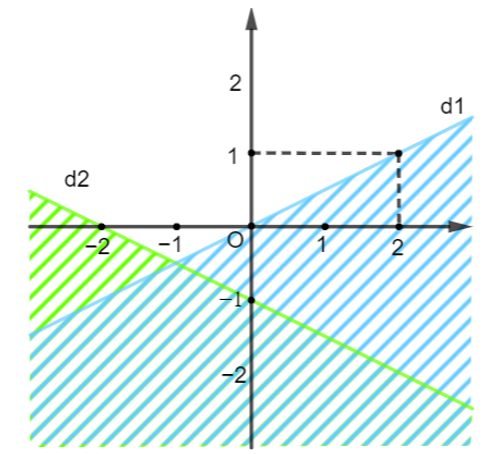
Miền nghiệm của bất phương trình nào sau đây được biểu diễn bởi mặt phẳng không bị gạch trong hình vẽ bên (kể cả đường thẳng d₁ và d₂)?

Miền nghiệm của bất phương trình nào sau đây được biểu diễn bởi mặt phẳng không (ảnh 1)

A. $\{\begin{matrix} x - y \leq 0 \\ x + 2 y \geq 0 \end{matrix}$

B. $\{\begin{matrix} x - 2 y \leq 0 \\ x + 2 y + 2 \geq 0 \end{matrix}$

C. $\{\begin{matrix} x > 0 \\ x + 2 y + 2 \geq 0 \end{matrix}$

D. $\{\begin{matrix} x - 2 y < 0 \\ x + 2 y + 2 > 0 \end{matrix}$

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: B

Xét đường thẳng d₁: y = a₁x + b₁ đi qua điểm (2; 1) và (0; 0) nên ta có :

$\{\begin{matrix} 1 = 2 a_{1} + b_{1} \\ 0 = 0 a_{1} + b_{1} \end{matrix} \Leftrightarrow \{\begin{matrix} a_{1} = \frac{1}{2} \\ b_{1} = 0 \end{matrix}$

Vậy (d₁): y = $\frac{1}{2}$ x ⇔ x − 2y = 0.

Thay điểm (0; 1) thuộc miền nghiệm vào (d₁) ta được:

0 − 2 . 1 < 0

Do đó ta có bất phương trình x − 2y ≤ 0 (kể cả đường thẳng d₁) (1)

Xét đường thẳng d₂: y = a₂x + b₂ đi qua điểm (−2; 0) và (0; −1) nên ta có :

$\{\begin{matrix} 0 = - 2 a_{2} + b_{2} \\ - 1 = 0 a_{2} + b_{2} \end{matrix} \Leftrightarrow \{\begin{matrix} a_{2} = - \frac{1}{2} \\ b_{2} = - 1 \end{matrix}$

Vậy (d₂): y = − $\frac{1}{2}$ x − 1 ⇔ x + 2y + 2 = 0

Thay điểm (−1; 0) thuộc miền nghiệm vào (d₂) ta được:

−1 + 2 . 0 + 2 > 0

Do đó ta có bất phương trình x + 2y + 2 ≥ 0 (kể cả đường thẳng d₂) (2)

Từ (1) và (2) ta có hệ bất phương trình : $\{\begin{matrix} x - 2 y \leq 0 \\ x + 2 y + 2 \geq 0 \end{matrix}$

Câu 7:

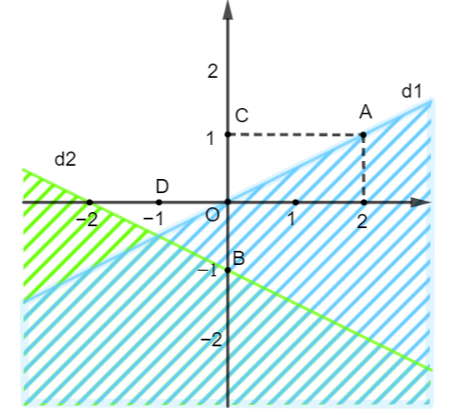
Mặt phẳng không bị gạch trong hình bên (kể cả đường thẳng d₁, không kể đường thẳng d₂) biểu diễn miền nghiệm của một hệ bất phương trình bậc nhất hai ẩn. Điểm không thuộc miền nghiệm của hệ bất phương trình là:

Mặt phẳng không bị gạch trong hình bên (kể cả đường thẳng d1, không kể đường (ảnh 1)

A. A;

B. A và B;

C. C và D;

D. B.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: D

Dễ thấy điểm C và D thuộc phần mặt phẳng không bị gạch nên nó thuộc miền nghiệm của hệ bất phương trình.

Điểm A(2; 1) thuộc đường thẳng d₁ nên nó thuộc miền nghiệm của hệ bất phương trình.

Vì điểm B(0; −1) nằm trên nửa mặt phẳng bị gạch nên B(0; −1) không là nghiệm của hệ bất phương trình trên.

Câu 8:

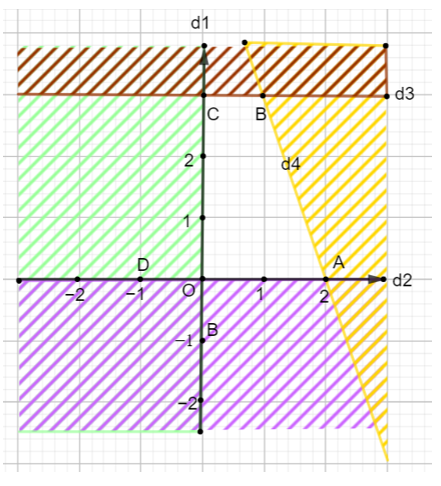
Miền nghiệm của hệ bất phương trình là phần không bị gạch như hình bên. Diện tích đa giác là miền nghiệm của hệ bất phương trình trên đồ thị bằng :

Miền nghiệm của hệ bất phương trình là phần không bị gạch như hình bên. Diện tích (ảnh 1)

A. 5

B. 6

C. $\frac{9}{2}$

D. $\frac{7}{2}$

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: C

Theo hình vẽ, ta thấy miền nghiệm của hệ phương trình là một hình thang vuông.

Ta có :

S_OABC = $\frac{1}{2}$ OC.(OA + BC) = $\frac{1}{2}$ . 3 . (1 + 2) = $\frac{9}{2}$ (đvdt).

CHỌN BỘ SÁCH BẠN MUỐN XEM

Trắc nghiệm Toán 10 Bài 2. Hệ bất phương trình bậc nhất hai ẩn (phần 2) có đáp án

Trắc nghiệm Toán 10 Bài 2. Hệ bất phương trình bậc nhất hai ẩn (Thông hiểu) có đáp án

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương