Trắc nghiệm Toán 10 Bài 2. Tập hợp và các phép toán trên tập hợp (phần 2) có đáp án
Trắc nghiệm Toán 10 Bài 2. Tập hợp và các phép toán trên tập hợp (Thông hiểu) có đáp án
-
823 lượt thi
-
8 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Tập hợp C = {x ∈ ℤ | (x2 – 5x + 4)(x2 x + 3) = 0} có bao nhiêu phần tử?
Hướng dẫn giải
Đáp án đúng là: B
Ta có:
(x2 – 5x + 4)(x2 x + 3) = 0
Vì x ∈ ℤ nên ta loại nghiệm .
⟹ C = {1; 2; 4}.
⟹ n(C) = 3.
Câu 2:
Cho ba tập hợp sau:
A = {m + 1; 2}
B = {1; n – 3}
C = {t; 2}
Hỏi m, n, t nhận giá trị nào sau đây thì A = B = C?
Hướng dẫn giải
Đáp án đúng là: C
Ta thấy tập hợp A có 2 phần tử là m + 1 và 2.
Mà tập hợp B có 2 phần tử là 1 và n – 3.
Do đó để A = B thì .
Ta lại có tập hợp C có 2 phần tử là t và 2.
Do đó để B = C thì t = 1.
Vậy để A = B = C thì m = 0, n = 5, t = 1.
Câu 3:
Cho tập hợp B = {x ∈ ℕ| 3 < 2x – 1 < m}.
Tìm giá trị của m để B là tập hợp rỗng?
Hướng dẫn giải
Đáp án đúng là: B
Xét bất phương trình 3 < 2x – 1 < m (*).
A. Thay m = 7 vào bất phương trình (*) ta có:
3 < 2x – 1 < 7
⟺ 3 + 1 < 2x < 7 + 1
⟺ 4 < 2x < 8
⟺ 2 < x < 4.
Vì x ∈ ℕ nên ta nhận giá trị x = 3.
⟹ m = 7 thì A = {3}.
B. Thay m = 5 vào bất phương trình (*) ta có:
3 < 2x – 1 < 5
⟺ 3 + 1 < 2x < 5 + 1
⟺ 4 < 2x < 6
⟺ 2 < x < 3.
Vì x ∈ ℕ nên không có giá trị của x nào thỏa mãn.
⟹ m = 5 thì B = ∅.
C. Thay m = 9 vào bất phương trình (*) ta có:
3 < 2x – 1 < 9
⟺ 3 + 1 < 2x < 9 + 1
⟺ 4 < 2x < 10
⟺ 2 < x < 5.
Vì x ∈ ℕ nên ta nhận giá trị x = 3 và x = 4.
⟹ m = 7 thì A = {3; 4}.
D. Thay m = 8 vào bất phương trình (*) ta có:
3 < 2x – 1 < 8
⟺ 3 + 1 < 2x < 8 + 1
⟺ 4 < 2x < 9
⟺ 2 < x < .
Vì x ∈ ℕ nên ta nhận giá trị x = 3 và x = 4.
⟹ m = 7 thì A = {3; 4}.
Vậy m = 5 thì B là tập hợp rỗng.
Câu 4:
Trong các tập hợp sau, tập hợp nào không phải là tập hợp rỗng?
Hướng dẫn giải
Đáp án đúng là: D
A. Ta có:
Phương trình x2 + x + 3 = 0 vô nghiệm.
⟹ Tập hợp A không có phần tử nào thỏa mãn.
⟹ C = ∅.
B. Ta có:
x2 + 6x + 5 = 0 ⟺ .
Vì x ∈ ℕ* nên không có phần tử nào thỏa mãn tập hợp trên.
⟹ B = ∅.
C. Ta có:
x(x2 – 5) = 0 ⟺ .
Vì x ∈ ℕ nên không có phần tử nào thỏa mãn tập hợp trên.
⟹ C = ∅.
D. Ta có:
x2 – 9x + 20 = 0 ⟺
Vì x ∈ ℕ* nên hai nghiệm x = 4 và x = 5 đều thỏa mãn.
Do đó tập hợp D có hai phần tử.
⟹ D = {4; 5}.
Vậy chỉ có tập hợp D không phải là tập hợp rỗng.
Câu 5:
Cho các tập hợp:
A = {x ∈ ℤ | -4 ≤ x ≤ 5};
B = {x ∈ ℤ | -2 ≤ x ≤ 6};
C = {x ∈ ℤ | 0 ≤ x ≤ 1}.
Xác định tập hợp X = (A ∩ B)\C. Câu nào sau đây đúng?
Hướng dẫn giải
Đáp án đúng là: C
Ta có:
+ Các phần tử của tập hợp A là -4; -3; -2; -1; 0; 1; 2; 3; 4; 5.
⟹ A = {-4; -3; -2; -1; 0; 1; 2; 3; 4; 5}.
+ Các phần tử của tập hợp B là -2; -1; 0; 1; 2; 3; 4; 5; 6.
⟹ B = {-2; -1; 0; 1; 2; 3; 4; 5; 6}.
+ Các phần tử của tập hợp C là 0; 1.
⟹ C = {0; 1}.
- Giao của hai tập hợp A và B là tập hợp các phần tử thuộc tập hợp A cũng thuộc tập hợp B, do đó các phần tử thuộc tập hợp A ∩ B là -2; -1; 0; 1; 2; 3; 4; 5.
⟹ A ∩ B = {-2; -1; 0; 1; 2; 3; 4; 5}.
- Các phần tử thuộc tập hợp A ∩ B mà không thuộc tập hợp C là -2; -1; 2; 3; 4; 5.
⟹ X = (A ∩ B)\C = {-2; -1; 2; 3; 4; 5}.
Câu 6:
Lớp 10B1 có 7 học sinh giỏi Toán, 5 học sinh giỏi Lý, 6 học sinh giỏi Hóa, 3 học sinh giỏi cả Toán và Lý, 4 học sinh giỏi cả Toán và Hóa, 2 học sinh giỏi cả Lý và Hóa, 1 học sinh giỏi cả 3 môn Toán, Lý, Hóa. Số học sinh giỏi ít nhất một môn (Toán, Lý, Hóa) của lớp 10B1 là:
Hướng dẫn giải
Đáp án đúng là: B
Ta dùng biểu đồ Ven để giải:
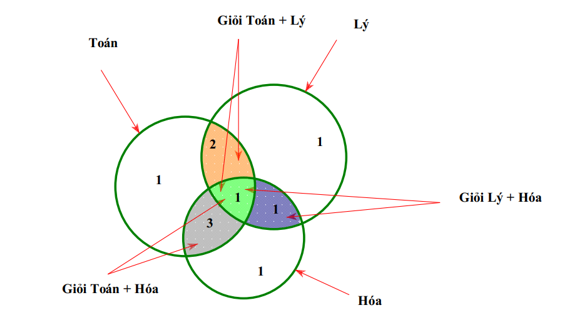
Nhìn vào biểu đồ, số học sinh giỏi ít nhất 1 trong 3 môn là: 1+ 2 + 1 + 3 + 1 + 1 + 1 = 10.
Câu 7:
Trong kì thi học sinh giỏi cấp trường, lớp 11B1 có 15 học sinh giỏi Văn, 22 học sinh giỏi Toán. Tìm số học sinh giỏi cả Văn và Toán biết lớp 11B1 có 40 học sinh, và có 14 học sinh không đạt học sinh giỏi.
Hướng dẫn giải
Đáp án đúng là: C
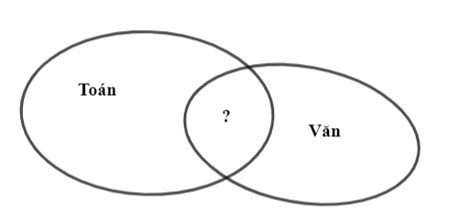
Số học sinh học giỏi ít nhất một trong hai môn Toán và Văn là: 40 - 14 = 26.
Số học sinh chỉ giỏi Toán mà không giỏi Văn (Phần Toán sau khi bỏ đi phần giao)
là: 26 – 15 = 11.
Vậy số học sinh giỏi cả hai môn Toán và Văn (Phần giao nhau) là: 22 – 11 = 11 (học sinh).
Câu 8:
Cho tập hợp A = [4; 7] và B = [2a + 3b – 1; 3a – b + 5] với a, b ∈ ℝ. Khi A = B thì giá trị của biểu thức M = a2 + b2 bằng?
Hướng dẫn giải
Đáp án đúng là: A
Ta có:
A = [4; 7], B = [2a + 3b – 1; 3a – b + 5] với a, b ∈ ℝ.
Khi đó:
A = B ⇔⟹ M = a2 + b2 = 2.
