Trắc nghiệm Toán 10 (có đáp án): Tổng hợp câu hay và khó chương 3 - Phần 2
-
786 lượt thi
-
16 câu hỏi
-
16 phút
Danh sách câu hỏi
Câu 1:
Có tất cả bao nhiêu giá trị nguyên không dương của tham số m để phương trình có nghiệm duy nhất?
Phương trình có nghiệm duy nhất khi hệ có nghiệm duy nhất.
TH1: thì (*) có nghiệm kép (thỏa).
TH2: thì phương trình có nghiệm duy nhất khi (*) có 2 nghiệm thỏa mãn:
Do m không dương nên m ∈ {−1; 0}
Kết hợp với trường hợp m = −3 ở trên ta được 3 giá trị của m thỏa mãn bài toán.
Đáp án cần chọn là: B
Câu 2:
Giả sử phương trình (với m là tham số) có hai nghiệm . Tìm giá trị nhỏ nhất của biểu thức
Phương trình có nên phương trình có hai nghiệm phân biệt với ,
Ta có:
Dấu bằng xảy ra khi m = 0.
Vậy
Đáp án cần chọn là: B
Câu 3:
Gọi S là tập hợp các giá trị của tham số m sao cho parabol (P): cắt Ox tại hai điểm phân biệt A, B thỏa mãn OA = 3OB. Tính tổng T các phần tử của S.
Phương trình hoành độ giao điểm của (P) và Ox:
Để (P) cắt Ox tại hai điểm phân biệt thì (1) có hai nghiệm phân biệt
Giả sử , và
Ta có:
Trường hợp 1: (thỏa mãn)
Trường hợp 2: (thỏa mãn)
Vậy S = −12 + 3 = −9.
Đáp án cần chọn là: D
Câu 4:
Phương trình có bao nhiêu nghiệm?
Thử lại 3 giá trị -5; -6; đều thỏa mãn phương trình
Vậy phương trình đã cho có 3 nghiệm phân biệt
Đáp án cần chọn là: B
Câu 5:
Tập nghiệm của phương trình là:
Đặt
Ta có pt:
So sánh với điều kiện t > 0 ta tìm được
Trường hợp 1:
Trường hợp 2:
Kết hợp hai trường hợp ta được nghiệm x = 1
Đáp án cần chọn là: D
Câu 6:
Tìm m để phương trình có ba nghiệm phân biệt.
+ Khi phương trình cho trở thành:
Do đó: không thỏa mãn đề bài.
+ Khi
Đặt
Phương trình cho trở thành
Phương trình cho có ba nghiệm phân biệt có hai nghiệm thoả
Khi . Do có hai nghiệm phân biệt nên
Với (nhận).
Đáp án cần chọn là: C
Câu 7:
Phương trình có bao nhiêu nghiệm nguyên?
Đặt ta được
Hay phương trình đã cho
Vậy phương trình không có nghiệm nguyên
Đáp án cần chọn là: D
Câu 8:
Cho hàm số có đồ thị (P), và đường thẳng (d) có phương trình . Tìm m để (d) cắt (P) tại hai điểm phân biệt A, B sao cho đạt giá trị nhỏ nhất
Phương trình hoành độ giao điểm:
(d) cắt (P) tại hai điểm phân biệt A, B
Giả sử (*) có hai nghiệm thì
với
Vậy giá trị nhỏ nhất của là khi
Đáp án cần chọn là: A
Câu 9:
Số nghiệm của phương trình là:
Điều kiện:
Đặt
Vậy phương trình đã cho có hai nghiệm
Đáp án cần chọn là: D
Câu 10:
Tập hợp tất cả các giá trị của tham số m để phương trình có nghiệm là:
Điều kiện:
Đặt
Do nên
Trở thành
Để (1) có nghiệm thì (2) có nghiệm
Tức là:
Vậy thì phương trình đã cho có nghiệm
Đáp án cần chọn là: C
Câu 11:
Cho phương trình . Tìm m để phương trình có một nghiệm duy nhất?
Ta có:
Để phương trình (1) có một nghiệm duy nhất thì pt (*) có nghiệm kép
Đáp án cần chọn là: C
Câu 12:
Tổng bình phương các nghiệm của phương trình là:
Điều kiện xác định
Khi đó phương trình
Vậy
Đáp án cần chọn là: B
Câu 13:
Tìm tất cả các giá trị của m để phương trình có nghiệm
Phương trình đã cho tương đương
Đặt
Ta có đồ thị hàm số y = f(x) như sau:
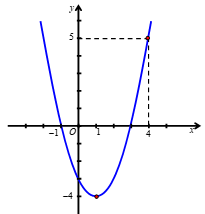
Dựa vào đồ thị, để phương trình có nghiệm x ∈ [0; 4] thì
Đáp án cần chọn là: C
Câu 14:
Cho hàm số f(x) xác định trên R có đồ thị như hình vẽ.
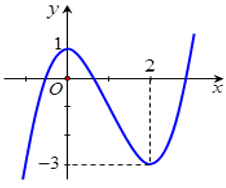
Phương trình có bao nhiêu nghiệm?
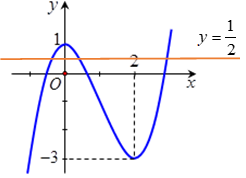
Phương trình đã cho tương đương
Số nghiệm của phương trình là số giao điểm của đồ thị hàm số và đường thẳng
Quan sát đồ thị hàm số ta thấy đường thẳng cắt đồ thị hàm số tại đúng 3 điểm phân biệt.
Vậy phương trình có 3 nghiệm phân biệt.
Đáp án cần chọn là: B
Câu 15:
Tổng các bình phương các nghiệm của phương trình là:
Ta có
Vậy tổng bình phương các nghiệm là
Đáp án cần chọn là: B
Câu 16:
Tìm phương trình đường thẳng . Biết đường thẳng d đi qua điểm I(1; 3) và tạo với hai tia Ox, Oy một tam giác có diện tích bằng 6?
Do đường thẳng d đi qua điểm I (1; 3) nên
Giao điểm của d và các tia Ox, Oy lần lượt là và
(Với b > 0, a < 0 suy ra b > 3)
Do đó: . Mà
Với
Đáp án cần chọn là: A
