Dạng 4: Bài toán có lời văn có đáp án
-
750 lượt thi
-
10 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Bạn Khoa muốn mua một số quần áo mới. Biết những chiếc áo là bằng giá nhau và mỗi chiếc trị giá 100 nghìn đồng, những chiếc quần bằng giá nhau và mỗi chiếc trị giá 150 nghìn đồng. Bạn Khoa chỉ cầm số tiền là 1 triệu đồng. Gọi x là số áo bạn Khoa mua, y là số quần bạn Khoa mua, x, y là số tự nhiên, các bất phương trình mô tả số tiền bạn Khoa mua quần áo là:
Đáp án đúng là: B
Gọi x là số áo bạn Khoa mua, y là số quần bạn Khoa mua nên ta có: x ≥ 0; y ≥ 0.
Để mua x chiếc áo, bạn Khoa phải trả số tiền là: 100 000x (đồng)
Để mua y chiếc quần, bạn Khoa phải trả số tiền là: 150 000y (đồng)
Bạn Khoa chỉ cầm số tiền là 1 triệu đồng nên ta có:
100 000x + 150 000y ≤ 1 000 000
⇔ 10x + 15y ≤ 100
Vậy các bất phương trình mô tả số tiền bạn Khoa mua quần áo là:
10x + 15y ≤ 100; x ≥ 0; y ≥ 0.
Câu 2:
Cô giáo yêu cầu học sinh phải làm ít nhất 15 điểm tích lũy bài tập, phải bao gồm cả bài tập loại dễ và bài tập loại khó. Biết rằng, làm một bài tập loại dễ tích lũy được 2 điểm, làm một bài tập loại khó tích lũy được 5 điểm. Gọi x là số bài tập loại dễ mà học sinh làm, gọi y là số bài tập loại khó mà học sinh làm, x, y là số tự nhiên, các bất phương trình mô tả số điểm tích lũy của học sinh là:
Đáp án đúng là: D.
Gọi x là số bài tập loại dễ mà học sinh làm, gọi y là số bài tập loại khó mà học sinh làm, x, y là số tự nhiên, và số bài tập phải bao gồm cả bài tập loại dễ và bài tập loại khó nên ta có: x > 0; y > 0
Học sinh làm x bài tập loại dễ thì sẽ tích lũy được số điểm là: 2x (điểm)
Học sinh làm y bài tập loại khó thì sẽ tích lũy được số điểm là: 5y (điểm)
Cô giáo yêu cầu học sinh phải làm ít nhất 15 điểm tích lũy bài tập, phải bao gồm cả bài tập loại dễ và bài tập loại khó nên ta có: 2x + 5y ≥ 15
Vậy các bất phương trình mô tả số điểm tích lũy của học sinh là:
2x + 5y ≥ 15; x > 0; y > 0.
Câu 3:
Cô Hằng cần mua phần thưởng tặng các bạn học sinh khá và học sinh giỏi của lớp. Biết số tiền mua phần thưởng không được vượt quá 3 triệu đồng. Biết số học sinh giỏi là 10 em, số học sinh khá là 15 em. Gọi x (đồng) là giá tiền một phần thưởng cho học sinh giỏi, y (đồng) là giá tiền một phần thưởng cho học sinh khá. Các bất phương trình mô tả số tiền mua phần thưởng cho các bạn học sinh khá và giỏi là:
Đáp án đúng là: A.
Gọi x (nghìn) là giá tiền một phần thưởng cho học sinh giỏi, y (nghìn) là giá tiền một phần thưởng cho học sinh khá nên ta có: x > 0; y > 0.
Để mua phần thưởng cho 10 em học sinh giỏi cần chi số tiền là: 10x (nghìn)
Để mua phần thưởng cho 15 em học sinh khá cần chi số tiền là: 15y (nghìn)
Biết số tiền mua phần thưởng không được vượt quá 3 triệu đồng nên ta có:
10x + 15y ≤ 3 000 000
Vậy các bất phương trình mô tả số tiền mua phần thưởng cho các bạn học sinh khá và giỏi là: 10x + 15y ≤ 3 000 000; x > 0; y > 0
Câu 4:
Bạn Vân có tối đa 120 phút để trồng rau trong vườn. Biết có hai loại rau là rau cải và rau muống, rau cải trồng mất 5 phút, rau muống trồng mất 7 phút. Gọi số cây rau cải bạn Vân trồng được là x cây, số cây rau muống bạn Vân trồng được là y cây. Các bất phương trình mô tả thời gian bạn Vân trồng rau là:
Đáp án đúng là: B
Gọi số cây rau cải bạn Vân trồng được là x cây, số cây rau muống bạn Vân trồng được là y cây nên ta có: x ≥ 0; y ≥ 0.
Thời gian Vân trồng x cây rau cải là: 5x (phút)
Thời gian Vân trồng y cây rau muống là: 7y (phút)
Bạn Vân có tối đa 120 phút để trồng rau trong vườn nên ta có: 5x + 7y ≤ 120
Vậy các bất phương trình mô tả thời gian bạn Vân trồng rau là:
5x + 7y ≤ 120; x ≥ 0; y ≥ 0.
Câu 5:
Cửa hàng X bán hai loại nước cam là nước cam loại I và nước cam loại II. Biết để pha chế một cốc nước cam loại I thì cần 3 quả cam, để pha chế một cốc nước cam loại II thì cần 2 quả cam. Cửa hàng chỉ nhập về 50 quả cam. Gọi số cốc nước cam loại I phải pha là x, số cốc nước cam loại II phải là y. Các bất phương trình mô tả số cốc nước cam loại I và loại II cửa hàng pha là:
Gọi số cốc nước cam loại I phải pha là x, só cốc nước cam loại II phải là y nên ta có: x ≥ 0; y ≥ 0
Số cam để pha x cốc nước cam loại I là: 3x
Số cam để pha x cốc nước cam loại II là: 2y
Cửa hàng chỉ nhập về 50 quả cam nên ta có: 3x + 2y ≤ 50
Vậy các bất phương trình mô tả số cốc nước cam loại I và loại II cửa hàng pha là:
3x + 2y ≤ 50; x ≥ 0; y ≥ 0.
Câu 6:
Một khu để xe máy và ô tô có tối đa 50 chỗ đỗ xe. Biết 1 chiếc xe máy ứng với 1 chỗ đỗ, 1 chiếc ô tô ứng với 3 chỗ đỗ. Gọi x là số xe máy vào đỗ, y là số xe ô tô vào đỗ. Các bất phương trình mô tả số chỗ đã được đỗ là:
Đáp án đúng là: A
Gọi x là số xe máy vào đỗ, y là số xe ô tô vào đỗ nên ta có: x ≥ 0; y ≥ 0
Số chỗ đỗ ứng với x chiếc xe máy là: x (chỗ)
Số chỗ đỗ ứng với y chiếc ô tô là: 3y (chỗ)
Khu để xe máy và ô tô có tối đa 50 chỗ đỗ xe nên ta có: x + 3y ≤ 50
Vậy các bất phương trình mô tả số chỗ đã được đỗ là: x + 3y ≤ 50; x ≥ 0; y ≥ 0.
Câu 7:
Một cửa hàng bán đồ chơi gồm hai loại: Đồ chơi loại I và đồ chơi loại II. Biết đồ chơi loại I có giá 100 nghìn đồng, đồ chơi loại II có giá 50 nghìn đồng. Biết cửa hàng phải thu về ít nhất 1 triệu đồng thì mới có lãi. Gọi số đồ chơi loại I bán được là x, số đồ chơi loại II bán được là y. Hỏi trong các giá trị x, y sau đây, giá trị nào tương ứng với cửa hàng có lãi ?
Đáp án đúng là: C
Gọi số đồ chơi loại I bán được là x, số đồ chơi loại II bán được là y nên ta có:
x ≥ 0; y ≥ 0
Số tiền cửa hàng thu về khi bán được x đồ chơi loại I là: 100 000x (đồng)
Số tiền cửa hàng thu về khi bán được x đồ chơi loại II là: 50 000y (đồng)
Biết cửa hàng phải thu về ít nhất 1 triệu đồng thì mới có lãi nên ta có:
100 000x + 50 000y ≤ 1 000 000
⇔ 10x + 5y ≤ 100
Xét cặp số x = 10; y = 0 ta có: 10.10 + 5.0 = 100 ≤ 100
Vậy với x = 10; y = 0 thì cửa hàng có lãi.
Câu 8:
Trong một khu trung tâm thương mại có 30 chỗ bán hàng. Biết 1 cửa hàng đồ chơi chiếm 1 chỗ bán hàng, 1 cửa hàng quần áo chiếm 2 chỗ bán hàng. Với số cửa hàng đồ chơi là 6 thì số cửa hàng quần áo phải là bao nhiêu để phù hợp với khu trung tâm thương mại đó ?
Đáp án đúng là: D
Gọi số cửa hàng quần áo là x (cửa hàng) nên ta có: x ≥ 0
Số chỗ bán hàng ứng với x cửa hàng quần áo là: 2x (chỗ)
Do khu trung tâm thương mại có 30 chỗ bán hàng nên ta có:
6 + 2x ≤ 30
⇔ 2x ≤ 24
⇔ x ≤ 12
Vậy x = 12 phù hợp với yêu cầu đề bài.
Câu 9:
Bạn Lan phải mua một số quyển vở ghi bài, mẹ cho Lan 70 nghìn đồng để mua vở. Biết giá tiền một quyển vở loại đẹp là 7 nghìn đồng, giá tiền một quyển vở loại trung bình là 5 nghìn đồng. Hỏi nếu lan muốn mua 5 quyển vở loại đẹp thì với số tiền còn lại Lan có thể mua tối đa bao nhiêu quyển vở loại trung bình ?
Đáp án đúng là: B
Gọi số quyển vở loại trung bình Lan có thể mua là x (x ≥ 0).
Lan mua 5 quyển vở loại đẹp hết số tiền là: 5 . 7 = 35 (nghìn đồng)
Lan mua x quyển vở loại trung bình hết số tiền là: 5x (nghìn đồng)
Mẹ cho Lan 70 nghìn đồng để mua vở nên ta có:
35 + 5x ≤ 70
⇔ 5x ≤ 35
⇔ x ≤ 7
Vậy với số tiền còn lại Lan có thể mua tối đa 7 quyển vở loại trung bình.
Câu 10:
Một xưởng sản xuất hai loại sản phẩm, mỗi kg sản phẩm loại I cần 2 kg nguyên liệu và 30 giờ, đem lại mức lợi nhuận 40 000 đồng. Mỗi kg sản phẩm loại II cần 4 kg nguyên liệu và 15 giờ, đem lại mức lợi nhuận 30 000 đồng. Xưởng có 200 kg nguyên liệu và 1 200 giờ làm việc. Nên sản xuất mỗi loại sản phẩm bao nhiêu để có mức lợi nhuận cao nhất ?
Đáp án đúng là: A
Gọi x (x ≥ 0 (1)) là số kg loại I cần sản xuất, y (y ≥ 0 (2)) là số kg loại II cần sản xuất.
Số nguyên liệu cần dùng để sản xuất x sản phẩm loại I là: 2x
Số nguyên liệu cần dùng để sản xuất y sản phẩm loại II là: 4y
Xưởng có 200 kg nguyên liệu nên ta có: 2x + 4y ≤ 200 ⇔ x + 2y ≤ 100 ⇔ x + 2y – 100 ≤ 0 (3).
Thời gian để sản xuất x sản phẩm loại I là: 30x
Thời gian để sản xuất y sản phẩm loại II là: 15y
Xưởng có 1 200 giờ làm việc nên ta có: 30x + 15y ≤ 1200 hay 2x + y – 80 ≤ 0 (4)
Xét bất phương trình (1) và điểm A(1; 2) có:
Điểm A không nằm trên đường thẳng x = 0 và 1 ≥ 0, do đó, miền nghiệm của bất phương trình x ≥ 0 là nửa mặt phẳng có kể bờ x = 0 và chứa điểm A(1; 2).
Xét bất phương trình (2) và điểm B(0; 1) có:
Điểm B không nằm trên đường thẳng y = 0 và 1 ≥ 0, do đó, miền nghiệm của bất phương trình y ≥ 0 là nửa mặt phẳng có kể bờ y = 0 và chứa điểm B(0; 1).
Xét bất phương trình (3) và điểm (0; 0) ta có:
Điểm (0; 0) không nằm trên đường thẳng x + 2y – 100 = 0 và 0 + 2.0 – 100 = –100 < 0 nên miền nghiệm của bất phương trình (3) là nửa mặt phẳng có kể bờ x + 2y – 100 = 0 và chứa điểm (0; 0).
Xét bất phương trình (4) và điểm (0; 0) ta có:
Điểm (0; 0) không nằm trên đường thẳng 2x + y – 80 = 0 và 2.0 + 0 – 80 = –80 < 0 nên miền nghiệm của bất phương trình (4) là nửa mặt phẳng có kể bờ 2x + y – 80 = 0 và chứa điểm (0; 0).
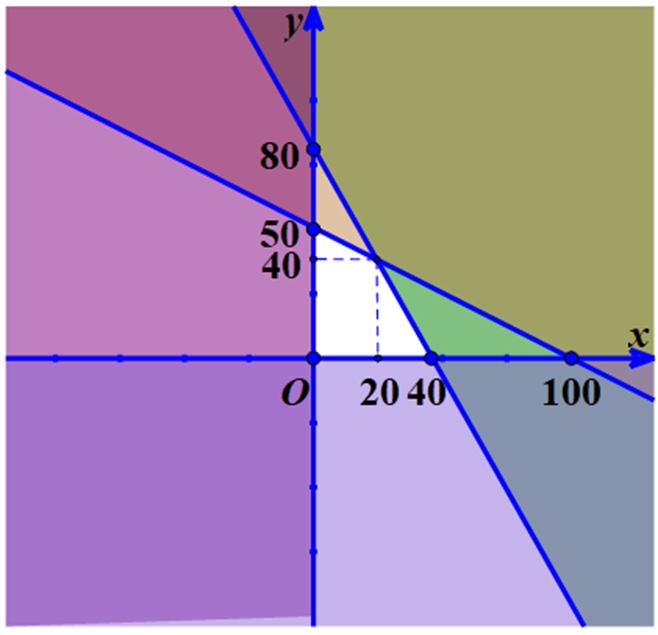
Kết hợp miền nghiệm của các bất phương trình (1), (2), (3) và (4) là miền nghiệm thỏa mãn màu trắng trong hình vẽ:
Lợi nhuận thu lại từ x sản phẩm loại I là: 40 000x
Lợi nhuận thu lại từ y sản phẩm loại II là: 30 000y
Tổng lợi nhuận là: 40 000x + 30 000y
Giá trị lớn nhất của L(x; y) = 40 000x + 30 000y đạt tại một trong các điểm (0; 0), (40; 0), (0; 50), (20; 40).
Ta có:
L(0; 0) = 0
L(40; 0) = 1 600 000
L(0; 50) = 1 500 000
L(20; 40) = 2 000 000
Vậy giá trị lớn nhất của L(x; y) là 2 000 000 khi (x; y) = (20; 40)
Vậy cần sản xuất 20kg sản phẩm loại I và 40kg sản phẩm loại II để có mức lợi nhuận lớn nhất.
