Trắc nghiệm Toán 10 CTST Bài 2. Hàm số bậc hai có đáp án (Thông hiểu)
-
715 lượt thi
-
8 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Hướng dẫn giải
Đáp án đúng là: C
+ Gọi điểm A là giao điểm của parabol (P) và trục hoành.
Suy ra yA = 0.
Vì A ∈ (P) nên \(0 = 2x_A^2 - 4{x_A} + 3\) (vô nghiệm).
Do đó không có điểm A là giao điểm của parabol (P) và trục hoành.
Vì vậy phương án A đúng.
+ Hàm số đã cho có dạng y = ax2 + bx + c, với a = 2, b = –4, c = 3.
Đỉnh S có tọa độ:
⦁ \({x_S} = - \frac{b}{{2a}} = - \frac{{ - 4}}{{2.2}} = 1\);
⦁ yS = 2.12 – 4.1 + 3 = 1.
Suy ra (P) có đỉnh S(1; 1) và có trục đối xứng là x = 1.
Do đó phương án B đúng, C sai.
+ Thay tọa độ điểm M vào hàm số của đồ thị (P) ta được:
9 = 2.(–1)2 – 4.(–1) + 3 (đúng).
Suy ra (P) đi qua điểm M(–1; 9).
Do đó phương án D đúng.
Vậy ta chọn phương án C.
Câu 2:
Cho hàm số y = –x2 – x – 1. Tập giá trị của hàm số đã cho là:
Hướng dẫn giải
Đáp án đúng là: B
Hàm số đã cho có dạng y = ax2 + bx + c, với a = b = c = –1.
Ta có ∆ = b2 – 4ac = (–1)2 – 4.(–1).(–1) = –3.
Suy ra \[\frac{{ - \Delta }}{{4a}} = \frac{{ - \left( { - 3} \right)}}{{4.\left( { - 1} \right)}} = - \frac{3}{4}\].
Vì a = –1 < 0 nên hàm số có giá trị lớn nhất bằng \( - \frac{3}{4}\) và có tập giá trị là \(T = \left( { - \infty ; - \frac{3}{4}} \right]\).
Vậy ta chọn phương án B.
Câu 3:
Hướng dẫn giải
Đáp án đúng là: D
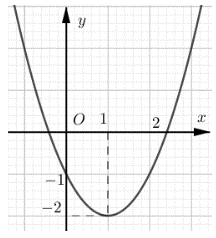
+ Quan sát đồ thị, ta thấy parabol có bề lõm quay lên trên nên a > 0.
Do đó ta loại phương án A vì a = –1 < 0.
+ Quan sát đồ thị, ta thấy parabol có trục đối xứng là đường thẳng x = 1.
⦁ Ở phương án B, đồ thị của hàm số y = x2 + 2x – 2 có trục đối xứng là đường thẳng \(x = - \frac{b}{{2a}} = - \frac{2}{{2.1}} = - 1 \ne 1\).
Do đó ta loại phương án B.
⦁ Ở phương án C, đồ thị của hàm số y = 2x2 – 4x – 2 có trục đối xứng là đường thẳng \(x = - \frac{b}{{2a}} = - \frac{{ - 4}}{{2.2}} = 1\).
• Ở phương án D, đồ thị của hàm số y = x2 – 2x – 1 có trục đối xứng là đường thẳng \(x = - \frac{b}{{2a}} = - \frac{{ - 2}}{{2.1}} = 1\).
+ Quan sát đồ thị, ta thấy parabol đi qua điểm A(0; –1).
• Thay x = 0, y = –1 vào hàm số ở phương án C, ta có: –1 = 2.02 – 4.0 – 2 (vô lí).
Do đó đồ thị của hàm số ở phương án C không đi qua điểm A(0; –1).
Vì vậy ta loại phương án C.
• Thay x = 0, y = –1 vào hàm số ở phương án D, ta có –1 = 02 – 2.0 – 1 (đúng).
Do đó đồ thị của hàm số ở phương án D đi qua điểm A(0; –1).
Vậy ta chọn phương án D.
Câu 4:
Hướng dẫn giải
Đáp án đúng là: C
Hàm số đã cho có dạng y = ax2 + bx + c, với a = m – 1, b = 2m, c = –m2 + 4.
Để hàm số đã cho là hàm số bậc hai thì a ≠ 0.
Nghĩa là, m – 1 ≠ 0.
Suy ra m ≠ 1.
Vậy ta chọn phương án C.
Câu 5:
Parabol (P): y = ax2 + 3x – 2 (a ≠ 0) có trục đối xứng là đường thẳng x = –3 là:
Hướng dẫn giải
Đáp án đúng là: D
Parabol (P): y = ax2 + 3x – 2 (a ≠ 0) có b = 3.
(P) có trục đối xứng là đường thẳng x = –3.
Ta suy ra \( - \frac{b}{{2a}} = 3\).
Tức là, \(\frac{{ - 3}}{{2a}} = - 3\).
Khi đó ta có \(a = \frac{1}{2}\)(thỏa mãn a ≠ 0).
Vậy (P): \(y = \frac{1}{2}{x^2} + 3x - 2\).
Do đó ta chọn phương án D.
Câu 6:
Hướng dẫn giải
Đáp án đúng là: A
Hàm số đã cho có dạng y = ax2 + bx + c, với a = 1, b = –4, c = 5.
Ta có: \( - \frac{b}{{2a}} = - \frac{{ - 4}}{{2.1}} = 2\).
Vì a = 1 > 0 nên ta có hàm số đã cho nghịch biến trên (–∞; 2) và đồng biến trên (2; +∞).
Vậy ta chọn phương án A.
Câu 7:
Bảng biến thiên nào dưới đây là của hàm số y = –x2 + 2x + 1?
Hướng dẫn giải
Đáp án đúng là: C
Hàm số đã cho có dạng y = ax2 + bx + c, với a = –1, b = 2, c = 1.
Đỉnh S có tọa độ:
⦁ \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - 2}}{{2.\left( { - 1} \right)}} = 1\);
⦁ yS = –12 + 2.1 + 1 = 2.
Suy ra S(1; 2).
Vì hàm số bậc hai có a = –1 < 0 nên hàm số đã cho đồng biến trên khoảng (–∞; 1) và nghịch biến trên khoảng (1; +∞).
Ta có bảng biến thiên như sau:
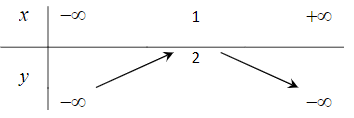
Vậy ta chọn phương án C.
Câu 8:
Hướng dẫn giải
Đáp án đúng là: A
Cách 1:
Hàm số đã cho có dạng y = ax2 + bx + c, với a = –1, b = 2, c = 3.
Ta có ∆ = b2 – 4ac = 4 – 4.(–1).3 = 16.
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai y = f(x) = –x2 + 2x + 3 là một parabol (P):
⦁ Đỉnh S có tọa độ: \({x_S} = - \frac{b}{{2a}} = - \frac{2}{{2.\left( { - 1} \right)}} = 1\) và \({y_S} = - \frac{\Delta }{{4a}} = - \frac{{16}}{{4.\left( { - 1} \right)}} = 4\).
Suy ra tọa độ đỉnh S(1; 4).
⦁ Có trục đối xứng là đường thẳng x = 1 (đường thẳng này đi qua đỉnh S và song song với trục Oy).
⦁ Có bề lõm quay xuống dưới vì a = –1 < 0.
⦁ Cắt trục tung tại điểm có tung độ bằng 3, tức là đồ thị đi qua điểm có tọa độ (0; 3).
Ngoài ra, phương trình –x2 + 2x + 3 = 0 có hai nghiệm phân biệt x1 = 3 và x2 = –1 nên đồ thị hàm số cắt trục hoành tại hai điểm phân biệt có tọa độ (3; 0) và (–1; 0).
Ta vẽ được đồ thị sau:
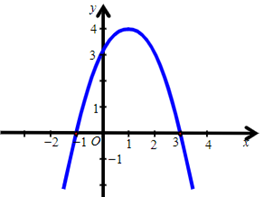
Vậy ta chọn phương án A.
Cách 2:
• Xét hàm số y = –x2 + 2x + 3 có a = –1, b = 2, c = 3.
Vì a = –1 < 0 nên đồ thị có bề lõm quay xuống dưới.
Do đó ta loại phương án C.
• Đỉnh S có tọa độ: \({x_S} = - \frac{b}{{2a}} = - \frac{2}{{2.\left( { - 1} \right)}} = 1\) và \({y_S} = - \frac{\Delta }{{4a}} = - \frac{{16}}{{4.\left( { - 1} \right)}} = 4\).
Suy ra tọa độ đỉnh S(1; 4).
Do đó ta loại phương án B và D.
Vậy ta chọn phương án A.
