Dạng 4: Xét sự biến thiên của hàm số bậc hai có đáp án
-
1927 lượt thi
-
12 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Hướng dẫn giải:
Xét hàm số y = –x2 + 4x + 5 có a = –1 < 0, b = 4, c = 5
Ta có: \(\frac{{ - b}}{{2a}} = \frac{{ - 4}}{{2.( - 1)}} = 2\); \( - \frac{\Delta }{{4a}} = - \frac{{{b^2} - 4ac}}{{4a}} = - \frac{{{{\left( { - 4} \right)}^2} - 4.( - 1).5}}{{4.( - 1)}} = 9\).
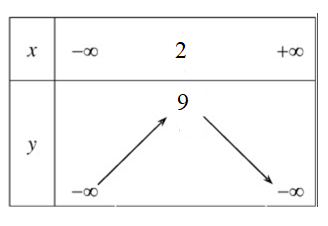
Do đó, hàm số đồng biến trên khoảng (–∞; 2), nghịch biến trên khoảng (2; +∞).
Bảng biến thiên:
Câu 2:
Hướng dẫn giải:
Xét hàm số y = 2x2 + 2x + 1 có a = 2 > 0, b = 2, c = 1.
Ta có: \(\frac{{ - b}}{{2a}} = \frac{{ - 2}}{{2.2}} = \frac{{ - 1}}{2}\); \(\frac{{ - \Delta }}{{4a}} = - \frac{{{b^2} - 4ac}}{{4a}} = - \frac{{{2^2} - 4.2.1}}{{4.2}} = \frac{1}{2}\).
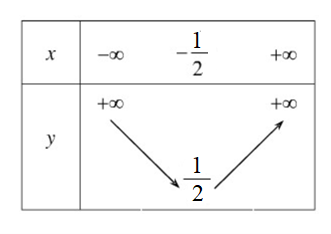
Do đó, hàm số nghịch biến trên khoảng \(\left( { - \infty ;\frac{{ - 1}}{2}} \right)\), đồng biến trên khoảng \(\left( {\frac{{ - 1}}{2}; + \infty } \right)\).
Bảng biến thiên:
Câu 3:
Hàm số y = x2 – 4x + 5 đồng biến trên khoảng:
Hướng dẫn giải:
Đáp án đúng là: A.
Xét hàm số y = x2 – 4x + 5 có a = 1 > 0, b = – 4, c = 5.
Ta có: \(\frac{{ - b}}{{2a}} = \frac{{ - ( - 4)}}{{2.1}} = 2\)
Do đó, hàm số đồng biến trên khoảng (2; +∞)
Câu 4:
Hàm số y = –3x2 + 6x + 1 đồng biến trên khoảng:
Hướng dẫn giải:
Đáp án đúng là: C.
Xét hàm số y = –3x2 + 6x + 1 có a = –3 < 0, b = 6, c = 1.
Ta có: \(\frac{{ - b}}{{2a}} = \frac{{ - 6}}{{2.( - 3)}} = 1\).
Do đó, hàm số đồng biến trên khoảng (–∞; 1).
Câu 5:
Hàm số y = –x2 + 2x – 2 nghịch biến trên khoảng:
Hướng dẫn giải:
Đáp án đúng là: D.
Xét hàm số y = –x2 + 2x – 2 có a = –1 < 0, b = 2, c = –2
Ta có: \(\frac{{ - b}}{{2a}} = \frac{{ - 2}}{{2.( - 1)}} = 1\)
Do đó, hàm số nghịch biến trên khoảng (1; +∞).
Câu 6:
Hàm số y = 4x2 – 24x – 6 nghịch biến trên khoảng:
Hướng dẫn giải:
Đáp án đúng là: A.
Xét hàm số y = 4x2 – 24x – 6 có a = 4 > 0, b = –24, c = –6.
Ta có: \(\frac{{ - b}}{{2a}} = \frac{{ - ( - 24)}}{{2.4}} = 3\).
Do đó, hàm số nghịch biến trên khoảng (–∞; 3).
Câu 7:
Cho hàm số y = x2 – 4x – 6. Khẳng định nào sau đây là đúng ?
Hướng dẫn giải:
Đáp án đúng là: C.
Xét hàm số y = x2 – 4x – 6 có a = 1 > 0, b = –4, c = –6
Ta có: \(\frac{{ - b}}{{2a}} = \frac{{ - ( - 4)}}{{2.1}} = 2\).
Do đó, hàm số nghịch biến trên khoảng (–∞; 2) và đồng biến trên khoảng (2; + ∞).
Câu 8:
Cho hàm số y = –x2 + 8x – 3. Khẳng định nào sau đây là đúng ?
Hướng dẫn giải:
Đáp án đúng là: B.
Xét hàm số y = –x2 + 8x – 3 có a = –1 < 0, b = 8, c = –3
Ta có: \(\frac{{ - b}}{{2a}} = \frac{{ - 8}}{{2.( - 1)}} = 4\)
Do đó, hàm số đồng biến trên khoảng (–∞; 4) và nghịch biến trên (4; +∞).
Câu 9:
Cho hàm số y = –x2 + 4x – 3. Khẳng định nào sau đây là đúng ?
Hướng dẫn giải:
Đáp án đúng là: A.
Xét hàm số y = –x2 + 4x – 3 có a = –1 < 0, b = 4, c = –3
Ta có: \(\frac{{ - b}}{{2a}} = \frac{{ - 4}}{{2.( - 1)}} = 2\)
Do đó, hàm số đồng biến trên khoảng (–∞; 2) và nghịch biến trên khoảng (2; +∞).
Câu 10:
Cho hàm số y = x2 + 6x – 5. Khẳng định nào sau đây là đúng ?
Hướng dẫn giải:
Đáp án đúng là: B.
Xét hàm số y = x2 + 6x – 5 có a = 1 > 0, b = 6, c = –5
Ta có: \(\frac{{ - b}}{{2a}} = \frac{{ - 6}}{{2.1}} = - 3\).
Do đó, hàm số nghịch biến trên khoảng (–∞; –3) và đồng biến trên khoảng (–3; +∞).
Câu 11:
Hướng dẫn giải:
Đáp án đúng là: D.
Xét hàm số y = –x2 + 4x – 3 có a = –1 < 0, b = 4, c = –3
Ta có: \(\frac{{ - b}}{{2a}} = \frac{{ - 4}}{{2.( - 1)}} = 2\); \(\frac{{ - \Delta }}{{4a}} = - \frac{{{b^2} - 4ac}}{{4a}} = - \frac{{{4^2} - 4.( - 1).( - 3)}}{{4.( - 1)}} = 1\).
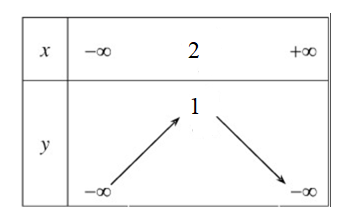
Do đó, hàm số đồng biến trên khoảng (–∞; 2), nghịch biến trên khoảng (2; +∞).
Bảng biến thiên:
Câu 12:
Đâu là bảng biến thiên của hàm số y = x2 + 6x – 5 ?
Hướng dẫn giải:
Đáp án đúng là: C.
Xét hàm số y = x2 + 6x – 5 có a = 1 > 0, b = 6, c = –5
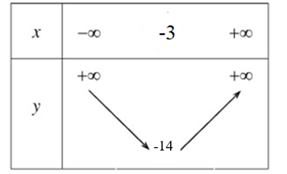
Ta có: \(\frac{{ - b}}{{2a}} = \frac{{ - 6}}{{2.1}} = - 3\); \(\frac{{ - \Delta }}{{4a}} = - \frac{{{b^2} - 4ac}}{{4a}} = - \frac{{{6^2} - 4.1.( - 5)}}{{4.1}} = - 14\).
Do đó, hàm số nghịch biến trên khoảng (–∞; –3), đồng biến trên khoảng (–3; +∞)
Bảng biến thiên: