Trắc nghiệm Toán 10 CTST Bài 2. Tập hợp có đáp án (Thông hiểu)
-
762 lượt thi
-
8 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Hướng dẫn giải
Đáp án đúng là: D
Phương án A đúng vì tập rỗng là tập con của mọi tập hợp.
Phương án B đúng vì 1 là phần tử của A nên ta kí hiệu là 1 ∈ A.
Phương án C đúng vì {1; 2} là một tập hợp, các phần tử của tập hợp này đều thuộc tập hợp A nên tập hợp {1; 2} là tập con của tập hợp A, khi đó ta kí hiệu {1; 2} ⊂ A.
Phương án D sai kí hiệu. Sửa lại: 2 ∈ A.
Vậy ta chọn phương án D.
Câu 2:
Hướng dẫn giải
Đáp án đúng là: D
Ta có:
⦁ F ⊂ G nên phương án A sai.
⦁ G ⊂ K nên phương án B sai.
⦁ Giả sử E = {1; 2}, F = {1; 2; 3}, G = {1; 2; 3; 4}.
Ta thấy trong trường hợp trên, ta có E ⊂ F, F ⊂ G nhưng F ⊄ E vì 3 ∈ F nhưng 3 ∉ E.
Do đó phương án C không đúng trong mọi trường hợp.
⦁ Ta có quan hệ bao hàm: E ⊂ F, F ⊂ G và G ⊂ K.
Ta biểu diễn mối quan hệ giữa bốn tập hợp trên biểu đồ Ven như hình bên:
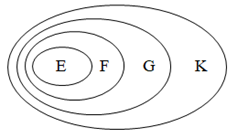
Quan sát biểu đồ Ven, ta thấy E ⊂ K.
Do đó phương án D đúng.
Vậy ta chọn phương án D.
Câu 3:
Cho tập hợp H = {1; 2; 3; 4; x; y}. Xét các mệnh đề sau đây:
(I): “3 ∈ H”;
(II): “{3; 4} ∈ H”;
(III): “{x, 3, y} ∈ H”.
Trong các mệnh đề trên, mệnh đề nào đúng?
Hướng dẫn giải
Đáp án đúng là: A
⦁ Ta thấy 3 thuộc tập hợp A, ta kí hiệu là 3 ∈ A.
Do đó mệnh đề (I) đúng.
⦁ Vì kí hiệu “{3; 4}” là kí hiệu tập hợp nên mệnh đề (II) sai.
Do phần tử 3 và 4 đều thuộc tập hợp A nên ta có thể sửa lại kí hiệu là: {3; 4} ⊂ H.
⦁ Giải thích tương tự như mệnh đề (II), ta có mệnh đề (III) sai.
Vậy chỉ có mệnh đề (I) đúng.
Do đó ta chọn phương án A.
Câu 4:
Hướng dẫn giải
Đáp án đúng là: B
⦁ Ta sử dụng kí hiệu “∈” để biểu diễn một phần tử thuộc tập hợp.
Vì kí hiệu “a” là kí hiệu của phần tử, kí hiệu [a; b] là kí hiệu của tập hợp nên để biểu diễn a là phần tử thuộc tập hợp [a; b], ta kí hiệu là a ∈ [a; b].
Do đó kí hiệu ở phương án A sai.
⦁ Ta sử dụng kí hiệu “⊂” để biểu diễn một tập hợp là tập con của một tập hợp khác.
Vì kí hiệu {a} và [a; b] đều là kí hiệu của tập hợp và phần tử a thuộc tập hợp [a; b] nên ta kí hiệu là {a} ⊂ [a; b].
Do đó kí hiệu ở phương án B đúng.
⦁ Giải thích tương tự như phương án B, ta thu được phương án C sai.
Sửa lại: {a} ⊂ [a; b].
⦁ Vì phần tử a không thuộc tập hợp (a; b] nên kí hiệu ở phương án D sai.
Sửa lại: a ∉ (a; b].
Vậy ta chọn phương án B.
Câu 5:
Cho tập hợp A = {x; y; z} và B = {x; y; z; t; u}. Tập hợp X nào trong các tập X dưới đây thỏa mãn A ⊂ X ⊂ B?
Hướng dẫn giải
Đáp án đúng là: B
Tập A là tập con của tập B khi mọi phần tử của tập hợp A đều thuộc tập hợp B.
Ta thấy tập hợp A gồm 3 phần tử là: x; y; z.
Tập hợp B gồm 5 phần tử là: x; y; z; t; u.
Trong 4 phương án A, B, C, D, ta thấy tập X ở phương án A và B đều chứa cả 3 phần tử x; y; z, còn phương án C, D không chứa cả 3 phần tử x; y; z.
Nên ta loại phương án C, D.
Ta thấy tập X ở phương án A có phần tử v ∉ B.
Do đó tập X ở phương án A không phải tập con của tập B.
Ta thấy tập X ở phương án B có 4 phần tử là x; y; z; t đều thuộc tập B.
Do đó tập X ở phương án B là tập con của tập hợp B.
Vậy ta chọn đáp án B.
Câu 6:
Hướng dẫn giải
Đáp án đúng là: B
⦁ Các phần tử của tập hợp ở phương án A là: {0; 1; 2; 3; 4; 5}.
Ta thấy phần tử 0 ∉ H.
Do đó tập hợp ở phương án A khác tập H.
⦁ Các phần tử của tập hợp ở phương án B là: {1; 2; 3; 4; 5} = H.
Do đó phương án B đúng.
⦁ Ta thấy phần tử –1 thuộc tập hợp ở đáp án C, D.
Nhưng –1 ∉ H.
Do đó tập hợp ở phương án C, D khác tập H.
Vậy ta chọn phương án B.
Câu 7:
Cho tập hợp P = {1; 3} và tập hợp Q = {3; x}. Giá trị của x để P = Q là:
Hướng dẫn giải
Đáp án đúng là: A
Ta thấy tập hợp P và Q đều có phần tử 3.
Tập P còn có phần tử 1.
Do đó để P = Q thì Q cần có thêm phần tử 1.
Nghĩa là, x = 1.
Vậy ta chọn phương án A.
Câu 8:
Viết tập hợp D gồm các chữ cái có trong từ “TOKYO”.
Hướng dẫn giải
Đáp án đúng là: B
Các chữ cái trong từ “TOKYO” là: T; O; K; Y; O.
Do mỗi phần tử chỉ được liệt kê một lần nên ta có: T; O; K; Y.
Vậy tập hợp D ={T; O; K; Y}.
Do các phần tử có thể được viết theo thứ tự tùy ý.
Nên ta chỉ cần chọn tập hợp D ở phương án đã bao gồm đủ cả 4 phần tử T; O; K; Y.
Ta thấy đáp án B thỏa mãn yêu cầu.
Vậy ta chọn phương án B.
