10 câu hỏi trắc nghiệm thuộc Dạng 2: Tìm hiệu của hai vectơ có đáp án

Trắc nghiệm Toán 10 CTST Bài 2: Tìm tổng của hai hay nhiều vectơ có đáp án

Dạng 2: Tìm hiệu của hai vectơ có đáp án

900 lượt thi
10 câu hỏi
45 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Cho 4 điểm A, B, C, D. Khẳng định nào sau đây là đúng ?

A. $\vec{A B} - \vec{D C} = \vec{A C} - \vec{D B}$

B. $\vec{A B} + \vec{C D} = \vec{A D} + \vec{B C}$

C. $\vec{A B} - \vec{D C} = \vec{A D} - \vec{B C}$

D. $\vec{A B} + \vec{C D} = \vec{D A} - \vec{C B}$

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C.

Ta có: $\vec{A B} - \vec{D C} - (\vec{A D} - \vec{B C}) = \vec{A B} - \vec{D C} - \vec{A D} + \vec{B C}$

$= \vec{A B} + \vec{C D} + \vec{D A} + \vec{B C} = (\vec{A B} + \vec{B C}) + (\vec{C D} + \vec{D A})$

$= \vec{A C} + \vec{C A} = \vec{0}$

Vậy

$\vec{A B} - \vec{D C} - (\vec{A D} - \vec{B C}) = \vec{0} \Leftrightarrow \vec{A B} - \vec{D C} = \vec{A D} - \vec{B C}$

Câu 2:

Cho 4 điểm bất kì A, B, C, O. Đẳng thức nào sau đây đúng ?

A. $\vec{O A} = \vec{O B} - \vec{B A}$

B. $\vec{A B} = \vec{O B} + \vec{O A}$

C. $\vec{A B} = \vec{A C} + \vec{B C}$

D. $\vec{O A} = \vec{C A} - \vec{C O}$

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: D.

Ta có:

$\vec{C A} - \vec{C O} = \vec{C A} + \vec{O C} = \vec{O C} + \vec{C A} = \vec{O A}$ .

Câu 3:

Cho hai điểm phân biệt A, B. Gọi I là trung điểm của đoạn thẳng AB. Khẳng định nào sau đây là đúng ?

A. $\vec{I A} - \vec{I B} = \vec{0}$

B. $\vec{A I} - \vec{B I} = \vec{0}$

C. $\vec{I A} - \vec{B I} = \vec{0}$

D. $\vec{I A} + \vec{A B} = \vec{0}$

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C.

Ta có: $\vec{I A} - \vec{B I} = \vec{I A} + \vec{I B}$

Mà do I là trung điểm của AB nên $\vec{I B} = - \vec{I A} = \vec{A I}$

Do đó: $\vec{I A} - \vec{B I} = \vec{I A} + \vec{I B} = \vec{I A} + \vec{A I} = \vec{I I} = \vec{0}$

Câu 4:

Cho ba điểm phân biệt A, B, C. Đẳng thức nào sau đây là đúng ?

A. $\vec{A B} - \vec{B C} = \vec{C A}$

B. $\vec{A B} + \vec{C A} = \vec{B C}$

C. $\vec{C A} - \vec{B A} = \vec{C B}$

D. $\vec{A B} + \vec{A C} = \vec{B C}$

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C.

Ta có: $\vec{C A} - \vec{B A} = \vec{C A} + \vec{A B} = \vec{C B}$ .

Câu 5:

Cho hình bình hành ABCD tâm O. Khẳng định nào sau đây là sai ?

A. $\vec{B D} = \vec{D C} - \vec{B C}$

B. $\vec{B D} = \vec{C D} - \vec{C B}$

C. $\vec{B D} = \vec{B C} + \vec{C D}$

D. $\vec{A C} = \vec{A B} + \vec{A D}$

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A.

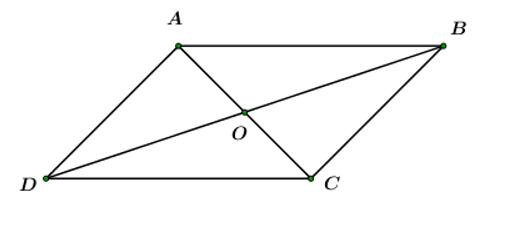
Cho hình bình hành ABCD tâm O. Khẳng định nào sau đây là sai ? (ảnh 1)

Ta có: $\vec{D C} - \vec{B C} = \vec{D C} + \vec{C B} = \vec{D B}$

Vậy $\vec{D B} = \vec{D C} - \vec{B C}$ . Do đó A sai.

Ta có: $\vec{C D} - \vec{C B} = \vec{B D}$ nên B đúng.

Theo quy tắc 3 điểm ta có: $\vec{B D} = \vec{B C} + \vec{C D}$ nên C đúng.

Theo quy tắc hình bình hành ta có: $\vec{A C} = \vec{A B} + \vec{A D}$ nên D đúng.

Câu 6:

Cho 4 điểm bất kì A, B, C, D. Khẳng định nào sau đây là đúng ?

A. $\vec{O A} = \vec{C A} + \vec{C O}$

B. $\vec{B C} - \vec{A C} + \vec{A B} = \vec{0}$

C. $\vec{B A} = \vec{O B} - \vec{O A}$

D. $\vec{O A} = \vec{O B} - \vec{B A}$

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B.

Ta có:

$\vec{B C} - \vec{A C} + \vec{A B} = \vec{B C} + \vec{C A} + \vec{A B}$

$= (\vec{B C} + \vec{C A}) + \vec{A B}$

$= \vec{B A} + \vec{A B} = \vec{B B} = \vec{0}$ .

Câu 7:

Cho hình vuông ABCD tâm O. Khi đó, $\vec{O A} - \vec{O B} = ?$

A. $\vec{C D}$

B. $\vec{A B}$

C. $\vec{A C}$

D. $\vec{B D}$

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A.

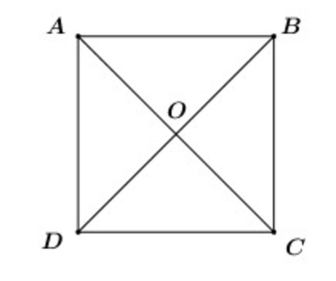
Cho hình vuông ABCD tâm O. Khi đó, vecto OA-OB=? (ảnh 1)

Xét 3 điểm A, O, B có: $\vec{O A} - \vec{O B} = \vec{B A}$

Do ABCD là hình vuông nên ta có: $\vec{B A} = \vec{C D}$

Vậy $\vec{O A} - \vec{O B} = \vec{C D}$ .

Câu 8:

Cho hình vuông ABCD. Tính $\vec{A B} - \vec{A C} + \vec{B D}$

A. $\vec{C D}$

B. $\vec{A B}$

C. $\vec{A D}$

D. $\vec{B D}$

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A.

Ta có: $\vec{A B} - \vec{A C} + \vec{B D} = \vec{A B} + \vec{C A} + \vec{B D}$

$= (\vec{C A} + \vec{A B}) + \vec{B D} = \vec{C B} + \vec{B D} = \vec{C D}$ .

Câu 9:

Cho 4 điểm A, B, C, D phân biệt. Khi đó, $\vec{A D} - \vec{C D} + \vec{C B} - \vec{D B} = ?$

A. $\vec{0}$

B. $\vec{A D}$

C. $\vec{C D}$

D. $\vec{A C}$

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B.

Ta có: $\vec{A D} - \vec{C D} + \vec{C B} - \vec{D B} = \vec{A D} + \vec{D C} + \vec{C B} + \vec{B D}$

$= (\vec{A D} + \vec{D C}) + (\vec{C B} + \vec{B D}) = \vec{A C} + \vec{C D} = \vec{A D}$ .

Câu 10:

Cho hình bình hành ABCD với giao điểm hai đường chéo là I. Khi đó:

A. $\vec{A B} - \vec{A I} = \vec{B I}$

B. $\vec{A B} - \vec{D A} = \vec{B D}$

C. $\vec{A B} - \vec{D C} = \vec{0}$

D. $\vec{A B} - \vec{D B} = \vec{0}$

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C.

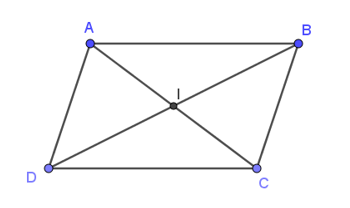
Cho hình bình hành ABCD với giao điểm hai đường chéo là I. Khi đó: (ảnh 1)

+) Ta có: $\vec{A B} - \vec{A I} = \vec{I B} \neq \vec{B I}$ nên A sai.

+) $\vec{A B} - \vec{D A} = \vec{A B} + \vec{A D} = \vec{A C} \neq \vec{B D}$ (theo quy tắc hình bình hành) nên B sai.

+) Ta có: $\vec{A B} - \vec{D C} = \vec{A B} + \vec{C D}$

Mà $\vec{B A} = \vec{C D}$ (do ABCD là hình bình hành)

Vậy $\vec{A B} - \vec{D C} = \vec{A B} + \vec{C D} = \vec{A B} + \vec{B A} = \vec{A A} = \vec{0}$ . Nên C đúng.

+) Ta có: $\vec{A B} - \vec{D B} = \vec{A B} + \vec{B D} = \vec{A D} \neq \vec{0}$ . Vậy D sai.

Bắt đầu thi ngay

CHỌN BỘ SÁCH BẠN MUỐN XEM

Trắc nghiệm Toán 10 CTST Bài 2: Tìm tổng của hai hay nhiều vectơ có đáp án

Dạng 2: Tìm hiệu của hai vectơ có đáp án

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương