100 câu trắc nghiệm Mệnh đề - Tập hợp nâng cao (P4)
-
13685 lượt thi
-
20 câu hỏi
-
20 phút
Danh sách câu hỏi
Câu 1:
Gọi Bn là tập hợp các bội số của n trong N. Tập hợp B2 ∩ B3 là :
Đáp án: D
B2 là tập hợp các số nguyên chia hết cho 2.
B3 là tập hợp các số nguyên chia hết cho 3.
B2 ∩ B3 là một tập hợp các số nguyên vừa thuộc B2, vừa thuộc B3 nghĩa là các phần tử này vừa chia hết cho 2 và vừa chia hết cho 3.
B2 ∩ B3 là một tập hợp các phần tử chia hết cho 6 . Do đó B2 ∩ B3 = B6
Câu 2:
Gọi Bn là tập hợp các bội số của n trong N. Tập hợp B2 ∩ B4 là
B2 là tập hợp các số tự nhiên chia hết cho 2.
B4 là tập hợp các số tự nhiên chia hết cho 4.
Vì các số tự nhiên chia hết cho 4 thì chia hết cho 2, nhưng ngược lại các số tự nhiên chia hết cho 2 chưa chắc chia hết cho 4 nên ta có: .
Khi đó: .
Chọn B.
Câu 3:
Gọi Bn là tập hợp các bội số của n trong N. Tập hợp B3 ∪ B6 là:
Đáp án: D
B3 là tập hợp các số nguyên chia hết cho 3.
B6 là tập hợp các số nguyên chia hết cho 6.
Các số chia hết cho 6 chắc chắn phải chia hết cho 3, ngược lại các số chia hết cho 3 thì chưa chắc chia hết cho 6.
Do đó B6 ⊂ B3 => B3 ∪ B6 = B3
Câu 4:
Cho X = {n ∈ N*|n là bội số của 6 và 4}, Y = {n ∈ N*| n là bội số của 12} các mệnh đề sau mệnh đề nào sai:
Đáp án: D
Vì bội số của 6 và 4 cũng là bội số của 12 nên X = {n ∈ N* | n là bội số của 6 và 4} = {n ∈ N*| n là bội số của 12}.
Nghĩa là, X = Y => X ⊂ Y , Y ⊂ X. Vậy D là đáp án sai
Câu 5:
Cho các tập hợp M = {x ∈ N: x là bội số của 2}; N = {x ∈ N: x là bội số của 6}; P = {x ∈ N: x là ước số của 2}; Q = {x ∈ N: x là ước số của 6}. Mệnh đề nào sau đây đúng?
Đáp án: C
M là tập hợp các số nguyên chia hết cho 2. N là tập hợp các số nguyên chia hết cho 6. Các số chia hết cho 6 chắc chắn phải chia hết cho 2, ngược lại các số chia hết cho 2 thì chưa chắc chia hết cho 6. Do đó N ⊂ M => M ∩ N = N
=> A sai, C đúng.
P = {1; 2}; Q = {1; 2; 3; 6}. Do đó P ⊂ Q => P ∩ Q = P => B, D sai.
Câu 6:
Cho các tập hợp M = {x ∈ N: x là bội số của 10}; N = {x ∈ N: x là bội số của 2}; P = {x ∈ N: x là ước số của 15}; Q = {x ∈ N: x là ước số của 30}. Mệnh đề nào sau đây đúng?
Đáp án: A
M là tập hợp các số nguyên chia hết cho 10. N là tập hợp các số nguyên chia hết cho 2.
Các số chia hết cho 10 chắc chắn phải chia hết cho 2, ngược lại các số chia hết cho 2 thì chưa chắc chia hết cho 10. Do đó M ⊂ N => M ∩ N= M => A đúng, C sai.
P = {1; 3; 5; 15}; Q = {1; 2; 3; 5; 6; 10; 15; 30}.
Do đó P ⊂ Q => P ∩ Q = P => B, D sai
Câu 7:
Cho H = tập hợp các hình bình hành, V = tập hợp các hình vuông, N = tập hợp các hình chữ nhật, T = tập hợp các hình thoi. Mệnh đề sai là:
Đáp án: C
Hình vuông là hình thoi đặc biệt có 4 góc vuông nên V ⊂ T đúng.
Hình vuông là hình chữ nhật đặc biệt có 4 cạnh bằng nhau nên V ⊂ N đúng.
Hình thoi là hình bình hành đặc biệt có 4 cạnh bằng nhau nên H ⊂ T sai.
Hình chữ nhật là hình bình hành đặc biệt có 4 góc vuông nên N ⊂ H đúng.
Câu 8:
Cho A ={1;2}, B ={1;2;3;4;5}. Số tập hợp X sao cho (A ∪ X) = B là:
Đáp án: D
X={1;2;3;4;5}; X={2;3;4;5}; X={1;3;4;5}; X={3;4;5}.
Câu 9:
Cho A = {x ∈ Z | x2 < 4}; B = { x ∈ Z | (5x - 3x2)(x2 - 2x - 3)= 0}. Số phần tử của tập hợp (A∪B) \ (A ∩ B) là:
Đáp án: C
A = {0;-1;1}; B = {0;-1;3}
A ∪ B = {0;-1;1;3}; A ∩ B = {0;-1}
(A ∪ B) \ (A ∩ B) = {1;3} => có 2 phần tử.
Câu 10:
Cho số thực a < 0. Điều kiện cần và đủ để (-∞; 9a] ∩ [; +∞) ≠ ∅ là:
Để thì
(vì a < 0)
Mà a < 0 nên
Vậy
Chọn B
Câu 11:
Cho hai tập hợp E = {x ∈ R: f(x) = 0}; F = { x ∈ R: g(x) = 0}; H = {x ∈ R : f(x).g(x) = 0}. Trong các mệnh đề sau, mệnh đề đúng là:
Đáp án: A
f(x).g(x) = 0 f(x) = 0 hoặc g(x) = 0. Nghĩa là H là tập hợp bao gồm các phần tử thuộc E hoặc thuộc F hay H = E ∪ F.
Câu 12:
Cho hai tập hợp E = {x ∈ R: f(x) = 0}; F = {x ∈ R: g(x) = 0}; H = { x ∈ R: f(x)2 + g(x)2 = 0}. Trong các mệnh đề sau, mệnh đề đúng là
Đáp án: B
f(x)2 + g(x)2 = 0 ⇔ f(x) = 0 và g(x) = 0. Nghĩa là H là tập hợp bao gồm các phần tử vừa thuộc E vừa thuộc F hay H = E ∩ F
Câu 13:
Cho hai tập hợp E = {x ∈ R: f(x) = 0}; F = { x ∈ R: g(x) = 0}; H = {x ∈ R: = 0}. Trong các mệnh đề sau, mệnh đề đúng là:
Đáp án: C
f(x)/g(x) = 0 ⇔ f(x) = 0 và g(x) ≠ 0. Nghĩa là H là tập hợp bao gồm các phần tử thuộc E nhưng không thuộc F hay H = E \ F.
Câu 14:
Cho A là tập hợp các số tự nhiên chẵn không lớn hơn 10; B = {n ∈ N: n ≤ 6 } và C = {n ∈ N: 4 ≤ n ≤ 10}. Khi đó các câu đúng là:Cho A là tập hợp các số tự nhiên chẵn không lớn hơn 10; B = {n ∈ N: n ≤ 6 }
Đáp án: C
A = {0; 2; 4; 6; 8; 10}; B = {0; 1; 2; 3; 4; 5; 6}; C = {4; 5; 6; 7; 8; 9; 10}.
B ∪ C = {0; 1;2; 3;4; 5; 6; 7; 8; 9; 10}
A ∩ (B ∪ C) = {0; 2; 4; 6; 8; 10}= A.
A\B = {8; 10}; A\C = {0; 2}; B \ C = {0; 1; 2; 3}
(A \ B) ∪ (A \ C) ∪ (B \ C) = {0; 1; 2; 3; 8; 10}
Câu 15:
Cho A là tập hợp các ước nguyên dương của 24, B là tập hợp các ước nguyên dương của 18. Trong các khẳng định sau, khẳng định sai là:
Đáp án: C
A = {1; 2; 3; 4; 6; 8; 12; 24} ⇒ A có 8 phần tử ⇒ A đúng.
B = {1; 2; 3; 6; 9; 18} ⇒ B có 6 phần tử ⇒ B đúng.
A ∪ B = {1; 2; 3; 4; 6; 8; 9; 12; 18; 24} ⇒ có 10 phần tử ⇒ C sai.
B \ A = {9; 18} ⇒ có 2 phần tử ⇒ D đúng.
Câu 16:
Cho tập hợp , B là tập hợp các giá trị nguyên của tham số b để phương trình x2 - 2bx + 4 = 0 vô nghiệm. Khẳng định nào sau đây đúng?
Đáp án: B
Để phương trình vô nghiệm thì
Câu 17:
Cho các tập hợp A = {x ∈ R: x2 + 4 = 0}; B = {x ∈ R: (x2 - 4)(x2 + 1) = 0}; C = {-2; 2}; D = {x ∈ R: |x| < 2}. Khẳng định nào sau đây đúng?
Đáp án: A
Vì x2 + 4 > 0 ∀x ∈ R nên A = ∅.
(x2 - 4)(x2 + 1) = 0 ⇔ (x2 - 4) = 0 ⇔ x = ±2 nên B = {-2; 2}.
|x| < 2 ⇔ -2 < x < 2 nên D = (-2; 2).
=> A ⊂ B = C ⊂ D.
Câu 18:
Cho các tập hợp A = {x ∈ R : (x2 - 4) (x2 - 1) = 0}; B = {x ∈ R : (x2 - 4) (x2 + 1) = 0}; C = {-1; 0; 1; 2}; D = {x ∈ R : = 0}. Khẳng định nào sau đây đúng?
Đáp án: D
(x2 - 4) (x2 - 1) = 0 ⇔ x = ±2; x = ±1 nên A = {-2; -1; 1; 2}
(x2 - 4) (x2 + 1) = 0 ⇔ x2 - 4 = 0 ⇔ x = ±2 nên B = {-2; 2}
x4 - 5x2 + 4)/x = 0 ⇔ x4 - 5x2 + 4 = 0 ⇔ x = ±2; x = ±1 nên D = {-2; -1; 1; 2}
=> A = D
Câu 19:
Cho A, B, C là các tập hợp được minh họa như hình vẽ. Phần bị gạch trong hình vẽ minh họa cho tập hợp nào sau đây?
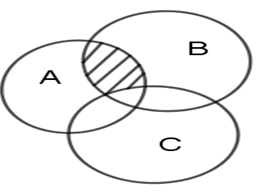
Đáp án: B
Phần bị gạch là phần thuộc (A ∩ B) nhưng không thuộc C nên phần bị gạch biểu thị cho (A ∩ B) \ C.
Câu 20:
Cho A và B là hai tập hợp con hữu hạn của tập hợp E được biểu diễn bởi biểu đồ Ven dưới đây.
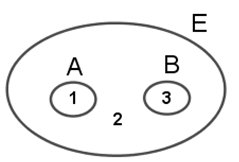
Trong các phát biểu sau, phát biểu đúng là:
Đáp án: D
A ∩ = A nên vùng 1 là tập hợp A ∩ CEB
CEA \ B = E \ (A ∪ B) nên vùng 2 là tập hợp CEA \ B.
B ∩ CEA = B nên vùng 3 là tập hợp B ∩ CEA
