Đề thi Giữa kì 1 Toán 10 có đáp án - Đề 1
-
436 lượt thi
-
28 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 10:
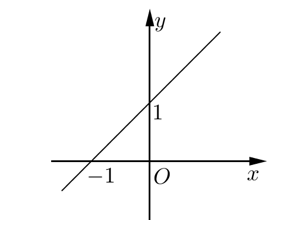
Trong mặt phẳng Oxy, biết điểm M(2; y0) thuộc đồ thị của hàm số y = 2x – 3. Giá trị của y0 bằng:
Chọn đáp án D
Câu 11:
Trong mặt phẳng Oxy đồ thị của hàm số y = x2 – 2x + 3 có trục đối xứng là đường thẳng nào dưới đây ?
Chọn đáp án A
Câu 14:
Cho I là trung điểm của đoạn thẳng AB và M là một điểm tùy ý. Mệnh đề nào dưới đây đúng?
Chọn đáp án A
Câu 15:
Cho hai tập hợp A = {1; 2; 3; 4; 5} và B = {1; 3; 5; 7}. Số phần tử của tập hợp A\B là
Chọn đáp án B
Câu 16:
Cho hai tập hợp A = [– 2; 3), B = [1; 5]. Khi đó A B là tập hợp nào dưới đây ?
Chọn đáp án B
Câu 23:
Cho tam giác ABC có AB = 6,5 cm, AC = 8,5 cm, A=185o. Tính độ dài cạnh BC (làm tròn kết quả đến hàng phần mười theo đơn vị tương ứng).
Chọn đáp án B
Câu 24:
Miền nghiệm của bất phương trình 2x – 3y > 5 là nửa mặt phẳng (không kể đường thẳng d: 2x – 3y = 5) không chứa điểm có tọa độ nào sau đây?
Chọn đáp án B
Câu 25:
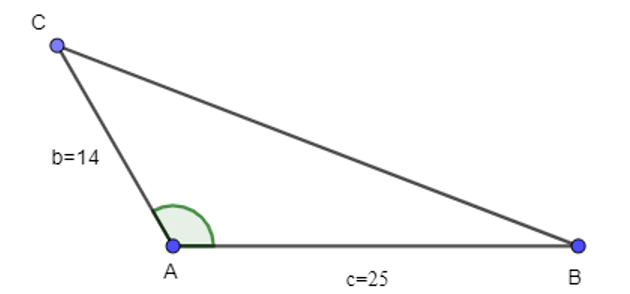
Xét ∆ABC, có:
Áp dụng định lí cosin, ta có:
BC2 = AB2 + AC2 – 2AB.AC.cosA
⇔ BC2 = 252 + 142 – 2.25.14.cos120°
⇔ BC2 = 1 171
⇔ BC ≈ 34,22.
Áp dụng hệ quả của định lí cosin, ta có:
cosB = ⇒ .
Ta có: C =
Câu 26:
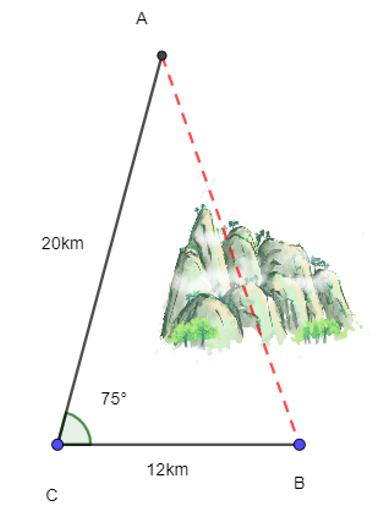
Xét tam giác ABC, có:
Áp dụng định lí cosin trong tam giác ABC, có:
AB2 = BC2 + AC2 – 2.AB.BC.cosA
⇔ AB2 = 122 + 202 – 2.12.20.cos75°
⇔ AB2 ≈ 419,77
⇔ AB ≈ 20,49 (km).
Ta có: AC + BC = 20 + 12 = 32 (km).
Vậy chiều dài tăng thêm vì không thể nối trực tiếp từ A đến B là 32 – 20,49 ≈ 11,51 km.
Câu 27:
Anh Trung có kế hoạch đầu tư 400 triệu đồng vào hai khoản X và Y. Để đạt được lợi nhuận thì khoản X phải đầu tư ít nhất 100 triệu đồng và số tiền đầu tư cho khoản Y không nhỏ hơn số tiền cho khoản X. Viết hệ bất phương trình bậc nhất hai ẩn để mô tả hai khoản đầu tư đó và biểu diễn miền nghiệm của hệ bất phương trình vừa tìm được.
Gọi x (triệu đồng) là số tiền anh Trung đầu tư vào khoản X và y (triệu đồng) là số tiền anh Trung đầu tư vào khoản Y (x, y ≥ 0).
Vì anh Trung đầu tư 400 triệu đồng vào hai khoản X và Y nên ta có x + y ≤ 400.
Để đạt được lợi nhuận thì khoản X phải đầu tư ít nhất 100 triệu đồng nên ta có x ≥ 100 và số tiền đầu tư cho khoản Y không nhỏ hơn số tiền cho X nên ta cũng có y ≥ x hay x – y ≤ 0.
Từ đó ta có hệ bất phương trình sau:
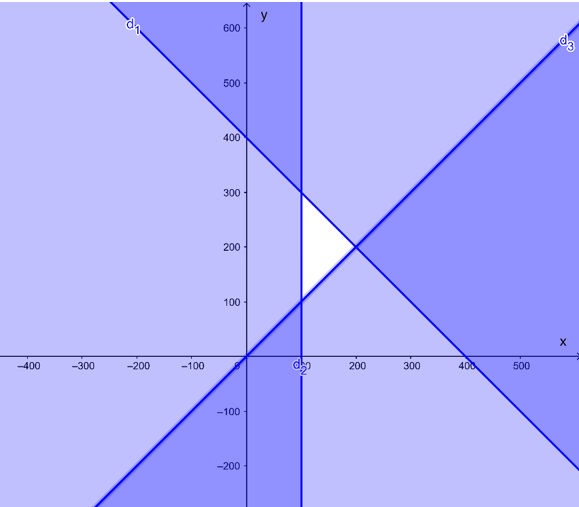
Ta vẽ bốn đường thẳng:
d1: x + y = 400 là đường thẳng đi qua hai điểm có tọa độ (400; 0) và (0; 400);
d2: x = 100 là đường thẳng song song với trục Oy và đi qua điểm có tọa độ (100; 0);
d3: x – y = 0 là đường thẳng đi qua hai điểm có tọa độ (0; 0) và (1; 1).
Ta xác định từng miền nghiệm của từng bất phương trình trong hệ, gạch đi các phần không thuộc miền nghiệm của mỗi bất phương trình.
Miền nghiệm của hệ bất phương trình là miền trong tứ giác ABCD với như hình vẽ sau:
Câu 28:
Lớp 10A có 36 học sinh, trong đó mỗi học sinh đều biết chơi ít nhất một trong hai môn thể thao đá cầu hoặc cầu lông. Biết rằng lớp 10A có 25 học sinh biết chơi đá cầu, có 20 học sinh biết chơi cầu lông. Hỏi lớp 10A có bao nhiêu học sinh biết chơi cả hai môn đá cầu và cầu lông?
Gọi A là tập hợp số học sinh biết chơi đá cầu. Khi đó |A| = 25;
B là tập hợp số học sinh biết chơi cầu lông. Khi đó |B| = 20.
Vì mỗi học sinh đều biết chơi ít nhất một trong hai môn thể thao đá cầu hoặc cầu lông nên ta có: A ∪ B là tập hợp số học sinh của lớp 10A. Khi đó |A ∪ B| = 36.
Ta có: |A ∪ B| = |A| + |B| – |A ∩ B| ⇒ |A ∩ B| = 25 + 20 – 36 = 9 (học sinh).
Vậy lớp 10A có 9 học sinh biết chơi cả hai môn đá cầu và cầu lông.