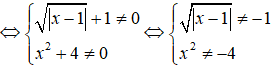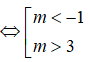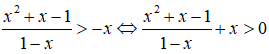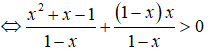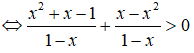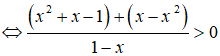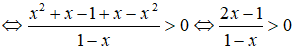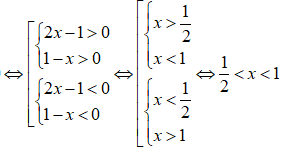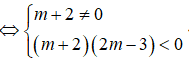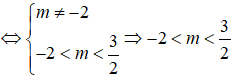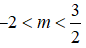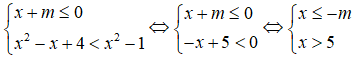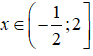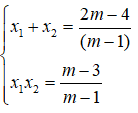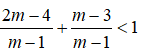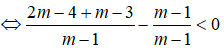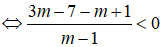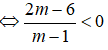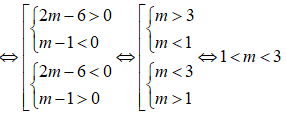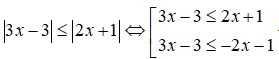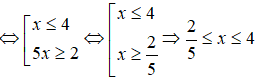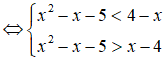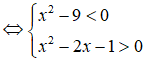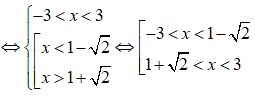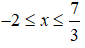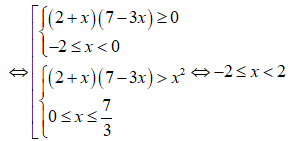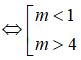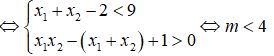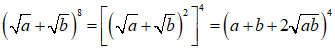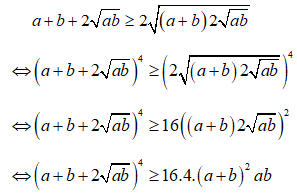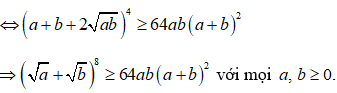15 câu hỏi trắc nghiệm thuộc Đề kiểm tra 45 phút Đại số 10 Chương 4 có đáp án (Đề 2)

Câu 1:

Phần I: Trắc nghiệm

Điều kiện xác định của bất phương trình $\frac{2 x}{\sqrt{|x - 1|} + 1} - \frac{1}{x^{2} + 4} \leq 0$ là:

A. $\{\begin{cases} x \neq 2 \\ x \geq 1 \end{cases}$

B. x $\in ℝ$

C. $\{\begin{cases} x \neq 2 \\ x \neq - 2 \end{cases}$

D. x $\geq 1$

Xem đáp án

Chọn B.

Bất phương trình xác định sau (luôn đúng)

⇒ x ∈ R.

Câu 2:

Tập nghiệm của bất phương trình 2x(2 - x) ≥ 2 - x là:

A. S = [ $\frac{1}{2}$ ; $+ \infty$ )

B. S = ( $- \infty$ ; $\frac{1}{2}$ ] $\cup$ [2; $+ \infty$ )

C. S = [0; $+ \infty$ )

D. [ $\frac{1}{2}$ ;2]

Xem đáp án

Chọn D.

Ta có:

Câu 3:

Với giá trị nào của m thì bất phương trình $m^{2}$ x + m - 1 < x vô nghiệm?

A. m = 1 và m = -1

B. m = 1

C. m = -1

D. m ∈ ∅

Xem đáp án

Chọn B.

Xét bất phương trình:

$m^{2}$ x + m - 1 < x ⇔ $m^{2}$ x - x + m - 1 < 0 ⇔ ( $m^{2}$ - 1)x < 1 - m (1)

Với m = 1, bất phương trình (1) trở thành: 0x < 0 ⇔ 0 < 0 (Vô lý) ⇒ Bất phương trình vô nghiệm.

Với m = -1 , bất phương trình (1) trở thành: 0x < 2 ⇔ 0 < 2 (luôn đúng) ⇒ Bất phương trình có vô số nghiệm.

Vậy bất phương trình $m^{2}$ x + m - 1 < x vô nghiệm khi m = 1.

Câu 4:

Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?

A. 2 $x^{2}$ + 3y > 0

B. $x^{2}$ + $y^{2}$ < 2

C. x + $y^{2}$ ≥ 0

D. x + y ≥ 0

Xem đáp án

Chọn D.

Câu 5:

Phương trình $x^{2}$ - (m + 1)x + 1 = 0 có nghiệm khi và chỉ khi

A. m > 1

B. –3 < m < 1

C. m ≤ -3 hoặc m ≥ 1

D. -3 ≤ m ≤ 1

Xem đáp án

Chọn C.

Xét phương trình: $x^{2}$ - (m + 1)x + 1 = 0

Ta có: Δ = (m + 1 $)^{2}$ - 4.1.1 = $m^{2}$ - 2m + 1 - 4 = $m^{2}$ - 2m - 3

Phương trình $x^{2}$ - (m + 1)x + 1 = 0 có nghiệm

⇔ Δ ≥ 0 ⇔ $m^{2}$ - 2m - 3 ≥ 0

Câu 6:

Tập nghiệm của bất phương trình $\frac{x^{2} + x - 1}{1 - x} > - x$ là

A. ( $\frac{1}{2}$ ;1)

B. ( $\frac{1}{2}$ ; $+ \infty$ )

C. (1; $+ \infty$ )

D. ( $- \infty$ ; $\frac{1}{2}$ ) $\cup$ (1; $+ \infty$ )

Xem đáp án

Chọn A.

Ta có:

Vậy tập nghiệm của bất phương trình là (1/2;1).

Câu 7:

Phương trình (m + 2) $x^{2}$ - 3x + 2m - 3 = 0 có hai nghiệm trái dấu khi và chỉ khi

A. m<-2

B. -2<m< $\frac{3}{2}$

C. ( $- \infty$ ; $- \frac{9}{2}$ ]

D. [ $- \frac{9}{2}$ ; $+ \infty$ )

Xem đáp án

Chọn B.

Phương trình (m + 2) $x^{2}$ - 3x + 2m - 3 = 0 có hai nghiệm trái dấu

Vậy phương trình (m + 2) $x^{2}$ - 3x + 2m - 3 = 0 có hai nghiệm trái dấu khi

Câu 8:

Cho hệ bất phương trình:

$\{\begin{cases} x + m \leq 0 \\ x^{2} - x + 4 < x^{2} - 1 \end{cases}$

Hệ bất phương trình đã cho có nghiệm khi và chỉ khi

A. m < –5

B. m > –5

C. m > 5

D. m < 5

Xem đáp án

Chọn B.

Xét hệ bất phương trình:

Để hệ bất phương trình có nghiệm thì 5 < -m ⇔ m > -5.

Câu 9:

Với x thuộc tập hợp nào dưới đây thì f(x) = x(5x + 2) - x( $x^{2}$ + 6) không dương

A. ( $- \infty$ ;1] ∪ [4; $+ \infty$ )

B. [1;4]

C. (1;4)

D. [0;1] ∪ [4; $+ \infty$ )

Xem đáp án

Chọn D.

Để f(x) = x(5x + 2) - x( $x^{2}$ + 6) không dương thì

x(5x + 2) - x(x2 + 6) ≤ 0 ⇔ x( $x^{2}$ - 5x + 4) ≥ 0

Vậy x ∈ [0;1] ∪ [4; $+ \infty$ ).

Câu 10:

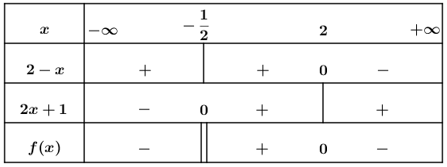
Tập nghiệm của bất phương trình $f (x) = \frac{2 - x}{2 x + 1}$

A. S = (-1/2;2)

B. S = ( $- \infty$ ;-1/2) $\cup$ (2; $+ \infty$ )

C. S = ( $- \infty$ ;-1/2) $\cup$ [2; $+ \infty$ )

D. S = (-1/2;2]

Xem đáp án

Chọn B.

Ta có :

2 - x = 0 ⇔ x = 2

2x + 1 = 0 ⇔ x = -1/2

Xét dấu f(x):

Vậy f(x) ≥ 0 khi

Câu 11:

Với giá trị nào của m thì phương trình: (m - 1) $x^{2}$ - 2(m - 2)x + m - 3 = 0 có hai nghiệm x1, x2 và x1 + x2 + x1x2 < 1?

A. 1 < m < 2

B. 1 < m < 3

C. m > 2

D. m > 2

Xem đáp án

Chọn B.

Ta có: Δ = (m - 2 $)^{2}$ - (m - 1)(m - 3) = ( $m^{2}$ - 4m + 4 ) - ( $m^{2}$ - 4m + 3) = 1 > 0

Phương trình có hai nghiệm phân biệt x1, x2.

Áp dụng hệ thức Vi-ét ta có:

Ta có:

Câu 12:

Bất phương trình : |3x - 3| ≤ |2x + 1| có tập nghiệm là

A. [4; $+ \infty$ )

B. ( $- \infty$ ; $\frac{2}{5}$ ]

C. [ $\frac{2}{5}$ ;4]

D. ( $- \infty$ ;4]

Xem đáp án

Chọn C.

Vậy tập nghiệm của bất phương trình là $[\frac{2}{5}; 4]$

Câu 13:

Phần II: Tự luận

Giải các bất phương trình:

a) $\frac{x^{2} - 2 x - 8}{(x + 1) (x^{2} - 4 x + 3)} \geq 0$

b) $|x^{2} - x - 5| < 4 - x$

c) $\sqrt{x + 2} + \sqrt{7 - 3 x} > 3$

Xem đáp án

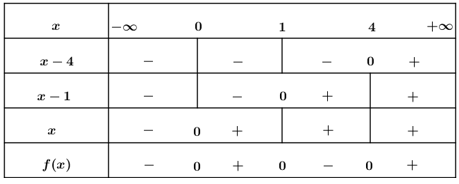
a) $\frac{x^{2} - 2 x - 8}{(x + 1) (x^{2} - 4 x + 3)} \geq 0$

Lập bảng xét dấu:

Tập nghiệm của bất phương trình là [-2;-1) ∪ (1;3) ∪ [4; $+ \infty$ )

b) | $x^{2}$ - x - 5| < 4 - x

Ta có:

| $x^{2}$ - x - 5| < 4 - x

Vậy tập nghiệm của bất phương trình là (-3;1 $- \sqrt{2}$ ) ∪ (1 $+ \sqrt{2}$ ;3).

c) $\sqrt{x + 2} + \sqrt{7 - 3 x} > 3$

Điều kiện:

Bình phương hai vế của bất phương trình ta được:

Vậy tập nghiệm của bất phương trình là [-2;2).

Câu 14:

Cho phương trình: $x^{2}$ - 2(m - 3)x + 5 - m = 0

a) Giải phương trình khi m = 1.

b) Tìm tất cả các giá trị của m để phương trình có hai nghiệm phân biệt x1, x2 thỏa mãn x1 < x2 < 1.

Xem đáp án

a) Với m = 1 phương trình trở thành:

$x^{2}$ + 4x + 4 = 0 ⇔ (x + 2 $)^{2}$ = 0 ⇔ x = -2

Vậy x = -2

b) Ta có: Δ' = $m^{2}$ - 5m + 4

Phương trình có hai nghiệm phân biệt

⇔ Δ' > 0 ⇔ $m^{2}$ - 5m + 4 > 0

Do x1 < x2 < 1

Câu 15:

Chứng minh rằng ${(\sqrt{a} + \sqrt{b})}^{8} \geq 64 a b {(a + b)}^{2}$ , với mọi a, b ≥ 0

Xem đáp án

Xét ${(\sqrt{a} + \sqrt{b})}^{8}$ với mọi a,b ≥ 0 ta có:

Áp dụng bất đẳng Cô-si cho hai số dương a + b và $2 \sqrt{a b}$ ta được:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Top 4 Đề kiểm tra 1 tiết Toán 10 Chương 4 Đại Số có đáp án

Đề kiểm tra 45 phút Đại số 10 Chương 4 có đáp án (Đề 2)

Danh sách câu hỏi

Phần I: Trắc nghiệm

Phần II: Tự luận

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương