Trắc nghiệm Toán 10 CTST Bài 1. Giá trị lượng giác của một góc từ 0° đến 180° có đáp án
Dạng 1: Xác định giá trị lượng giác của góc đặc biệt có đáp án
-
1175 lượt thi
-
13 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Hướng dẫn giải:
Lấy điểm M trên nửa đường tròn đơn vị sao cho \(\widehat {xOM} = 120^\circ \).
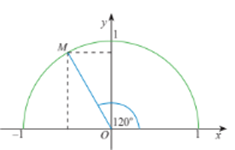 Ta có: \(\widehat {MOy} = 120^\circ - 90^\circ = 30^\circ \).
Ta có: \(\widehat {MOy} = 120^\circ - 90^\circ = 30^\circ \).
Ta tính được tọa độ điểm M: \(\left\{ \begin{array}{l}{x_0} = - \left( {OM.\sin 30^\circ } \right) = - \left( {1.\frac{1}{2}} \right) = - \frac{1}{2}\\{y_0} = OM.\cos 30^\circ = 1.\frac{{\sqrt 3 }}{2} = \frac{{\sqrt 3 }}{2}\end{array} \right.\).
Hay \(M\left( { - \frac{1}{2};\,\,\frac{{\sqrt 3 }}{2}} \right)\).
Vậy theo định nghĩa ta có:
\(\sin 120^\circ = \frac{{\sqrt 3 }}{2};\,\cos 120^\circ = - \frac{1}{2}\); \(\tan 120^\circ = - \sqrt 3 ;\,\cot 120^\circ = - \frac{{\sqrt 3 }}{3}\).
Câu 2:
Hướng dẫn giải:
Ta có sin135° = sin(180° – 45°) = sin45° = \(\frac{{\sqrt 2 }}{2}\);
cos135° = cos(180° – 45°) = – cos45° = \( - \frac{{\sqrt 2 }}{2}\);
\(\tan 135^\circ = \frac{{\sin 135^\circ }}{{\cos 135^\circ }} = \frac{{\frac{{\sqrt 2 }}{2}}}{{ - \frac{{\sqrt 2 }}{2}}} = - 1\).
Do đó cot135° = \(\frac{{cos135^\circ }}{{\sin 135^\circ }} = \frac{{ - \frac{{\sqrt 2 }}{2}}}{{\frac{{\sqrt 2 }}{2}}} = - 1\).
Câu 3:
Hướng dẫn giải:
Ta có \(\widehat F = 180^\circ - \left( {\widehat D + \widehat E} \right) = 180^\circ - 30^\circ = 150^\circ \).
Do đó sinF = sin150° = sin(180° − 30°) = sin30° = \(\frac{1}{2}\);
cosF = cos150° = cos(180° − 30°)= − cos30° = \( - \frac{{\sqrt 3 }}{2}\);
tanF = \(\frac{{\sin 150^\circ }}{{\cos 150^\circ }} = \frac{{\frac{1}{2}}}{{ - \frac{{\sqrt 3 }}{2}}} = - \frac{{\sqrt 3 }}{3}\);
cotF = \(\frac{{cos150^\circ }}{{\sin 150^\circ }} = \frac{{ - \frac{{\sqrt 3 }}{2}}}{{\frac{1}{2}}}\)= \( - \sqrt 3 \).
Câu 4:
Hướng dẫn giải:
Đáp án đúng là: D.
Ta có sin120° = sin(180° – 60°) = sin60°\( = \frac{{\sqrt 3 }}{2}\).
cos120° = cos(180° – 60° ) = – cos60° \( = - \frac{1}{2}\).
Do đó \(\tan 120^\circ = \frac{{\sin 120^\circ }}{{\cos 120^\circ }} = - \sqrt 3 \);
\(\cot 120^\circ = - \frac{1}{{\sqrt 3 }}\).
Câu 5:
Hướng dẫn giải:
Đáp án đúng là: A.
Ta có sin60° = \(\frac{{\sqrt 3 }}{2}\); cos60° = \(\frac{1}{2}\); tan60° =\(\sqrt 3 \); cot60° =\(\frac{1}{{\sqrt 3 }}\).
Câu 6:
Hướng dẫn giải:
Đáp án đúng là: B.
Ta có: tan135° = – tan(180° – 45°) = – 1.
Câu 7:
Hướng dẫn giải:
Đáp án đúng là: D.
Ta có:
sin 0° = 0;
cos 90° = 0;
cos 0° = 1;
sin 90° = 1 nên đáp án D sai.
Câu 8:
Hướng dẫn giải:
Đáp án đúng là: A.
Ta có sin A = sin 45° = \(\frac{{\sqrt 2 }}{2}\), suy ra đáp án sai là A.
cos A = cos 45° = \(\frac{{\sqrt 2 }}{2}\);
tan A = tan 45° = 1;
cot A = cot 45° = 1.
Vậy các đáp án B, C, D đúng.
Câu 9:
Hướng dẫn giải:
Đáp án đúng là: D.
Ta có sin (180° – α) = sin α = \(\frac{1}{2}\).
Do đó \(\frac{a}{b} = \frac{1}{2}\), mà \(\frac{a}{b}\) là phân số tối giản nên a = 1, b = 2.
Vậy a + b = 1 + 2 = 3.
Câu 10:
Hướng dẫn giải:
Đáp án đúng là: C.
Ta có \(\widehat B = 60^\circ \) nên sin B = sin 60° = \(\frac{{\sqrt 3 }}{2}\); cos B = cos 60° = \(\frac{1}{2}\) nên A, B sai.
Lại có \[\widehat C = 180^\circ - \left( {\widehat A + \widehat B} \right) = 180^\circ - \left( {90^\circ + 60^\circ } \right) = 30^\circ \] (áp dụng định lí tổng ba góc trong tam giác).
Do đó sin C = sin 30° = \(\frac{1}{2}\); cos C = cos 30° = \(\frac{{\sqrt 3 }}{2}\).
Vậy C đúng, D sai.
Câu 11:
Hướng dẫn giải:
Đáp án đúng là: A.
Vì tam giác ABC cân tại A nên \(\widehat B = \widehat C = \frac{{180^\circ - \widehat A}}{2} = \frac{{180^\circ - 120^\circ }}{2} = 30^\circ \).
Do đó \(\sin B = \sin 30^\circ = \frac{1}{2}\).
Câu 12:
Hướng dẫn giải:
Đáp án đúng là: B.
Ta có: cos90° = 0 nên A = 0.
Câu 13:
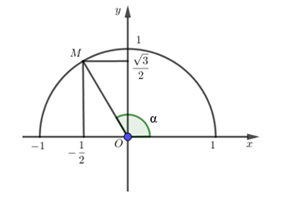
Cho góc α như hình vẽ, xác định giá trị của tan α.
Hướng dẫn giải:
Đáp án đúng là: D.
Từ hình vẽ ta thấy điểm M có tọa độ \(\left( { - \frac{1}{2};\,\,\frac{{\sqrt 3 }}{2}} \right)\).
Do đó: \(\tan \alpha = \frac{{\frac{{\sqrt 3 }}{2}}}{{ - \frac{1}{2}}} = - \sqrt 3 \).
