Dạng 2: Tìm tập xác định, tập giá trị của hàm số có đáp án
-
881 lượt thi
-
14 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Hàm số v = f(t) được cho bởi bảng như sau:

Tìm tập xác định của hàm số này.
Hướng dẫn giải:
Xét hàm số v = f(t) ta có: t là biến số, v là hàm số của t.
Tập xác định của hàm số là tập giá trị của t nên ta có: D = {0,5; 1; 1,2; 1,8; 2,5}.
Câu 2:
Hướng dẫn giải:
Xét hàm số v = f(t) ta có: t là biến số, v là hàm số của t.
Tập giá trị của hàm số là tập giá trị của v nên ta có: T = {1,5; 3; 0; 5,4; 7,5}.
Câu 3:
Cho hàm số \(f(x) = \sqrt {2x + 7} \).
Tìm tập xác định của hàm số.
Hướng dẫn giải:
Xét hàm số: \(f(x) = \sqrt {2x + 7} \).
Tập xác định của hàm số là tập giá trị của x sao cho \(f(x) = \sqrt {2x + 7} \) có nghĩa.
Điều kiện xác định của hàm số là:
2x + 7 ≥ 0 ⇔ 2x ≥ –7 ⇔ \(x \ge \frac{{ - 7}}{2}\)
Vậy tập xác định của hàm số là: \(D = \left[ { - \frac{7}{2}; + \infty } \right)\).
Câu 4:
Cho hàm số \(f(x) = \sqrt {2x + 7} \).
Hướng dẫn giải:
Xét hàm số: \(f(x) = \sqrt {2x + 7} \).
Với mọi giá trị x thuộc \(D = \left[ { - \frac{7}{2}; + \infty } \right)\), ta thấy: \(f(x) = \sqrt {2x + 7} \) ≥ 0
Do đó, tập giá trị của hàm số \(f(x) = \sqrt {2x + 7} \) là T = [0; +∞).
Câu 5:
Hướng dẫn giải:
Đáp án đúng là: C.
Xét hàm số f(x) = x – 2 ta thấy f(x) = x – 2 luôn có nghĩa với mọi giá trị thực của x. Do đó, tập xác định của hàm số là D = ℝ.
Câu 6:
Cho hàm số cho bởi bảng sau:
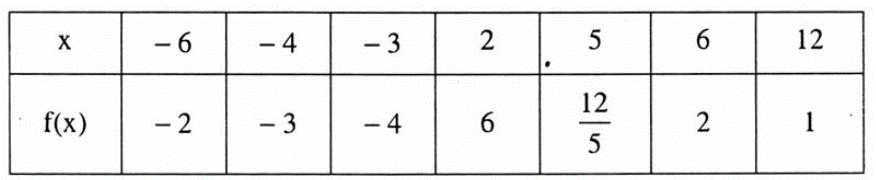
Tập xác định của hàm số f(x) là:
Hướng dẫn giải:
Đáp án đúng là: B.
Dựa vào bảng trên, ta thấy tập xác định của hàm số f(x) là tập giá trị của x, do đó ta có:
D = {–6; –4; –3; 2; 5; 6; 12}
Câu 7:
Cho hàm số cho bởi bảng sau:
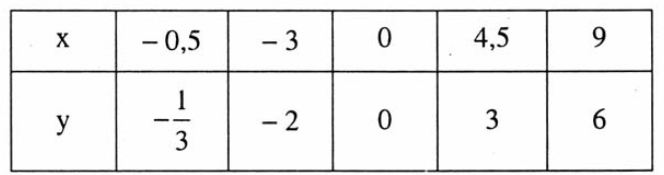
Tập xác định của hàm số y là:
Hướng dẫn giải:
Đáp án đúng là: A
Dựa vào bảng trên, ta thấy tập xác định của hàm số y là tập giá trị của x, do đó ta có:
D = {–0,5; –3; 0; 4,5; 9}.
Câu 8:
Hướng dẫn giải:
Đáp án đúng là: D.
Điều kiện xác định của hàm số \(f(x) = \frac{1}{{x - 1}}\) là: x – 1 ≠ 0 ⇔ x ≠ 1.
Vậy tập xác định của hàm số \(f(x) = \frac{1}{{x - 1}}\) là: D = ℝ \ {1}.
Câu 9:
Hướng dẫn giải:
Đáp án đúng là: B.
Điều kiện xác định của hàm số \(f(x) = \frac{{x - 3}}{{x + 2}}\) là: x + 2 ≠ 0 ⇔ x ≠ –2.
Vậy tập xác định của hàm số \(f(x) = \frac{{x - 3}}{{x + 2}}\) là: D = ℝ \ {–2}.
Câu 10:
Tập xác định của hàm số \(f(x) = \frac{{x + 3}}{{{x^2} + 1}}\) là:
Hướng dẫn giải:
Đáp án đúng là: D.
Điều kiện xác định của hàm số \(f(x) = \frac{{x + 3}}{{{x^2} + 1}}\) là: x2 + 1 ≠ 0 ⇔ x2 ≠ –1
Mà x2 ≥ 0 với mọi số thực x, do đó, x2 ≠ –1 với mọi số thực x.
Vậy tập xác định của hàm số \(f(x) = \frac{{x + 3}}{{{x^2} + 1}}\) là D = ℝ.
Câu 11:
Hướng dẫn giải:
Đáp án đúng là: A.
Điều kiện xác định của hàm số \(f(x) = \sqrt {2x - 4} \) là: 2x – 4 ≥ 0 ⇔ 2x ≥ 4 ⇔x ≥ 2
Vậy tập xác định của hàm số \(f(x) = \sqrt {2x - 4} \) là D = [2; +∞).
Câu 12:
Hàm số \(f(x) = \frac{3}{{\sqrt {x - 4} }}\) có tập xác định là:
Hướng dẫn giải:
Đáp án đúng là: C.
Điều kiện xác định của hàm số \(f(x) = \frac{3}{{\sqrt {x - 4} }}\) là: x – 4 > 0 ⇔ x > 4
Vậy tập xác định của hàm số \(f(x) = \frac{3}{{\sqrt {x - 4} }}\) là D = (4; +∞).
Câu 13:
Tập giá trị của hàm số: \(f(x) = \frac{{2022}}{{\sqrt {2x - 2} }}\) là:
Hướng dẫn giải:
Đáp án đúng là: C.
Điều kiện xác định của hàm số \(f(x) = \frac{{2022}}{{\sqrt {2x - 2} }}\) là: 2x – 2 > 0 ⇔ 2x > 2 ⇔ x > 1.
Vậy tập xác định của hàm số \(f(x) = \frac{{2022}}{{\sqrt {2x - 2} }}\) là D = (1; +∞).
Với mọi giá trị x thuộc D = (1; +∞) ta dễ thấy: 2022 > 0 và \(\sqrt {2x - 2} \) > 0
Do đó, ta có: \(f(x) = \frac{{2022}}{{\sqrt {2x - 2} }}\) > 0 với mọi x thuộc D = (1; +∞).
Vậy tập giá trị của hàm số \(f(x) = \frac{{2022}}{{\sqrt {2x - 2} }}\) là T = (0; +∞).
Câu 14:
Hướng dẫn giải:
Đáp án đúng là: D.
Điều kiện xác định của hàm số \(f(x) = \frac{{x - 4}}{{x + 4}}\) là: x + 4 ≠ 0 ⇔ x ≠ –4 .
Vậy tập xác định của hàm số \(f(x) = \frac{{x - 4}}{{x + 4}}\) là D = ℝ\{–4}.
Với mọi giá trị x thuộc D = ℝ\{–4} ta dễ thấy: x – 4 ∈ ℝ và x + 4 ≠ 0
Do đó, ta có: \(f(x) = \frac{{x - 4}}{{x + 4}}\)∈ ℝ với mọi x thuộc D = ℝ\{–4}.
Vậy tập giá trị của hàm số \(f(x) = \frac{{x - 4}}{{x + 4}}\) là T = ℝ.
