Trắc nghiệm Toán 10 CTST Bài tập cuối chương 2 có đáp án (Vận dụng)
-
538 lượt thi
-
5 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Tất cả các giá trị thực của tham số m để bất phương trình 3x + my − 7 ≥ 0 có miền nghiệm chứa điểm A(\(\sqrt 2 \); 1) là:
Hướng dẫn giải
Đáp án đúng là: D
Do điểm A(\(\sqrt 2 \); 1) thuộc miền nghiệm của bất phương trình, thay x = \(\sqrt 2 \) và y = 1 vào bất phương trình ta được:
\(3\sqrt 2 + m - 7 \ge 0 \Leftrightarrow m \ge 7 - 3\sqrt 2 \)
Vậy với \(m \in \left[ {7 - 3\sqrt 2 ; + \infty } \right)\) thì bất phương trình 3x + my − 7 ≥ 0 có miền nghiệm chứa điểm A(\(\sqrt 2 \); 1).
Ta chọn phương án D.
Câu 2:
Hướng dẫn giải
Đáp án đúng là: B
Ta có: 2x − 3(y − x) > 4 ⇔ 2x – 3y + 3x – 4 > 0 ⇔ 5x – 3y – 4 > 0.
Do điểm A(1 − m; m) không thuộc miền nghiệm của bất phương trình nên thay tọa độ điểm A vào bất phương trình trên không thoả mãn hay điểm A thuộc miền nghiệm của bất phương trình 5x – 3y – 4 ≤ 0.
Khi đó ta có: 5(1 – m) – 3m – 4 ≤ 0
⇔ 5 – 5m – 3m – 4 ≥ 0
⇔ –8m ≥ –1
⇔ m ≤ \(\frac{1}{8}\)
Ta chọn phương án B.
Câu 3:
Cho hệ bất phương trình \(\left\{ \begin{array}{l}0 \le y \le 4\\x \ge 0\\x - y - 1 \le 0\\x + 2y - 10 \le 0\end{array} \right..\) Gọi điểm có toạ độ (x; y) thuộc miền nghiệm của hệ bất phương trình sao cho F(x; y) = x + 2y đạt giá trị lớn nhất. Số điểm thoả mãn là:
Hướng dẫn giải
Đáp án đúng là: C
Ta có: \[\left\{ {\begin{array}{*{20}{c}}{0 \le y \le 4}\\{x \ge 0}\\{x - y - 1 \le 0}\\{x + 2y - 10 \le 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}\begin{array}{l}y \ge 0\\y \le 4\end{array}\\{x \ge 0}\\{x - y - 1 \le 0}\\{x + 2y - 10 \le 0}\end{array}} \right.\]
Trên mặt phẳng Oxy:
• Biểu diễn miền nghiệm của bất phương trình: y ≥ 0.
Miền nghiệm của bất phương trình y ≥ 0 là nửa mặt phẳng (kể cả đường thẳng d1: y = 0) chứa điểm (0; 1).
• Biểu diễn miền nghiệm của bất phương trình: y ≤ 4.
Miền nghiệm của bất phương trình y ≤ 4 là nửa mặt phẳng (kể cả đường thẳng d2: y = 4) chứa điểm (0; 1).
• Biểu diễn miền nghiệm của bất phương trình: x ≥ 0.
Miền nghiệm của bất phương trình x ≥ 0 là nửa mặt phẳng (kể cả đường thẳng d3: x = 0) chứa điểm (1; 0).
• Biểu diễn miền nghiệm của bất phương trình: x – y – 1 ≤ 0.
Vẽ đường thẳng d4: x – y – 1 = 0 đi qua hai điểm (0; –1) và (1; 0).
Xét điểm O(0; 0) ∉ d1, ta có: 0 – 0 – 1 = –1 < 0 nên miền nghiệm của bất phương trình x – y – 1 ≥ 0 là nửa mặt phẳng (kể cả bờ d4) chứa điểm O(0; 0).
• Biểu diễn miền nghiệm của bất phương trình: x + 2y – 10 ≤ 0.
Vẽ đường thẳng d5: x + 2y – 10 = 0 đi qua hai điểm (0; 5) và (10; 0).
Xét điểm O(0; 0) ∉ d1, ta có: 0 + 2.0 – 10 = –10 < 0 nên miền nghiệm của bất phương trình x + 2y – 10 ≤ 0 là nửa mặt phẳng (kể cả bờ d5) chứa điểm O(0; 0).
Miền không gạch chéo (kể cả bờ d1, d2, d3, d4 và d5) là giao của các miền nghiệm và cũng là phần biểu diễn miền nghiệm của hệ bất phương trình đã cho.
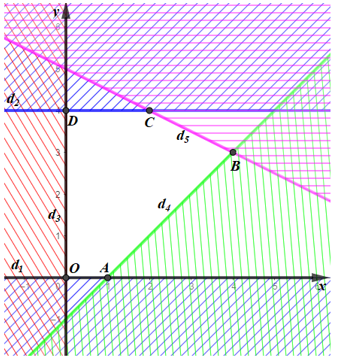
Miền nghiệm của hệ bất phương trình là miền ngũ giác OABCD với O(0; 0), A(1; 0), B(4; 3), C(2; 4) và D(0; 4).
Xét biểu thức F(x; y) = x + 2y:
Tại O(0; 0): F = 0 + 2.0 = 0;
Tại A(1; 0): F = 1 + 2.0 = 1;
Tại B(4; 3): F = 4 + 2.3 = 10;
Tại C(2; 4): F = 2 + 2.4 = 10;
Tại D(0; 4): F = 0 + 2.4 = 8.
F(x; y) đạt giá trị lớn nhất bằng 10 tại hai điểm B(4; 3) và C(2; 4).
Vậy có 2 điểm thỏa mãn yêu cầu đề bài. Ta chọn phương án C.
Câu 4:
Hướng dẫn giải
Đáp án đúng là: B
Trên mặt phẳng Oxy:
• Biểu diễn miền nghiệm của bất phương trình: x ≥ 0.
Miền nghiệm của bất phương trình x ≥ 0 là nửa mặt phẳng (kể cả đường thẳng d1: x = 0) chứa điểm (1; 0).
• Biểu diễn miền nghiệm của bất phương trình: x – y – 1 ≤ 0.
Vẽ đường thẳng d2: x – y – 1 = 0 đi qua hai điểm (0; –1) và (1; 0).
Xét điểm O(0; 0) ∉ d2, ta có: 0 – 0 – 1 = –1 < 0 nên miền nghiệm của bất phương trình x – y – 1 ≥ 0 là nửa mặt phẳng (kể cả bờ d2) chứa điểm O(0; 0).
• Biểu diễn miền nghiệm của bất phương trình: x + 2y – 10 ≤ 0.
Vẽ đường thẳng d3: x + 2y – 10 = 0 đi qua hai điểm (0; 5) và (10; 0).
Xét điểm O(0; 0) ∉ d1, ta có: 0 + 2.0 – 10 = –10 < 0 nên miền nghiệm của bất phương trình x + 2y – 10 ≤ 0 là nửa mặt phẳng (kể cả bờ d3) chứa điểm O(0; 0).
Miền không gạch chéo (kể cả bờ d1, d2, d3) là giao của các miền nghiệm và cũng là phần biểu diễn miền nghiệm của hệ bất phương trình đã cho.
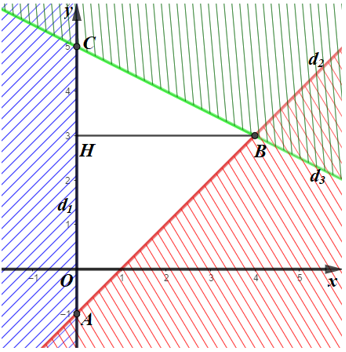
Miền nghiệm của hệ bất phương trình là miền tam giác ABC với A(–1; 0), B(4; 3) và C(0; 5).
Gọi BH là đường cao kẻ từ B đến AC.
Khi đó BH = |xB| = 4.
CA = CO + OA = |yC| + |yA| = 5 + 1 = 6.
Diện tích của tam giác ABC là:
S = \(\frac{1}{2}\) BH.CA = \(\frac{1}{2}\) .4.6 = 12 (đơn vị diện tích).
Vậy ta chọn phương án B.
Câu 5:
Hướng dẫn giải
Đáp án đúng là: B
Chi phí cho 30 giây quảng cáo trên sóng phát thanh là 5 000 000 đồng, trên sóng truyền hình là 15 000 000 đồng nên chi phí cho 1 phút quảng cáo trên sóng phát thanh là 10 000 000 đồng, trên sóng truyền hình là 30 000 000 đồng.
Gọi thời lượng công ty đặt quảng cáo trên sóng phát thanh là x (phút), trên truyền hình là y (phút).
Chi phí cho quảng cáo trên sóng phát thanh là: 10 000 000x (đồng).
Chi phí cho quảng cáo trên truyền hình là: 30 000 000y (đồng).
Tổng chi phí cho việc quảng cáo là: 10 000 000x + 30 000 000y (đồng).
Do công ty dự định chi tối đa 20 000 000 đồng cho quảng cáo nên ta có:
10 000 000x + 30 000 000y ≤ 20 000 000
Hay x + 3y ≤ 2 Û x + 3y – 2 ≤ 0.
Đổi 10 giây = \(\frac{1}{6}\) phút, 30 giây = \(\frac{1}{2}\) phút.
Sóng phát thanh chỉ nhận phát các chương trình quảng cáo có thời lượng ít nhất là 30 giây và nhiều dài nhất 2 phút nên ta có:
\(\frac{1}{2}\) ≤ x ≤ 2 \[ \Leftrightarrow \left\{ \begin{array}{l}x \ge \frac{1}{2}\\x \le 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x - \frac{1}{2} \ge 0\\x - 2 \le 0\end{array} \right.\]
Đài truyền hình chỉ nhận các chương trình quảng cáo có thời lượng ít nhất là 10 giây và nhiều nhất là 30 giây nên ta có:
\(\frac{1}{6}\) ≤ y ≤ \(\frac{1}{2}\) \( \Leftrightarrow \left\{ \begin{array}{l}y \ge \frac{1}{6}\\y \le \frac{1}{2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y - \frac{1}{6} \ge 0\\y - \frac{1}{2} \le 0\end{array} \right.\)
Hiệu quả chung của quảng cáo là: x + 6y.
Bài toán trở thành: Xác định x, y sao cho F(x; y) = x + 6y đạt giá trị lớn nhất với:
\[\left\{ \begin{array}{l}x - \frac{1}{2} \ge 0\\x - 2 \le 0\\y - \frac{1}{6} \ge 0\\y - \frac{1}{2} \le 0\\x + 3y - 2 \le 0\end{array} \right.\]
Biểu diễn miền nghiệm của hệ bất phương trình trên mặt phẳng Oxy:
• Miền nghiệm của bất phương trình x – \(\frac{1}{2}\) ≥ 0 là nửa mặt phẳng (kể cả bờ d1: x – \(\frac{1}{2}\) = 0) không chứa điểm O(0; 0).
• Miền nghiệm của bất phương trình x – 2 ≤ 0 là nửa mặt phẳng (kể cả bờ d2: x – 2 = 0) chứa điểm O(0; 0).
• Miền nghiệm của bất phương trình y – \(\frac{1}{6}\) ≥ 0 là nửa mặt phẳng (kể cả bờ d3: y – \(\frac{1}{6}\)= 0) không chứa điểm O(0; 0).
• Miền nghiệm của bất phương trình y – \(\frac{1}{2}\) ≤ 0 là nửa mặt phẳng (kể cả bờ d4: y – \(\frac{1}{2}\) = 0) chứa điểm O(0; 0).
• Miền nghiệm của bất phương trình x + 3y – 2 ≤ 0 là nửa mặt phẳng (kể cả bờ d5: x + 3y – 2 = 0) chứa điểm O(0; 0).
Miền không gạch chéo (kể cả bờ d1, d2, d3, d4 và d5) là giao của các miền nghiệm và cũng là phần biểu diễn miền nghiệm của hệ bất phương trình đã cho.
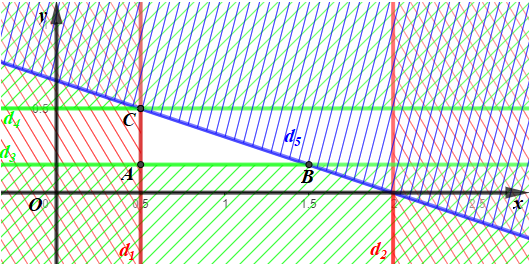
Miền nghiệm của hệ bất phương trình là miền tam giác ABC với A\(\left( {\frac{1}{2};\frac{1}{6}} \right),\) B\(\left( {\frac{3}{2};\frac{1}{6}} \right)\) và C\(\left( {\frac{1}{2};\frac{1}{2}} \right).\)
Xét F(x; y) = x + 6y ta có:
Tại A\(\left( {\frac{1}{2};\frac{1}{6}} \right):\) F = \(\frac{1}{2} + 6.\frac{1}{6} = 1,5;\)
Tại B\(\left( {\frac{3}{2};\frac{1}{6}} \right):\) F = \(\frac{3}{2} + 6.\frac{1}{6} = 2,5;\)
Tại C\(\left( {\frac{1}{2};\frac{1}{2}} \right):\) F = \(\frac{1}{2} + 6.\frac{1}{2} = 3,5.\)
Khi đó F(x; y) đạt giá trị lớn nhất bằng 3,5 tại C\(\left( {\frac{1}{2};\frac{1}{2}} \right).\)
Tức là công ty đó cần đặt thời lượng trên đài phát thanh \(\frac{1}{2}\) phút = 30 giây và trên đài truyền hình \(\frac{1}{2}\) phút = 30 giây để đạt hiệu quả nhất.
Vậy ta chọn phương án B.
