25 câu hỏi trắc nghiệm thuộc 100 câu trắc nghiệm Tích vô hướng của hai vectơ nâng cao (P2)

Câu 1:

Cho hai điểm A(2; 2); B( 5; -2) . Tìm M trên tia Ox sao cho $\hat{A M B} = 90^{o}$

A. M(1; 4)

B. (0; 6)

C. M(1;0) hoặc M(6; 0)

D. M(0;1)

Xem đáp án

Chọn C.

Gọi M(x; 0).

Khi đó .

Theo đàu bài suy ra AM và MB vuông góc với nhau

ta có

nên : (x - 2) (x - 5) – 4 = 0 hay x²- 7x + 6 = 0 $(x - 1) (x - 6) = 0 \Leftrightarrow [\begin{matrix} x - 1 = 0 \\ x - 6 = 0 \end{matrix} \Leftrightarrow [\begin{matrix} x = 1 \\ x = 6 \end{matrix}$

suy ra: x = 1; y = 0 hoặc x = 6; y = 0.

Câu 2:

Trong mặt phẳng tọa độ Oxy cho hai vectơ $\vec{u} = \vec{i} + 2 \vec{j}; \vec{v} = k \vec{i} + 2 \vec{j}$ . Tìm k để vectơ $\vec{u}$ vuông góc với vectơ $\vec{v}$

A. k = 2

B. k = 8

C. k = -4

D. k = 4

Xem đáp án

Chọn C.

Từ giả thiết suy ra

Để 2 vecto trê vuông góc với nhau khi và chỉ khi:

nên 1.k + 2.2 = 0

Do đó: k = -4

Câu 3:

Cho tam giác ABC có BC = a; CA = b; AB = c. Tính $\vec{A B} . \vec{A C}$

A. ½.( c²+ b²- a²)

B. c²+ b²- a²

C. a²- b²- c²

D. a²+ b²+ c²

Xem đáp án

Chọn A.

Ta có

Câu 4:

Cho tam giác ABC có BC = a; CA = b; AB = c. M là trung điểm của BC, D là chân đường phân giác trong góc A. Tính ${\vec{A M}}^{2}$

A.

B.

C.

D.

Xem đáp án

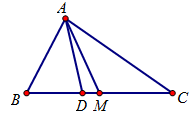
Chọn A.

+ Vì M là trung điểm của BC nên

Suy ra

Theo câu trên ta có nên

Câu 5:

Cho các vectơ $\vec{a}; \vec{b}$ có độ dài bằng 1 và thoả mãn điều kiện $2 \vec{a} - 3 \vec{b} = \sqrt{7}$ . Tính cos $(\vec{a}; \vec{b})$

A. 1

B. 0

C. 0,5

D. Tất cả sai

Xem đáp án

Chọn C.

Do nên

Hay nên

Mà nên

Câu 6:

Cho các véctơ $\vec{a}; \vec{b}$ có độ dài bằng 1 và góc tạo bởi hai vectơ bằng 60⁰. Xác định cosin góc giữa hai vectơ $\vec{u} = \vec{a} + 2 \vec{b}; \vec{v} = \vec{a} - \vec{b}$

A. -1/2

B. -1/4

C. -1/6

D. 0

Xem đáp án

Chọn C.

Ta có:

Mặt khác : nên

nên

Suy ra

Câu 7:

Giá trị của E = sin36⁰.cos6⁰ - sin126⁰.cos84⁰ là

A. 0,5

C. 1

D. -1

Xem đáp án

Chọn A.

Ta có:

E = sin36⁰.cos6⁰ - sin126⁰.cos84⁰= sin36⁰.cos6⁰- sin(90⁰+ 36⁰).cos(90⁰ - 6⁰)

E = sin36⁰.cos6⁰- cos36⁰.sin6⁰= sin30⁰= 0,5

Câu 8:

Giá trị của biểu thức A = sin²41⁰+ sin²45⁰+ sin²49⁰+ sin²45⁰ là

A. 3.

B. 4.

C. 1.

D. 2.

Xem đáp án

Chọn D.

Ta có:

A = sin²41⁰+ sin²45⁰+ sin²49⁰+ sin²45⁰= (sin²41⁰+ sin²49⁰)+( sin²45⁰+ sin²45⁰)

A = (sin²41⁰+ cos²49⁰) + ( sin²45⁰+ cos²45⁰) = 1 + 1 = 2.

Câu 9:

Cho biết cosα = -2/3 . Tính giá trị của biểu thức ? $E = \frac{c o t α + 3 \tan α}{2 c o t α + \tan α}$ ?

A. $- \frac{19}{13}$

B. $\frac{19}{13}$

C. $\frac{25}{13}$

D. - $\frac{19}{3}$

Xem đáp án

Chọn B.

Nhân cả tử và mẫu với tanα ta được

Câu 10:

Cho biết cotα = 5. Tính giá trị của E = 2 cos²α + 5sinα.cosα + 1?

Xem đáp án

Chọn D.

Ta có:

Câu 11:

Cho hình vuông ABCD cạnh bằng 1. Trên cạnh AB lấy điểm M sao cho BM = 1, trên cạnh CD lấy điểm N sao cho DN = 1 và P là trung điểm BC. Tính cosMNP?

Xem đáp án

Chọn C.

Ta có

Suy ra

Mặt khác

Câu 12:

Cho tứ giác ABCD. Gọi M, N lần lượt là trung điểm của DA, BC. Tính góc giữa hai đường thẳng AB và CD biết AB = CD = 2a; $M N = a \sqrt{3}$ .

A. 30⁰

B. 45⁰

C. 60⁰

D. 90⁰

Xem đáp án

Chọn C.

Ta có: suy ra

Do đó

Câu 13:

Tính A = sin²2⁰ + sin²4⁰+ sin² 6⁰+… + sin²84⁰+ sin²86⁰+ sin²88⁰.

A. 20

B. 22

C. 24

D. 23

Xem đáp án

Chọn B.

Ta có: A = sin²2⁰ + sin²4⁰+ sin² 6⁰+…+ sin²84⁰+ sin²86⁰+ sin²88⁰

A = ( sin²2⁰ + sin² 88⁰) + ( sin² 4⁰+ sin²86⁰) +...+ (sin²44⁰+ sin²46⁰)

A = ( sin²2⁰ + cos²2⁰) + ( sin² 4⁰+…+ cos²4⁰) +...+ ( sin²44⁰+ cos²44⁰) ( do 2 góc phụ nhau sin góc này bằng cos góc kia).

A = 1 + 1 + 1 + ... + 1 = 22

Câu 14:

Biết sina+ cosa = $\sqrt{2}$ . Hỏi giá trị của sin⁴a + cos⁴a bằng bao nhiêu?

A. 1

B. 0,5

C. -1

D. 0

Xem đáp án

Chọn B.

Ta có:

Nên (sina + cosa)²=2 hay sin²a + cos²a + 2 sina.cosa = 2

Suy ra sina.cosa = ½.

Khi đó: sin⁴a + cos⁴a = (sin²a + cos²a)²- 2sin²a.cos²a = 1 - 2.(1/2)²= ½.

Câu 15:

Biểu thức A = 3(sin⁴x + cos⁴x) - 2 (sin⁶x + cos⁶x) có giá trị bằng:

A. 1

B. 2

C. -1

D. 0

Xem đáp án

Chọn A.

Ta có:

+ sin⁴x + cos⁴x = (sin²x + cos²x)²- 2sin²x.cos²x = 1 - 2sin²x.cos²x.

+ sin⁴x + cos⁴x = 1 - 3sin²x.cos²x.

Do đó

A = 3(1 - 2sin²x^.cos²x) - 2(1 - 3sin²x.cos²x) = 1.

Câu 16:

Biểu thức: A = cos⁴x + cos²x sin²x + sin²x có giá trị bằng

A. 1

B. 2

C. 3

D. 4

Xem đáp án

Chọn A.

Từ giả thiết suy ra:

A = (cos⁴x + cos²x sin²x) + sin²x = cos²x(sin²x + cos²x ) + sin²x

A = cos²x.1 + sin²x = 1

Câu 17:

Biểu thức B = sin²x.tan²x – tan²x + sin² x có giá trị bằng

A. -2

B. -1

C. 0

D. 1

Xem đáp án

Chọn C.

Từ giả thiết ta suy ra:

B = tan²x (sin²x - 1) + sin² x = -tan²x.cos²x + sin²x

Câu 18:

Cho cotα = 1/3. Giá trị của biểu thức là:

A. -11

B. 11

C. 12

D. 13

Xem đáp án

Chọn D.

Ta có: cosα = sinα.cotα nên từ giả thiết suy ra:

Câu 19:

Cho biết cosα = -2/3. Giá trị của biểu thức $E = \frac{c o t α - 3 \tan α}{2 c o t α - \tan α}$ bằng bao nhiêu?

A . $\frac{- 25}{3}$

B. $\frac{11}{3}$

C. - $\frac{11}{3}$

D. $\frac{16}{3}$

Xem đáp án

Chọn C.

Nhân cả tử và mẫu với tanα và chú ý tanα.cotα = 1 ta được:

Câu 20:

Cho tanα + cotα = m. Tìm m để tan²α + cot²α = 7.

A. m = 3

B. m = 6

C. m = -3

D. m = ± 3

Xem đáp án

Chọn D.

Theo giả thiết tan²α + cot²α = 7.

Nên ( tanα + cotα) ²= tan²α + cot²α + 2tanα.cotα = 7 + 2 = 9

Suy ra: tanα + cotα = 3 hoặc tanα + cotα = -3

Suy ra: m = 3 hoặc m = -3.

Câu 21:

Biểu thức (cota + tana)²bằng

A.

B. cot²a + tan²a.

C .

D. cot²a.tan²a + 2.

Xem đáp án

Chọn C.

Ta có: cota + tana) ²= cot²a + 2.cota.tana + tan²a

= (cot²a + 1) + (tan²a + 1)

Câu 22:

Đơn giản biểu thức $E = c o t x + \frac{\sin x}{1 + \cos x}$ ta được

A. sinx

B.

C.

D. tanx

Xem đáp án

Chọn C.

Ta có:

Câu 23:

Rút gọn biểu thức sau $A = \frac{c o t^{2} x - \cos^{2} x}{c o t^{2} x} + \frac{\sin x . \cos x}{c o t x}$

A. A = 1

B. A = -1

C. A = -2

D. A = 2

Xem đáp án

Chọn A.

Ta có:

Câu 24:

Cho hình vuông ABCD tâm O. Hỏi mệnh đề nào sau đây sai?

A.

B.

C.

D.

Xem đáp án

Chọn C.

+ Phương án A: ABCD là hình vuông nên OA và OB vuông góc với nhau

suy ra $\vec{O A} . \vec{O B} = 0$ loại A.

+ Phương án B: OA và OC vuông góc với nhau nên $\vec{O A} . \vec{O C} = 0$ và $\frac{1}{2} \vec{O A} . \vec{A C} = 0$

suy ra $\vec{O A} . \vec{O C} = \frac{1}{2} \vec{O A} . \vec{A C} = 0$ loại B.

+ Phương án C: $\vec{A B} . \vec{A C} = A B . A C . \cos 45 ° = A B . A B . \sqrt{2} . \frac{\sqrt{2}}{2} = A B^{2}$

Do $\vec{A B}, \vec{C D}$ là hai vecto ngược hướng nên $(\vec{A B}; \vec{C D}) = 180 °$

suy ra :

Câu 25:

Trong mặt phẳng tọa độ Oxy cho các điểm A(1;2); B(-2; -4) và C(0;1); D(-1; 3/2). Mệnh đề nào sau đây đúng ?

A. $\vec{A B} c ù n g p h ư ơ n g v ớ i \vec{C D}$

B.

C.

D.

Xem đáp án

Chọn C.

Ta có và

suy ra

Vậy 2 vecto đó vuông góc với nhau.

CHỌN BỘ SÁCH BẠN MUỐN XEM

100 câu trắc nghiệm Tích vô hướng của hai vectơ nâng cao

100 câu trắc nghiệm Tích vô hướng của hai vectơ nâng cao (P2)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương