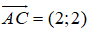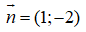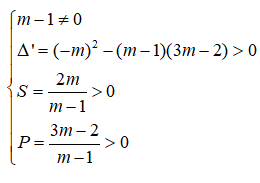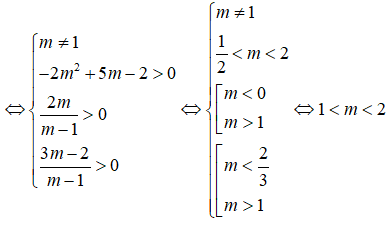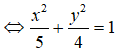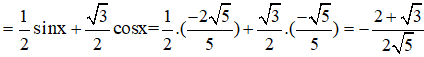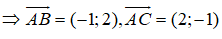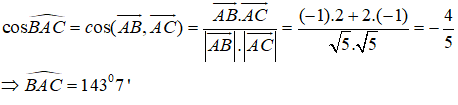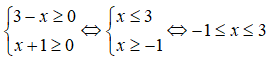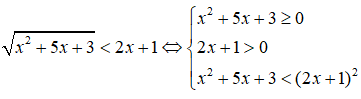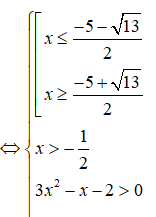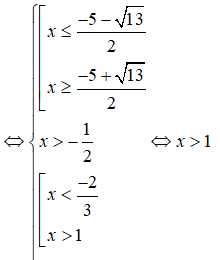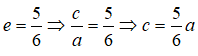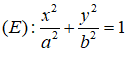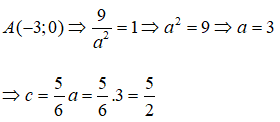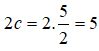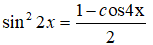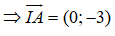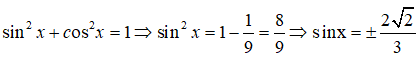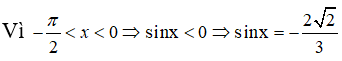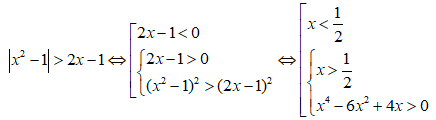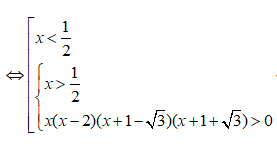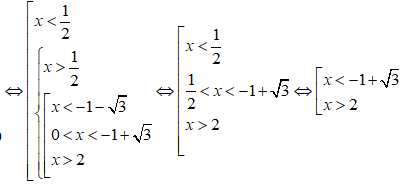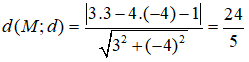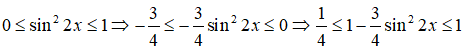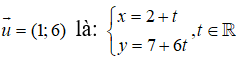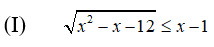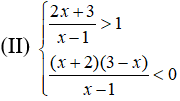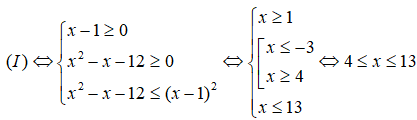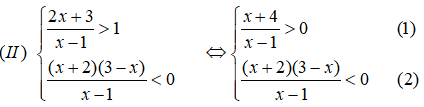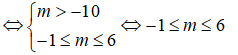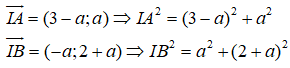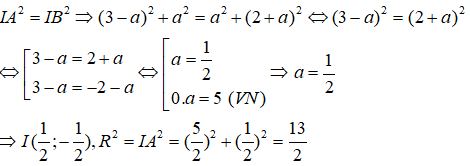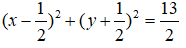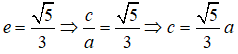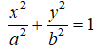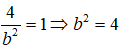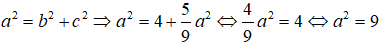23 câu hỏi trắc nghiệm thuộc Đề thi Học kì 2 Toán 10 có đáp án (Đề 2)

Câu 1:

Phần I: Trắc nghiệm

Đường tròn (C): $x^{2}$ + $y^{2}$ - 2x + 4y - 3 = 0 có tâm I, bán kính R là:

A. I(-1;2), R = $\sqrt{2}$

B. I(-1;2), R = 2 $\sqrt{2}$

C. I(1;-2), R = $\sqrt{2}$

D. I(1;-2), R = 2 $\sqrt{2}$

Xem đáp án

Đáp án: D

(C): $x^{2}$ + $y^{2}$ - 2x + 4y - 3 = 0 ⇔ (x - 1 $)^{2}$ + (y + 2 $)^{2}$ = 8

Suy ra, I(1;-2), R = $\sqrt{8}$ = 2 $\sqrt{2}$

Câu 2:

Tìm các giá trị của tham số m để x2 - 2x - m ≥ 0 ∀x

A. m ≤ 0

B. m < 0

C. m ≤ -1

D. m < -1

Xem đáp án

Đáp án: D

$x^{2}$ - 2x - m ≥ 0

Ta có: Δ' = (-1 $)^{2}$ -1.(-m) = m + 1

Để $x^{2}$ - 2x - m ≥ 0 ∀x thì Δ' < 0 ⇔ m + 1 < 0 ⇔ m < -1

Câu 3:

Hình vuông ABCD có A(2;1), C(4;3). Tọa độ của đỉnh B có thể là:

A. (-2;-3)

B. (1;4)

C. (-4;-1)

D. (-3;-2)

Xem đáp án

Đáp án: B

A(2;1), C(4;3) ⇒

Gọi I là trung điểm của của AC ⇒ I(3;2)

Đường chéo BD là đường thẳng đi qua I và có vecto pháp tuyến là

BD: 2(x - 3) + 2(y - 2) = 0 ⇔ x + y - 5 = 0

Thay tọa độ các điểm vào đường thẳng BD ta thấy tọa độ điểm ở đáp án B thỏa mãn phương trình đường thẳng BD.

Câu 4:

Cho đường thẳng Δ: x - 2y + 3 = 0. Vecto nào sau đây không là vecto chỉ phương của Δ?

A. (4;-2)

B. (-2;-1)

C. (2;1)

D. (4;2)

Xem đáp án

Đáp án: A

Δ: x - 2y + 3 = 0 có

Ta thấy: (4;-2).(1;-2) = 4.1 + (-2).(-2) = 4 + 4 = 8 ≠ 0

Nên (4;-2) không phải là vecto chỉ phương của Δ

Câu 5:

Tìm m để phương trình (m-1) $x^{2}$ - 2mx + 3m - 2 = 0 có hai nghiệm dương phân biệt?

A. m < 0,1 < m < 2

B. 1 < m < 2

C. m > 2

D. m < 1/2

Xem đáp án

Đáp án: B

(m - 1) $x^{2}$ - 2mx + 3m - 2 = 0 (*)

Để phương trình (*) có hai nghiệm dương phân biệt thì:

Câu 6:

Cho Elip (E): 4 $x^{2}$ + 5 $y^{2}$ = 20. Diện tích hình chữ nhật cơ sở của E là:

A. 2 $\sqrt{5}$

B. 80

C. 8 $\sqrt{5}$

D.40

Xem đáp án

Đáp án: C

(E): 4 $x^{2}$ + 5 $y^{2}$ = 20

Ta có: $a^{2}$ = 5 ⇒ a = $\sqrt{5}$ , $b^{2}$ = 4 ⇒ b = 2

Hình chữ nhật cơ sở có độ dài hai cạnh lần lượt là 2a = 2 $\sqrt{5}$ , 2b = 4

Suy ra, diện tích hình chữ nhật cơ sở là: 2 $\sqrt{5}$ .4 = 8 $\sqrt{5}$

Câu 7:

Cho $\tan x = 2 (π < x < \frac{3 π}{2})$ . Giá trị của $\sin (x + \frac{π}{3})$ là:

A. $\frac{2 - \sqrt{3}}{2 \sqrt{5}}$

B. $- \frac{2 + \sqrt{3}}{2 \sqrt{5}}$

C. $\frac{2 + \sqrt{3}}{2 \sqrt{5}}$

D. $\frac{- 2 + \sqrt{3}}{2 \sqrt{5}}$

Xem đáp án

Đáp án: B

Ta có:

Mặt khác,

Ta có:

Câu 8:

Tam giác ABC có A(1;2), B(0;4), C(3;1). Góc ∠BAC của tam giác ABC là:

A. 90 $°$

B. 36 $°$ 52'

C. 143 $°$ 7'

D. 53 $°$ 7'

Xem đáp án

Đáp án: C

Ta có: A(1;2), B(0;4), C(3;1)

Câu 9:

Tập nghiệm của hệ bất phương trình $\{\begin{cases} 3 - x \geq 0 \\ x + 1 \geq 0 \end{cases}$ là:

A. R

B. [-1;3]

C. ∅

D. (-1;3]

Xem đáp án

Đáp án: B

Ta có:

Vậy tập nghiệm của hệ bất phương trình là: [-1;3]

Câu 10:

Bất phương trình $\sqrt{x^{2} + 5 x + 3} < 2 x + 1$ có tập nghiệm là:

A. $(1; + \infty)$

B. $(- \frac{1}{2}; 1)$

C. $(- \frac{2}{3}; - \frac{1}{2}) \cup (1; + \infty)$

D. $(- 2; - 1)$

Xem đáp án

Đáp án: A

Ta có:

Câu 11:

Với giá trị nào của m thì hai đường thẳng d: 2x + ( $m^{2}$ +1)y - 3 = 0 và d': x + my - 10 = 0 song song?

A. m = 1 hoặc m = 2

B. m = 1 hoặc m = 0

C. m = 2

D. m = 1

Xem đáp án

Đáp án: D

Để hai đường thẳng d: 2x + ( $m^{2}$ + 1)y - 3 = 0 và d': x + my - 10 = 0 song song thì:

⇒ 2m = $m^{2}$ + 1 ⇔ $m^{2}$ - 2m + 1 = 0 ⇔ (m - 1 $)^{2}$ = 0 ⇔ m = 1

Vậy với m = 1 thì d và d’ song song với nhau.

Câu 12:

Cho elip (E) đi qua điểm A(-3;0) và có tâm sai e = 5/6. Tiêu cự của (E) là:

A. 10

B. 5/3

C. 5

D. 10/3

Xem đáp án

Đáp án: C

Cho elip (E) đi qua điểm A(-3;0) và có tâm sai

Giả sử elip có dạng:

Vì (E) đi qua điểm

Vậy elip (E) có tiêu cự là:

Câu 13:

Đẳng thức nào không đúng với mọi x?

A. $\cos^{2} 3 x = \frac{1 + \cos 6 x}{2}$

B. $\cos 2 x = 1 - 2 \sin^{2} x$

C. $\sin 2 x = 2 \sin x \cos x$

D. $\sin^{2} 2 x = \frac{1 + \cos 4 x}{2}$

Xem đáp án

Đáp án: D

Áp dụng công thức hạ bậc ta có:

Vậy đáp án D sai

Câu 14:

Cho đường tròn (C): $x^{2}$ + $y^{2}$ - 2x - 4y - 4 = 0. Phương trình tiếp tuyến của đường tròn tại điểm A(1;-1) là:

A. x + 1 = 0

B. y + 1 = 0

C. x + y + 1 = 0

D. x - y + 1 = 0

Xem đáp án

Đáp án: B

(C): $x^{2}$ + $y^{2}$ - 2x - 4y - 4 = 0 ⇔ (x - 1 $)^{2}$ + (y - 2 $)^{2}$ = 9

Đường tròn (C) có tâm I(1;2)

Tiếp tuyến của đường tròn tại A là đường thẳng đi qua A và nhận IA làm vecto pháp tuyến: -3(y + 1) = 0 ⇔ y + 1 = 0

Câu 15:

Cho $\cos x = \frac{1}{3} (- \frac{π}{3} < x < 0)$ . Giá trị của tan⁡2x là:

A. $\frac{\sqrt{5}}{2}$

B. $\frac{4 \sqrt{2}}{7}$

C. $- \frac{\sqrt{5}}{2}$

D. $- \frac{4 \sqrt{2}}{7}$

Xem đáp án

Đáp án: B

Ta có:

Câu 16:

Rút gọn biểu thức sau ta được biểu thức nào sau đây?

$A = \frac{c o s 2 x + \sin 2 x + \sin^{2} x}{2 \sin x + c o s x}$

A. cosx

B. s⁡inx

C. tanx

D. cotx

Xem đáp án

Đáp án: A

Ta có:

$A = \frac{c o s 2 x + \sin 2 x + \sin^{2} x}{2 \sin x + c o s x}$

Câu 17:

Tập nghiệm của bất phương trình | $x^{2}$ - 1| > 2x - 1 là:

A. (0;2)

B. (-1- $\sqrt{3}$ ;-1+√√)

C.(- $\infty$ ;-1+√√) ∪ (2;+ $\infty$ )

D. (- $\infty$ ;0) ∪ (2;+ $\infty$ )

Xem đáp án

Đáp án: C

Ta có:

Vậy tập nghiệm của bất phương trình là: (- $\infty$ ;-1+ $\sqrt{3}$ ) ∪ (2;+ $\infty$ )

Câu 18:

Trong mặt phẳng Oxy, khoảng cách từ điểm M(3;-4) đến đường thẳng d: 3x - 4y - 1 = 0 là:

A. $\frac{8}{5}$

B. $\frac{12}{5}$

C. $\frac{16}{5}$

D. $\frac{24}{5}$

Xem đáp án

Đáp án: D

Khoảng cách từ điểm M(3;-4) đến đường thẳng d: 3x - 4y - 1 = 0 là:

Câu 19:

Giá trị nhỏ nhất của $\sin^{6} x$ + $c o s^{6} x$ là:

A. 0

B. $\frac{1}{2}$

C. $\frac{1}{4}$

D. $\frac{1}{8}$

Xem đáp án

Đáp án: C

Ta có:

$\sin^{6} x$ + $c o s^{6} x$ = ( $\sin^{2} x)^{3}$ + ( $\cos^{2} x)^{3}$

= ( $\sin^{2} x$ + $c o s^{2} x$ )( $\sin^{4} x$ - $\sin^{2} x \cos^{2} x$ + $c o s^{4} x$ )

= $\sin^{4} x$ - $\sin^{2} x \cos^{2} x$ + $c o s^{4} x$

= ( $\sin^{2} x$ + $\cos^{2} x)^{2}$ - 3 $\sin^{2} x \cos^{2} x$

= 1 - 3 $\sin^{2} x \cos^{2} x$

= 1 - (3/4) $\sin^{2} 2 x$

Vì

Vậy giá trị nhỏ nhất của $\sin^{6} x$ + $c o s^{6} x$ là 1/4

Dấu “=” xảy ra ⇔ $\sin^{2} 2 x$ = 1 ⇔ sin⁡2x = 1 hoặc sin⁡2x = -1

Câu 20:

Phương trình tham số của đường thẳng đi qua A(2;7) có vecto chỉ phương $\vec{u} = (1; 6)$ là:

A. $\{\begin{cases} x = 1 + 2 t \\ y = 6 + 7 t \end{cases}$

B. $\{\begin{cases} x = 2 + t \\ y = 7 + 6 t \end{cases}$

C. $\{\begin{cases} x = 1 - 2 t \\ y = 6 - 7 t \end{cases}$

D. $\{\begin{cases} x = 2 - t \\ y = 7 - 6 t \end{cases}$

Xem đáp án

Đáp án: B

Phương trình tham số của đường thẳng đi qua A(2;7) có vecto chỉ phương

Câu 21:

Phần II: Tự luận

a) Giải bất phương trình và hệ bất phương trình sau:

b) Tìm các giá trị của m để hàm số $y = \sqrt{(m + 10) x^{2} - 2 (m - 2) x + 1}$ có tập xác định D = R

Xem đáp án

a) Ta có:

Vậy tập nghiệm của bất phương trình là: [4;13]

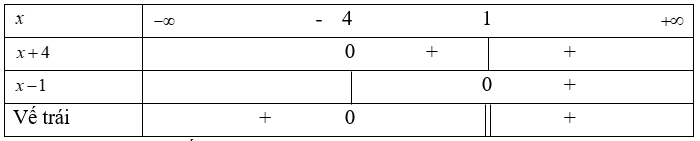
Ta có bảng xét dấu vế trái của bất phương trình (1):

Vậy tập nghiệm của bất phương trình (1) là: (- $\infty$ ;-4) ∪ (1;+ $\infty$ )

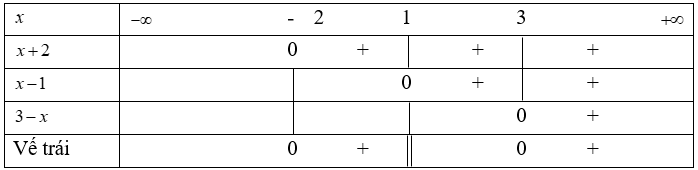
Ta có bảng xét dấu vế trái của bất phương trình (2) là:

Vậy tập nghiệm của bất phương trình (2) là: ( $- \infty$ ;-2) ∪ (1;3)

Vậy tập nghiệm của hệ bất phương trình là: ( $- \infty$ ;-4) ∪ (1;3)

b) Để hàm số $y = \sqrt{(m + 10) x^{2} - 2 (m - 2) x + 1}$ có tập xác định D = R thì (m + 10) $x^{2}$ - 2(m - 2)x + 1 ≥ 0, ∀x

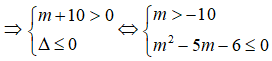
Vậy với -1 ≤ m ≤ 6 thì hàm số $y = \sqrt{(m + 10) x^{2} - 2 (m - 2) x + 1}$ có tập xác định D = R

Câu 22:

Tam giác ABC có $\sin A = \frac{\sin B + \sin C}{c o s B + \cos C}$ . Chứng minh tam giác ABC vuông.

Xem đáp án

Ta có:

Vì:

Suy ra, tam giác ABC vuông tại A

Câu 23:

Trong mặt phẳng tọa độ cho hai điểm A(3;0), B(0;2) và đường thẳng d: x + y = 0.

a) Lập phương trình tham số của đường thẳng Δ đi qua A và song song với d

b) Lập phương trình đường tròn đi qua A,B và có tâm thuộc đường thẳng d

c) Lập phương trình chính tắc của elip đi qua điểm B và có tâm sai $e = \frac{\sqrt{5}}{3}$

Xem đáp án

Đường thẳng Δ song song với d ⇒ Δ: x + y + c = 0, (c ≠ 0)

Vì Δ đi qua A ⇒ 3 + 0 + c = 0 ⇒ c = -3(tm)

Vậy đường thẳng Δ có dạng: x+y-3=0

Vì đường tròn có tâm I thuộc d nên I(a;-a)

Vì đường tròn đi qua A, B nên I $A^{2}$ = I $B^{2}$ ⇒ (3 - a $)^{2}$ + $a^{2}$ = $a^{2}$ + (2 + a $)^{2}$ ⇔ (3 - a $)^{2}$ = (2 + a $)^{2}$

Vậy phương trình đường tròn có dạng:

Ta có:

Giả sử elip (E) có dạng:

Vì (E) đi qua B nên:

Mà

Vậy phương trình chính tắc của elip (E) là:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Top 4 Đề thi Toán 10 Học kì 2 có đáp án

Đề thi Học kì 2 Toán 10 có đáp án (Đề 2)

Danh sách câu hỏi

Phần I: Trắc nghiệm

Phần II: Tự luận

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương