Trắc nghiệm Toán 10 Bài 3. Đường tròn trong mặt phẳng tọa độ có đáp án
-
313 lượt thi
-
15 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Tọa độ tâm I và bán kính R của đường tròn (C): (x – 1)2 + (y + 3)2 = 16 là:
Đáp án đúng là: B
Đường tròn (C) có tâm I(1; –3), bán kính R = √16 = 4.
Vậy ta chọn phương án B.
Câu 2:
Đường tròn (C) có tâm I(1; –5) và đi qua O(0; 0) có phương trình là:
Đáp án đúng là: C
Với I(1; –5) ta có: →OI=(1;−5)
Đường tròn (C) có tâm I(1; –5) và đi qua O(0; 0) nên có bán kính là:
R = OI = √12+(−5)2=√26
Suy ra R2 = 26.
Vậy phương trình đường tròn (C) là:
(x – 1)2 + (y + 5)2 = 26.
Do đó ta chọn phương án C.
Câu 3:
Đường tròn (C): x2 + y2 + 12x – 14y + 4 = 0 viết được dưới dạng:
Đáp án đúng là: B
Phương trình (C) có dạng: x2 + y2 – 2ax – 2by + c = 0, với a = –6, b = 7, c = 4.
Suy ra tâm I(–6; 7).
Ta có R2 = a2 + b2 – c = 36 + 49 – 4 = 81.
Vậy phương trình của đường tròn (C) là: (x + 6)2 + (y – 7)2 = 81.
Do đó ta chọn phương án B.
Câu 4:
Đường tròn (C) có tâm I(2; –3) và tiếp xúc với trục Oy có phương trình là:
Đáp án đúng là: C
Phương trình trục Oy: x = 0.
Đường tròn (C) có tâm I(2; –3) và tiếp xúc với trục Oy nên có bán kính là:
R = d(I, Oy) = |2|√12+02=2
Vậy phương trình đường tròn (C): (x – 2)2 + (y + 3)2 = 4.
Do đó ta chọn phương án C.
Câu 5:
Đường tròn (C): x2 + y2 – 6x + 2y + 6 = 0 có tâm I và bán kính R là:
Đáp án đúng là: C
Phương trình đã cho có dạng: x2 + y2 – 2ax – 2by + c = 0, với a = 3, b = –1, c = 6.
Suy ra tâm I(3; –1).
Ta có R2 = a2 + b2 – c = 9 + 1 – 6 = 4.
Suy ra R = 2.
Vậy đường tròn (C) có tâm I(3; –1), bán kính R = 2.
Do đó ta chọn phương án C.
Câu 6:
Tọa độ tâm I của đường tròn đi qua ba điểm A(0; 4), B(2; 4), C(4; 0) là:
Đáp án đúng là: D
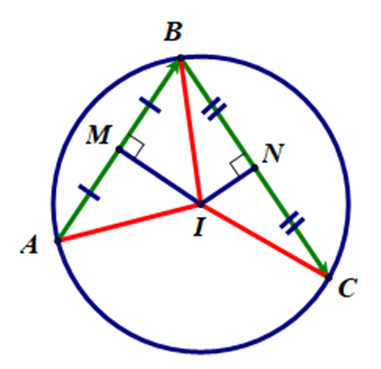
Gọi M, N lần lượt là trung điểm của AB, BC.
Vì M là trung điểm AB nên ta có {xM=xA+xB2=0+22=1yM=yA+yB2=4+42=4
Suy ra M(1; 4).
Tương tự, ta có N(3; 2).
Đường trung trực ∆1 của đoạn thẳng AB đi qua điểm M(1; 4) và có vectơ pháp tuyến →AB=(2;0)
Suy ra phương trình ∆1 là: 2(x – 1) + 0(y – 4) = 0 ⇔ x – 1 = 0.
Tương tự, ta có phương trình đường trung trực ∆2 của đoạn thẳng BC đi qua điểm N(3; 2) và có vectơ pháp tuyến →BC=(2;−4) là:
2(x – 3) – 4(y – 2) = 0 Û x – 2y + 1 = 0.
Vì IA = IB = IC = R nên I cách đều ba điểm A, B, C.
Do đó I nằm trên đường trung trực ∆1 và I cũng nằm trên đường trung trực ∆2.
Hay I là giao điểm của ∆1 và ∆2.
Khi đó tọa độ I là nghiệm của hệ phương trình: {x−1=0x−2y+1=0⇔{x=1y=1
Suy ra tọa độ tâm I(1; 1).
Vậy ta chọn phương án D.
Câu 7:
Trong các phương trình sau, phương trình nào là phương trình của một đường tròn?
Đáp án đúng là: D
Phương trình đường tròn có dạng: x2 + y2 – 2ax – 2by + c = 0 (điều kiện: a2 + b2 – c > 0).
• Ta thấy phương trình ở phương án A và C không có dạng như trên.
Nên ta loại phương án A, C.
• Ta xét phương án B:
Ta có a = 1, b = 4, c = 20.
Suy ra a2 + b2 – c = 1 + 16 – 20 = –3 < 0.
Do đó phương trình ở phương án B không phải là một phương trình đường tròn.
Vì vậy ta loại phương án B.
Đến đây ta có thể chọn phương án D.
• Ta xét phương án D:
Ta có a = 2, b = –3, c = –12.
Suy ra a2 + b2 – c = 4 + 9 + 12 = 25 > 0.
Do đó phương trình ở phương án D là một phương trình đường tròn.
Vậy ta chọn phương án D.
Câu 8:
Tọa độ tâm I và bán kính R của đường tròn (C): 16x2 + 16y2 + 16x – 8y – 11 = 0 là:
Đáp án đúng là: D
Ta có 16x2 + 16y2 + 16x – 8y – 11 = 0.
Suy ra x2+y2+x−12y−1116=0
Phương trình (C) có dạng: x2 + y2 – 2ax – 2by + c = 0, với a=−12,
Suy ra tâm
Ta có R2 = a2 + b2 – c =
Suy ra R = 1.
Vậy đường tròn (C) có tâm , bán kính R = 1.
Do đó ta chọn phương án D.
Câu 9:
Đường tròn (C) đi qua hai điểm A(–1; 2), B(–2; 3) và có tâm I thuộc đường thẳng ∆: 3x – y + 10 = 0. Phương trình đường tròn (C) là:
Đáp án đúng là: D
Giả sử I(a; b) ∈ ∆: 3x – y + 10 = 0.
Suy ra 3a – b + 10 = 0
⇔ b = 3a + 10.
Khi đó ta có I(a; 3a + 10)
Suy ra
Và
Ta có IA = IB (= R).
⇔ IA2 = IB2
⇔ (–1 – a)2 + (–3a – 8)2 = (–2 – a)2 + (–3a – 7)2
⇔ 1 + 2a + a2 + 9a2 + 48a + 64 = 4 + 4a + a2 + 9a2 + 42a + 49
⇔ 4a = –12
⇔ a = –3.
Với a = –3, ta có b = 3a + 10 = 3.(–3) + 10 = 1.
Suy ra I(–3; 1).
Ta có R2 = IA2 = (–1 – a)2 + (–3a – 8)2 = [–1 – (–3)]2 + [–3.(–3) – 8]2 = 5.
Vậy phương trình đường tròn (C): (x + 3)2 + (y – 1)2 = 5.
Do đó ta chọn phương án D.
Câu 10:
Cho phương trình x2 + y2 – 2mx – 4(m – 2)y + 6 – m = 0. Điều kiện của m để phương trình đã cho là một phương trình đường tròn là:
Đáp án đúng là: B
Phương trình đã cho có dạng x2 + y2 – 2ax – 2by + c = 0, với a = m, b = 2(m – 2), c = 6 – m.
Ta có a2 + b2 – c = m2 + 4(m2 – 4m + 4) – 6 + m = 5m2 – 15m + 10.
Để phương trình đã cho là phương trình đường tròn thì a2 + b2 – c > 0.
Nghĩa là 5m2 – 15m + 10 > 0
⇔ m < 1 hoặc m > 2.
Vậy m ∈ (–∞; 1) ∪ (2; +∞) thỏa mãn yêu cầu bài toán.
Do đó ta chọn phương án B.
Câu 11:
Cho đường tròn (C): x2 + y2 + 5x + 7y – 3 = 0. Khoảng cách từ tâm của (C) đến trục hoành bằng:
Đáp án đúng là: C
Phương trình đã cho có dạng: x2 + y2 – 2ax – 2by + c = 0, với , , c = –3.
Suy ra tâm
Trục Ox có phương trình là y = 0.
Ta có
Vậy ta chọn phương án C.
Câu 12:
Đường tròn (C) có tâm I thuộc đường thẳng d: x + 3y + 8 = 0, đi qua điểm A(–2; 1) và tiếp xúc với đường thẳng ∆: 3x – 4y + 10 = 0. Phương trình đường tròn (C) là:
Đáp án đúng là: D
Gọi I(a; b) là tâm của đường tròn (C).
Ta có I ∈ d.
Suy ra a + 3b + 8 = 0 ⇔ a = –3b – 8.
Ta có đường tròn (C) đi qua điểm A(–2; 1) nên AI = R (1).
Lại có đường tròn (C) tiếp xúc với đường thẳng ∆ nên d(I, ∆) = R (2).
Từ (1), (2), ta suy ra IA = d(I, ∆).
⇔ 25(9b2 + 36b + 36 + b2 – 2b + 1) = 169b2 + 364b + 196
⇔ 81b2 + 486b + 729 = 0
⇔ b = –3.
Với b = –3, ta có a = –3b – 8 = –3.(–3) – 8 = 1.
Khi đó ta có I(1; –3).
R = AI =
Vậy phương trình đường tròn (C) là: (x – 1)2 + (y + 3)2 = 25.
Vậy ta chọn phương án D.
Câu 13:
Cho đường tròn (C): (x – 2)2 + (y + 4)2 = 25, biết tiếp tuyến vuông góc với đường thẳng d: 3x – 4y + 5 = 0. Phương trình tiếp tuyến của (C) là:
Đáp án đúng là: D
Gọi ∆ là tiếp tuyến cần tìm.
Đường tròn (C) có tâm I(2; –4), bán kính R = 5.
Đường thẳng d có vectơ pháp tuyến
Theo đề, ta có ∆ ⊥ d nên ∆ nhận vectơ pháp tuyến của d làm vectơ chỉ phương.
Do đó ∆ có vectơ chỉ phương
Khi đó ∆ có vectơ pháp tuyến
Vì vậy phương trình tiếp tuyến cần tìm có dạng ∆: 4x + 3y + c = 0.
Vì ∆ là tiếp tuyến của đường tròn (C) nên d(I, ∆) = R.
⇔ |c – 4| = 25
⇔ c – 4 = 25 hoặc c – 4 = –25
⇔ c = 29 hoặc c = –21.
Vậy ∆: 4x + 3y + 29 = 0 hoặc ∆: 4x + 3y – 21 = 0.
Do đó ta chọn phương án D.
Câu 14:
Cho phương trình (C): x2 + y2 – 2(m + 1)x + 4y – 1 = 0. Với giá trị nào của m thì đường tròn (C) có bán kính nhỏ nhất?
Đáp án đúng là: B
Phương trình đường tròn (C) có dạng: x2 + y2 – 2ax – 2by + c = 0, với a = m + 1, b = –2, c = –1.
Ta có R2 = a2 + b2 – c = (m + 1)2 + 4 + 1 = (m + 1)2 + 5.
Đường tròn (C) có bán kính nhỏ nhất khi và chỉ khi biểu thức (m + 1)2 + 5 đạt giá trị nhỏ nhất.
Ta có: (m + 1)2 ≥ 0, ∀m ∈ ℝ.
⇔ (m + 1)2 + 5 ≥ 5, ∀m ∈ ℝ.
Vậy giá trị nhỏ nhất của biểu thức (m + 1)2 + 5 là 5.
Dấu “=” xảy ra ⇔ m = –1.
Vậy m = –1 thỏa mãn yêu cầu bài toán.
Do đó ta chọn phương án B.
Câu 15:
Cho đường tròn (C): x2 + y2 – 2x – 4y + 1 = 0. Gọi d1, d2 lần lượt là tiếp tuyến của đường tròn (C) tại điểm M(3; 2), N(1; 0). Tọa độ giao điểm của d1 và d2 là:
Đáp án đúng là: A
Ta viết phương trình d1:
Ta có 32 + 22 – 2.3 – 4.2 + 1 = 0 (đúng).
Do đó điểm M ∈ (C).
Phương trình đường tròn (C) có dạng: x2 + y2 – 2ax – 2by + c = 0, với a = 1, b = 2, c = 1.
Suy ra tâm I(1; 2), bán kính R =
Phương trình d1 là: (1 – 3)(x – 3) + (2 – 2)(y – 2) = 0
⇔ –2(x – 3) = 0 ⇔ x – 3 = 0.
Tương tự, ta viết phương trình d2:
Ta có 12 + 02 – 2.1 – 4.0 + 1 = 0 (đúng).
Do đó N ∈ (C).
Phương trình d2 là: (1 – 1)(x – 1) + (2 – 0)(y – 0) = 0
⇔ y = 0.
Gọi A là giao điểm của d1 và d2.
Suy ra tọa độ A là nghiệm của hệ phương trình:
Khi đó ta có tọa độ A(3; 0).
Vậy ta chọn phương án A.
