10 câu hỏi trắc nghiệm thuộc Dạng 5: Chứng minh hai vectơ cùng phương có đáp án

Câu 1:

Cho $\vec{a}$ và $\vec{b}$ không cùng phương và hai vectơ $\vec{x} = 2 \vec{a} + \vec{b}$ và $\vec{y} = - 4 \vec{a} - 2 \vec{b}$ . Khẳng định nào sau đây là đúng ?

A.

\vec{x}

và

\vec{y}

cùng phương, cùng hướng;

B.

\vec{x}

và

\vec{y}

không cùng phương;

C.

\vec{x}

và

\vec{y}

bằng nhau;

D.

\vec{x}

và

\vec{y}

cùng phương, ngược hướng.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: D.

Ta có:

$\vec{x} = 2 \vec{a} + \vec{b}$

$\vec{y} = - 4 \vec{a} - 2 \vec{b} = - 2 (2 \vec{a} + \vec{b}) = - 2 \vec{x}$

Vì – 2 < 0

Do đó, $\vec{x}$ và $\vec{y}$ cùng phương, ngược hướng.

Câu 2:

Cho hình bình hành ABCD. Khẳng định nào sau đây là đúng ?

A.

\vec{A B}

và

\vec{C D}

cùng phương, cùng hướng;

B.

\vec{A B}

và

\vec{C D}

cùng phương, ngược hướng;

C.

\vec{A D}

và

\vec{C D}

cùng phương, cùng hướng;

D.

\vec{A D}

và

\vec{C B}

cùng phương, cùng hướng.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B.

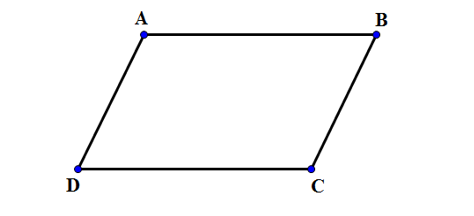
Xét hình bình hành ABCD có:

AB // CD

Do đó, $\vec{A B}$ và $\vec{C D}$ cùng phương, ngược hướng.

Câu 3:

Cho hình vuông ABCD tâm O. Khẳng định nào sau đây là sai ?

A.

\vec{A B}

và

\vec{C D}

cùng phương, ngược hướng;

B.

\vec{A D}

và

\vec{C B}

cùng phương, ngược hướng;

C.

\vec{A O}

và

\vec{C O}

không cùng phương;

D.

\vec{A O}

và

\vec{O D}

không cùng phương.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C.

Cho hình vuông ABCD tâm O. Khẳng định nào sau đây là sai ? (ảnh 1)

Vì ABCD là hình vuông nên $\vec{A B}$ và $\vec{C D}$ cùng phương, ngược hướng; $\vec{A D}$ và $\vec{C B}$ cùng phương, ngược hướng.

Lại có $\vec{A O}$ và $\vec{C O}$ có cùng giá là đường thẳng AC.

Do đó, $\vec{A O}$ và $\vec{C O}$ cùng phương.

Vậy đáp án C sai.

Câu 4:

Cho các vectơ $\vec{a}$ và $\vec{b}$ không cùng phương và $\vec{x} = \vec{a} - 3 \vec{b}$ , $\vec{y} = 2 \vec{a} + 6 \vec{b}$ và $\vec{z} = - 3 \vec{a} + \vec{b}$ . Khẳng định nào sau đây là đúng ?

A.

\vec{y}

,

\vec{z}

cùng phương, ngược hướng;

B.

\vec{y}

,

\vec{z}

cùng phương, cùng hướng;

C.

\vec{y}

,

\vec{x}

cùng phương, ngược hướng;

D.

\vec{y}

,

\vec{x}

cùng phương, cùng hướng.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C.

Ta có:

$\vec{x} = \vec{a} - 3 \vec{b}$

$\vec{y} = 2 \vec{a} + 6 \vec{b} = - 2 (\vec{a} - 3 \vec{b}) = - 2 \vec{x}$

Vì – 2 < 0

Vậy $\vec{y}$ , $\vec{x}$ cùng phương, ngược hướng.

Câu 5:

Cho các vectơ $\vec{a}$ và $\vec{b}$ không cùng phương và $\vec{u} = 2 \vec{a} - 3 \vec{b}$ và $\vec{v} = 3 \vec{a} - 9 \vec{b}$ . Khẳng định nào sau đây là đúng ?

A.

\vec{u}

và

\vec{v}

cùng phương, ngược hướng;

B.

\vec{u}

và

\vec{v}

cùng phương, cùng hướng;

C.

\vec{u}

và

\vec{v}

bằng nhau;

D.

\vec{u}

và

\vec{v}

không cùng phương.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: D.

Ta có:

Giả sử tồn tại số thực k sao cho $\vec{u} = k \vec{v}$ .

$\Leftrightarrow 2 \vec{a} - 3 \vec{b} = k (3 \vec{a} - 9 \vec{b})$

$\Leftrightarrow (3 k - 2) \vec{a} - (9 k - 3) \vec{b} = \vec{0}$

Mà $\vec{a}$ và $\vec{b}$ không cùng phương nên ta có:

$\{\begin{cases} 3 k - 2 = 0 \\ 9 k - 3 = 0 \end{cases} \Leftrightarrow \{\begin{cases} k = \frac{2}{3} \\ k = \frac{1}{3} \end{cases}$

Vậy không tồn tại k thỏa mãn.

Do đó, $\vec{u}$ và $\vec{v}$ không cùng phương.

Câu 6:

Cho các vectơ $\vec{a}$ và $\vec{b}$ không cùng phương và: $\vec{x} = 5 \vec{a} - 2 \vec{b}$ , $\vec{y} = 2 \vec{a} - 5 \vec{b}$ và $\vec{z} = 10 \vec{a} - 4 \vec{b}$ . Khẳng định nào sau đây là đúng ?

A.

\vec{y}

,

\vec{z}

cùng phương, ngược hướng;

B.

\vec{y}

,

\vec{z}

cùng phương, cùng hướng;

C.

\vec{z}

,

\vec{x}

cùng phương, ngược hướng;

D.

\vec{z}

,

\vec{x}

cùng phương, cùng hướng.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: D.

Ta có:

$\vec{x} = 5 \vec{a} - 2 \vec{b}$

$\vec{z} = 10 \vec{a} - 4 \vec{b} = 2 (5 \vec{a} - 2 \vec{b}) = 2 \vec{x}$

Có: 2 > 0

Do đó, $\vec{z}$ , $\vec{x}$ cùng phương, cùng hướng.

Câu 7:

Cho các vectơ $\vec{a}$ , $\vec{b}$ , $\vec{c}$ không cùng phương và: $\vec{u} = \vec{a} - 2 \vec{b} + \vec{c}$ , $\vec{v} = 2 \vec{a} - 4 \vec{b} + 2 \vec{c}$ và $\vec{w} = 2 \vec{a} - 4 \vec{b} - 2 \vec{c}$ . Khẳng định nào sau đây là đúng ?

A.

\vec{u}

,

\vec{v}

cùng phương, ngược hướng;

B.

\vec{u}

,

\vec{w}

cùng phương, cùng hướng;

C.

\vec{v}

,

\vec{w}

cùng phương, ngược hướng;

D.

\vec{u}

,

\vec{v}

cùng phương, cùng hướng.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: D.

$\vec{u} = \vec{a} - 2 \vec{b} + \vec{c}$

$\vec{v} = 2 \vec{a} - 4 \vec{b} + 2 \vec{c} = 2 (\vec{a} - 2 \vec{b} + \vec{c}) = 2 \vec{u}$

Có: 2 > 0

Do đó, $\vec{u}$ , $\vec{v}$ cùng phương, cùng hướng.

Câu 8:

Cho các vectơ $\vec{a}$ , $\vec{b}$ không cùng phương và: $\vec{u} = \vec{a} - \vec{b}$ , $\vec{v} = 2 \vec{a} - 4 \vec{b}$ và $\vec{w} = 2 \vec{a} - 2 \vec{b}$ . Khẳng định nào sau đây là đúng ?

A.

\vec{u}

,

\vec{v}

cùng phương, ngược hướng;

B.

\vec{u}

,

\vec{v}

không cùng phương;

C.

\vec{v}

,

\vec{w}

cùng phương, ngược hướng;

D.

\vec{u}

,

\vec{v}

cùng phương, cùng hướng.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B.

Giả sử tồn tại số thực k sao cho:

$\vec{u} = k \vec{v}$

$\Leftrightarrow \vec{a} - \vec{b} = k (2 \vec{a} - 4 \vec{b})$

$\Leftrightarrow \vec{a} (2 k - 1) + \vec{b} (- 4 k + 1) = \vec{0}$

Mà $\vec{a}$ , $\vec{b}$ không cùng phương nên điều này tương đương với:

$\{\begin{cases} 2 k - 1 = 0 \\ - 4 k + 1 = 0 \end{cases} \Leftrightarrow \{\begin{cases} k = \frac{1}{2} \\ k = \frac{1}{4} \end{cases}$

Vậy không tồn tại số thực k thỏa mãn

Do đó, $\vec{u}$ , $\vec{v}$ không cùng phương.

Câu 9:

Cho hình chữ nhật ABCD, M là trung điểm của CD, N là trung điểm của AB. Số vectơ khác vectơ – không, có điểm đầu và điểm cuối là đỉnh của hình chữ nhật ABCD và cùng phương với $\vec{M N}$ là:

A. 2

B. 4

C. 3

D. 5

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B.

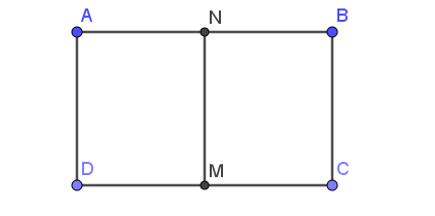
Cho hình chữ nhật ABCD, M là trung điểm của CD, N là trung điểm của AB. (ảnh 1)

Xét hình chữ nhật ABCD có:

M là trung điểm của CD, N là trung điểm của AB nên MN // AD // BC.

Do đó, các vectơ cùng phương với $\vec{M N}$ và có điểm đầu và điểm cuối là đỉnh của hình chữ nhật ABCD cần có giá là đường thẳng AD hoặc BC.

Các vectơ thỏa mãn yêu cầu đề bài là: $\vec{A D}, \vec{D A}, \vec{B C}, \vec{C B}$ .

Vậy có 4 vectơ.

Câu 10:

Cho lục giác đều ABCDEF tâm O. Số các vectơ khác vectơ – không, có điểm đầu và điểm cuối là đỉnh của hình lục giác đều ABCDEF và cùng phương với vectơ $\vec{O B}$ là:

A. 4

B. 6

C. 8

D. 10

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B.

Do ABCDEF là lục giác đều tâm O nên ta có: BE // CD // AF.

Hơn nữa đường thẳng OB trùng với đường thẳng BE.

Suy ra OB // CD // AF.

Do đó các vectơ khác vectơ – không, có điểm đầu và điểm cuối là đỉnh của hình lục giác đều ABCDEF và cùng phương với vectơ $\vec{O B}$ là: $\vec{B E}, \vec{E B}, \vec{C D}, \vec{D C}, \vec{A F}, \vec{F A}$ .

Vậy có 6 vectơ thỏa mãn.

CHỌN BỘ SÁCH BẠN MUỐN XEM

Trắc nghiệm Toán 10 CTST Bài 3. Tích của một số với một vectơ có đáp án

Dạng 5: Chứng minh hai vectơ cùng phương có đáp án

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương