Dạng 2: Tìm một điểm thỏa mãn một đẳng thức vectơ cho trước có đáp án
-
994 lượt thi
-
10 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Điểm I thỏa mãn là:
Hướng dẫn giải:
Đáp án đúng là: A.
Theo quy tắc ba điểm, ta có: .
Mà
Do đó:
Vậy I nằm trên nửa đường thẳng AB theo hướng từ B về A với .
Câu 2:
Điểm K thỏa mãn: là:
Hướng dẫn giải:
Đáp án đúng là: B.
Ta có:
Vậy K là trọng tâm của tam giác ABC.
Câu 3:
Cho tam giác ABC. Điểm P thỏa mãn với K tùy ý là điểm thỏa mãn:
Hướng dẫn giải:
Đáp án đúng là: A.
Ta có:
(quy tắc ba điểm)
Vậy tập hợp điểm P thỏa mãn .
Câu 4:
Cho tứ giác ABCD, I là trung điểm BD. Tìm điểm O thỏa mãn
Hướng dẫn giải:
Đáp án đúng là: B.
Ta có:
(quy tắc ba điểm)
(quy tắc trừ hai vectơ)
(quy tắc ba điểm)
(do I là trung điểm của BD nên )
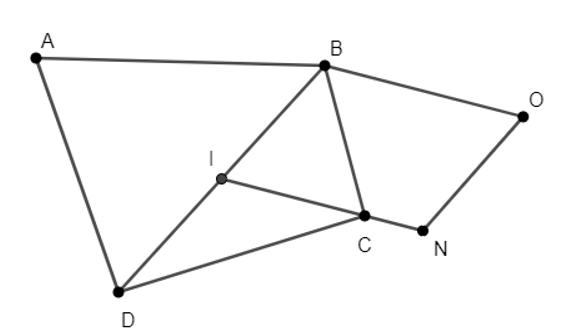
Vậy O là đỉnh của hình bình hành IBON với .
Câu 5:
Cho tứ giác ABCD và điểm O bất kì sao cho . Tìm điểm M thỏa mãn hệ thức .
Hướng dẫn giải:
Đáp án đúng là: A.
Ta có:
(quy tắc ba điểm)
(do )
⇔ MO = MA.
Vậy M thuộc đường trung trực của đoạn thẳng OA.
Câu 6:
Cho hai điểm A, B phân biệt. Xác định điểm M biết .
Hướng dẫn giải:
Đáp án đúng là: C.
Ta có:
(quy tắc ba điểm)
Vậy M nằm trên tia AB và AM = 3AB.
Câu 7:
Cho tứ giác ABCD. Gọi I là trung điểm của BC. Xác định điểm M sao cho: .
Đáp án đúng là: B.
Vì I là trung điểm của BC nên .
Ta có:
.
Vậy M là trung điểm của AI.
Câu 8:
Cho tứ giác ABCD. Gọi G là trọng tâm của tam giác BCD. Xác định điểm P sao cho: .
Hướng dẫn giải:
Đáp án đúng là: A.
Vì G là trọng tâm của tam giác BCD nên với điểm P thì .
Ta có:
.
Vậy P là trung điểm của AG.
Câu 9:
Cho tứ giác ABCD. Gọi K, H lần lượt là trung điểm của AB, CD. Xác định điểm N sao cho: .
Hướng dẫn giải:
Đáp án đúng là: D.
Vì K, H lần lượt là trung điểm của AB, CD nên .
Do đó ta có:
Vậy N là trung điểm của KH.
Câu 10:
Cho tam giác ABC vuông tại A. Điểm M bất kì nằm trong tam giác có hình chiếu xuống BC, CA, AB theo thứ tự là D, E, F. Tìm tập hợp điểm M biết cùng phương với .
Hướng dẫn giải:
Đáp án đúng là: A.
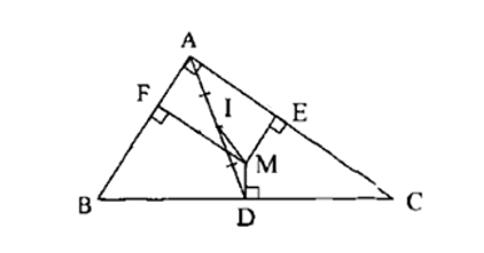
Xét tứ giác AEMF có: .
Do đó, AEMF là hình chữ nhật.
Áp dụng quy tắc hình bình hành ta có: .
Do đó ta có: .
Gọi I là trung điểm của AD.
Khi đó, .
Để cùng phương với thì cùng phương với
Do đó, cùng phương với (do PQ là đường trung bình của tam giác ABC song song với cạnh BC).
Vì M nằm trong tam giác ABC.
Do đó M thuộc đoạn PQ.
