100 câu trắc nghiệm Cung và góc lượng giác nâng cao (P4)
-
8835 lượt thi
-
25 câu hỏi
-
25 phút
Danh sách câu hỏi
Câu 4:
Nếu 5sin α = 3sin(α + 2β) thì :
Chọn C.
Áp dụng công thức cộng ; ta có :
5sin α = 3sin(α + 2β) ⇔ 5sin[(α + β) – β] = 3sin(α + β) + β]
⇔ 5sin(α + β)cos β – 5cos(α + β)sin β = 3sin(α + β)cos β + 3cos(α + β)sin β
⇔ 2sin(α + β)cos β = 8cos(α + β)sin β
Câu 5:
Biết và cot α, cot β, cot γ theo thứ tự lập thành một cấp số cộng. Tích số cot α.cot γ bằng :
Chọn C.
Ta có : , suy ra
Suy ra :
( rút gọn cả 2 vế cho cotβ)
⇒ cot α.cot γ =3.
Câu 6:
Cho tam giác ABC. Hãy chọn hệ thức đúng trong các hệ thức sau.
Chọn C.
Sử dụng công thức hạ bậc và biến đổi tổng thành tích ta có :
cos2A + cos2B + cos2C
= 1 + cos( A + B) .cos( A – B) + cos2C = 1 – cos C. cos( A – B) – cos C.cos( A + B)
= 1 – cosC[cos (A - B) + cos(A + B) ] = 1 + 2cosA. cosB.cosC
Câu 8:
Biểu thức
có kết quả rút gọn bằng
Chọn B.
Ta có tan 460 = cot 440 và cot180 = tan 720 nên
Suy ra: B = 2 – 1 = 1.
Câu 9:
Biểu thức 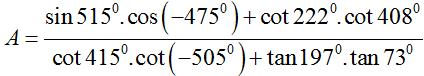 có kết quả rút gọn bằng
có kết quả rút gọn bằng
Chọn C.
Ta có: tan 1970 = tan170; tan 730 = cot 170; sin5150 = sin 1550; cos( -4750) = cos1150; cot2220 = cot420. Nên suy ra
Lại có; sin1550 = sin250; cos 1150 = -sin250; cot 480 = tan 420; cot ( -1450) = tan550
Câu 12:
Tính giá trị của biểu thức A = sin6x + cos6x + 3sin2x.cos2x.
Chọn B.
Ta có A = sin6x + cos6x + 3sin2x.cos2x.
= ( sin2x)3 + (cos2x)3 + 3sin2x.cos2x.
= (sin2x + cos2x)3 - 3sin2x.cos2x(sin2x + cos2x) + 3.sin2x.cos2x
= 1 - 3.sin2x.cos2x + 3.sin2x.cos2x = 1
Câu 15:
Rút gọn biểu thức C = 2( sin4x + cos4x + sin2x.cos2x) 2 - ( sin8x + cos8x)
Chọn C.
Ta có
C = [ ( sin2x + cos2x) – sin2cos2x]2 - [ ( sin4x + cos4x) 2 - 2sin4x.cos4x]
= 2[ 1-sin2x.cos2x]2 - [ ( sin2x + cos2x) 2 - 2sin2x.cos2x]2 + 2sin4x.cos4x
= 2[ 1-sin2x.cos2x]2 - [1-sin2x.cos2x]2 + 2sin4x.cos4x
= 2( 1 - 2sin2x.cos2x + sin4x.cos4x)- ( 1 - 4sin2xcos2x + 4sin4x.cos4x) + 2sin4x.cos4x
= 1.
Câu 16:
Hệ thức nào sai trong bốn hệ thức sau:
Chọn D.
Ta xét các đáp án.
+ A đúng vì
+ B đúng vì
+ C đúng vì
Câu 17:
Nếu biết 3.sin4x + 2cos4x = 98/81 thì giá trị biểu thức A = 2sin4x + 3cos4x bằng
Chọn D.
Ta có
Đặt
Câu 18:
Nếu sinx + cosx = 1/2 thì 3sinx + 2cosx bằng
Chọn A.
Ta có:
sinx + cosx = ½ nên ( sinx + cosx)2 = ¼
Do đó sinx. cosx = -3/8
Khi đó sinx; cosx là nghiệm của phương trình
Ta có sinx + cos x = ½ nên 2( sinx + cosx) = 13sinx+2cosx = sinx+2(sinx+cosx)=sinx+1
+) Với
+) Với
Câu 19:
Biết . Giá trị của biểu thức A = a.cos2x + 2b.sinx.cosx + c.sin2x bằng
Chọn B.
Ta có: A = a.cos2x + 2b.sinx.cosx + c.sin2x
Hay A( 1 + tan2x) = a + 2btanx + c.tan2x
Do đó: A = a.
Câu 20:
Nếu biết thì biểu thức
bằng
Chọn C.
Đặt
Hay
Suy ra:
Quy đồng khử mẫu ta được:
(a + b) 2t2 - 2b( a + b)t + b2 = 0
Suy ra
Vậy:
Câu 24:
Cho tam giác ABC và các mệnh đề :
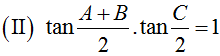
(III): cos(A + B - C) – cos 2C=0
Mệnh đề đúng là :
Chọn C.
+) Ta có:
nên (I) đúng
+) Tương tự ta có:
nên (II) đúng.
+) Ta có
A + B – C = π – 2C → cos(A + B + C) = cos(π – 2C) = -cos2C
⇔ cos(A + B – C) - cos(2C) = -2cos2C
nên (III) sai.

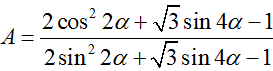
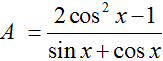
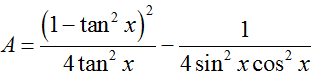
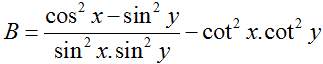
 bằng
bằng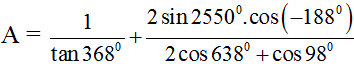 bằng :
bằng :