100 câu trắc nghiệm Cung và góc lượng giác nâng cao (P3)
-
8833 lượt thi
-
25 câu hỏi
-
25 phút
Danh sách câu hỏi
Câu 1:
Cho hai góc nhọn a và b với tan a = 1/7 và tan b = 3/4. Tính tổng 2 góc đó?
Chọn B.
Theo công thức cộng ta có:
Mà a và b là các góc nhọn suy ra
Câu 2:
Cho x và y là các góc nhọn, cotx = 3/4, cot y = 1/7. Tổng 2 góc đó là:
Chọn B.
Theo giả thiết cotx = 3/4, cot y = 1/7 nên tan x = 4/3 và tan y = 7
Theo công thức cộng ta có :
Mà x và y lại là các góc nhọn suy ra
Câu 5:
Rút gọn biểu thức C = 2( sin4x + cos4x + sin2x.cos2x) 2 - ( sin8x + cos8x) có giá trị không đổi và bằng
Chọn C.
Ta có: C = 2( sin4x + cos4x + sin2x.cos2x) 2 - ( sin8x + cos8x)
= 2 [ (sin2x + cos2x) 2 - sin2x.cos2x]2 - [ (sin4x + cos4x)2 - 2sin4x.cos4x]
= 2[ 1 - sin2x.cos2x]2 - [ (sin2x+ cos2x) 2 - 2sin2x.cos2x]2 + 2sin4x.cos4x
= 2[ 1- sin2x.cos2x]2 - [ 1 - 2sin2x.cos2x]2 + 2sin4x.cos4x
= 2( 1 - 2sin2xcos2x+ sin4x.cos4x) –( 1- 4sin2xcos2x+ 4sin4xcos4x) + 2sin4x.cos4x
= 1.
Câu 6:
Hệ thức nào sai trong bốn hệ thức sau:
Chọn D.
Ta đi xét các đáp án:
+ A đúng vì:
+ B đúng vì
+ C đúng vì
( chia cả tử và mẫu cho sin2α)
Câu 7:
Cho sin α = 3/5 và 900 < α < 1800. Tính giá trị của biểu thức 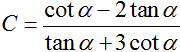
Chọn C.
Ta luôn có: sin2 α + cos2 α = 1 nên cos2α = 1- sin2 α = 16/25
Vì 900 < α < 1800. Nên cos α = -4/5 ; tanα = -3/4 ; cotα = -4/3.
Câu 8:
Cho 3sin4 α – cos4 α = 1/2. Tính A= 2sin4α – cos4 α.
Chọn B.
Theo giả thiết ta có: 3sin4 α – cos4 α = ½. Nên 3sin4 α – (1- sin2 α)2 = ½.
Hay 6sin4α - 2(1 - 2sin2α + sin4α) = 1
Suy ra: 4sin4α + 4sin2α - 3 = 0
Nên sin2α = 1/2
Ta lại có cos2α = 1 - sin2α = 1 - 1/2 = ½
Suy ra
Câu 11:
Cho tam giác ABC có góc A tù. Cho các biểu thức sau:
(1) M = sin A + sin B + sin C
(2) N = cosA. cosB. cosC
(3)
(4) Q = cotA.tan B.tan C
Số các biểu thức mang giá trị dương là:
Chọn B.
Ta có: góc A tù nên cos A < 0 ; sinA > 0 ; tan A < 0 ; cot A < 0;
Do góc A tù nên góc B và C là các góc nhọn có các giá trị lượng giác đều dương
Do đó: M = sinA + sinB + sinC > 0 ;
N = cosA,cosB.cosC <0 ;
. Vì A là góc tù nên 0<A<180
Q=cotA.tan B.tan C < 0.
Câu 14:
Cho góc α thỏa mãn tanα = 2 và 1800< α< 2700 . Tính P = cosα + sinα
Chọn A.
Ta có
Khi đó
Do đó,
Câu 17:
Cho góc α thỏa mãn: 3cosα+ 2sinα = 2 và sinα < 0. Tính sinα
Chọn A.
Ta có 3cosα+ 2sinα = 2 hay (3cosα+ 2sinα = 2 )2 = 4
Tương đương: 9 cos2 α + 12 cosα .sin α + 4sin2α = 4
Hay 5cos2α + 12 cosα .sin α = 0
Từ đó: cosα= 0 hoặc 5cosα + 12 sinα = 0
+ Nếu cosα = 0 thì sinα =1: loại ( vì sinα < 0).
+ 5cosα + 12 sinα = 0
ta có hệ phương trình
Câu 18:
Rút gọn biểu thức A = sin 2a.tan2a + 4sin2a - tan2a + 3cos2a
Chọn C.
Ta có A = sin 2a.tan2a + 4sin2a - tan2a + 3cos2a
= 3sin2a + 3cos2a = 3.
Câu 19:
Cho biểu thức: A = sin2(a + b) – sin2a - sin2b. Đưa biểu thức trên về dạng tích:
Chọn D.
Ta có: A = sin2(a + b) –sin2a - sin2b
= ( sina.cosb + cosa.sinb) 2 - sin2a - sin2b
= sin2a.cos2b + 2sina.cosb.cosa.sinb + cos2a.sin2b - sin 2a - sin2b
= sin2a( cos2b - 1) + sin2b( cos2a - 1) + 2.sina.cosa.sinb.cosb
= - sin2a.sin2b - sin2b.sin2a + 2.sina.cosa.sinb.cosb
= 2sina.sinb( cosa.cosb - sina.sinb) = 2.sina.sinb.cos( a + b).
Câu 21:
Rút gọn biểu thức A = cos2( x - a) + cos2x - 2cos a.cos x.cos( a - x).
Chọn A.
Ta có: A= cos2( x-a) + cos2x -2cos a.cos x.cos( a - x).
= cos( x - a) [ cos(x - a) – 2cosa. cosx] + cos2x
= cos( x - a) [ cos x.cosa + sina.sinx – 2cosa.cosx] + cos2x
= cos( x - a) [ -cos x.cosa + sina.sinx] + cos2x
= -cos( x - a) .cos( x + a) + cos2x
Câu 22:
Tính giá trị biểu thức P = ( sina + sinb) 2+ ( cosa + cosb) 2 biết a - b =
Chọn C.
Theo giả thiết ta có:
P = ( sina + sinb) 2 + ( cosa + cosb) 2
= sin2a + 2.sina.sinb + sin2b + cos2a + 2cosa. cosb + cos2b
= 2 + 2( sina.sinb + cos a. cosb)
= 2 + 2.cos( a - b) ( sử dụng công thức cộng)
Câu 23:
Cho A; B; C là ba góc của một tam giác. Hãy chỉ ra hệ thức sai
Chọn D.
Ta có:
A đúng.
A + B – C = π – 2C ⇒ cos(A + B – C) = cos(π – 2C) = -cos2C.
B đúng.
C đúng.
D sai.
Câu 24:
Cho A ; B; C là ba góc của một tam giác . Hãy chỉ ra hệ thức sai
Chọn C.
Ta có:
A đúng.
A + B + 2C = π + C ⇒ cos(A + B + 2C) = cos(π + C) = -cosC. B đúng.
A + C = π – B ⇒ sin(A + C) = sin(π – B) = sinB. C sai.
A + B = π – C ⇒ cos(A + B) = cos(π – C) = -cosC. D đúng.
Câu 25:
Cho A; B: C là ba góc của một tam giác không vuông. Hệ thức nào sau đây sai?
Chọn C.
Ta có :
A đúng.
+ tanA + tanB + tanC = tanA.tanB.tanC ⇔ -tanA(1 – tanBtanC) = tanB + tanC
⇔ tan A = -tan(B + C). B đúng.
+ cotA + cotB + cotC = cotA.cotB.cotC ⇔ cotA(cotBcotC – 1) = cotB + cotC
⇔ tanA = cot(B + C). C sai.
D đúng.

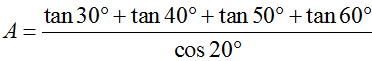 bằng :
bằng :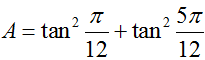 bằng :
bằng :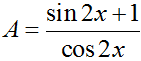 ta được
ta được