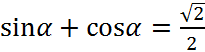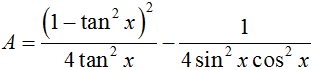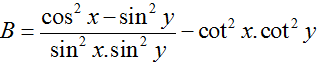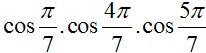100 câu trắc nghiệm Cung và góc lượng giác nâng cao (P2)
-
8834 lượt thi
-
25 câu hỏi
-
25 phút
Danh sách câu hỏi
Câu 1:
Trong mặt phẳng định hướng cho tia Ox và hình vuông OABC vẽ theo chiều ngược với chiều quay của kim đồng hồ, biết sđ( Ox; OA) = 300 + k.3600. Khi đó sđ ( OA; AC) bằng:
Chọn B.
Tia AO quay một góc 45 độ theo chiều âm( cùng chiều kim đồng hồ ) sẽ trùng tia AC nên góc sđ (OA, AC) = -450 + k3600, k ∈ Z.
Câu 2:
Trong mặt phẳng định hướng cho tia Ox và hình vuông OABC vẽ theo chiều ngược với chiều quay của kim đồng hồ, biết sđ ( Ox; OA) = 300 + k.3600 . Khi đó sđ (Ox; BC) bằng:
Chọn C.
Ta có: sđ( Ox; BC) = sđ( Ox; OA’) = 2100+ h.3600
Câu 3:
Trên đường tròn đơn vị, gọi các điểm A, B, C, D lần lượt là các điểm (1;0), (0;1), (-1;0), (0;-1). Cho L, M, N, P lần lượt là các điểm chính giữa các cung AB, BC, CD, DA. Cung có đầu mút trùng với A và có số đo . Mút cuối của trùng với điểm nào trong các điểm L, M, N, P?
Chọn A.
+ Vì L là điểm chính giữa
+ Vì N là điểm chính giữa
+ Ta có
Vậy L hoặc N là mút cuối của
Câu 4:
Trên đường tròn đơn vị, gọi các điểm A, B, C, D lần lượt là các điểm (1;0), (0;1), (-1;0), (0;-1). Cho M, N, P, Q lần lượt là các điểm chính giữa các cung AB, BC, CD, DA. Cung có đầu mút là A và mút cuối trùng với một trong bốn điểm M, N, P, Q. Số do của cung trên là
Chọn D.
+ Ta có số đo cung
+ Ta có
+ Để mút cuối cùng trùng với một trong bốn điểm M; N; P; Q thì chu kì của cung α là
Vậy số đo cung
Câu 5:
Biết OMB’ và ONB’ là các tam giác đều. Cung α có mút đầu là A và mút cuối là B hoặc M hoặc N. Tính số đo của α?
Chọn C.
+ Cung α có mút đầu là A và mút cuối là B nên
OMB’và ONB’ là các tam giác đều nên
+ Cung α có mút đầu là A và mút cuối là M hoặc N nên
+ Chu kì của cung α là
Từ (1), (2) ta có
Câu 8:
Giá trị đúng của 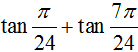 bằng :
bằng :
Chọn A.
Với 2 góc a và b thỏa mãn: cos a ≠ 0 và cos b ≠ 0 ta có
áp dụng nhận xét trên ta có:
Câu 9:
Cho góc α thỏa mãn tanα = 5. Tính P= sin4 α - cos4 α
Chọn D.
Ta có P = ( sin2α - cos2α) ( sin2α + cos2α) = sin2α - cos2α (*)
Chia hai vế của (*) cho cos2 α ta được
Tương đương: P(1 + tan2α) = tan2α - 1
Câu 10:
Biểu thức A = cos (-530) .sin( -3370) + sin3070.sin 1130 có giá trị bằng:
Chọn A.
Ta có;
A = cos (-530) .sin( -3370) + sin3070.sin 1130
= cos( - 530) .sin( 230- 3600) + sin( -530+ 3600) .sin( 900+ 230)
= cos ( -530) .sin230+ sin( -530) .cos 230
= sin ( 230- 530) = sin(- 300) = -1/2
Câu 12:
Cho góc α thỏa mãn ![]() và sinα + cosα > 0. Tính P = sin3 α + cos3 α.
và sinα + cosα > 0. Tính P = sin3 α + cos3 α.
Chọn A.
Ta có : P = sin3 α + cos3 α = ( sinα + cosα) 3 - 3sin α.cosα(sinα + cosα)
Ta có (sin α + cos α) 2 = sin2α + cos2α + 2sinα.cosα = 1 + 24/25 = 49/25.
Vì sin α + cosα > 0 nên ta chọn sinα + cosα = 7/5.
Thay vào P ta được
Câu 14:
Nếu sinx + cosx= 1/2 thì 3sinx + 2cosx bằng
Chọn A.
Từ giả thiết ta suy ra: (sinx+ cosx) 2 = ¼
Suy ra: 2sinx.cosx = -3/4 hay sinx.cosx = -3/8
Khi đó sinx; cosx là nghiệm của phương trình
Ta có: 3sinx+2cosx = sinx + 2(sinx+cosx) =sinx +2. =sinx+1.
+) Với
+) Với
Câu 15:
Một đường tròn có bán kính 15 cm . Tìm độ dài cung tròn có góc ở tâm bằng 300 là :
Chọn A.
Theo công thức tính độ dài cung tròn ta có nên
Ta có .
Câu 17:
Cho góc α thỏa mãn và tan α – cotα = 1. Tính P = tanα + cotα
Chọn C.
Ta có tan α – cotα = 1
Do suy ra tanα < 0 nên
Thay
và
vào P ta được
Câu 19:
Cho góc α thỏa mãn và . Tính P = sinα - cosα
Chọn D.
Ta có ( sinα - cosα) 2 + (sinα + cosα) 2 = 2( sin2α + cos2α) = 2.
Suy ra (sinα - cosα) 2 = 2 - ( sinα + cos α) 2 = 2 - 5/4 = 3/4.
Do suy ra sinα < cosα nên sinα - cosα < 0.
Vậy
Câu 20:
Rút gọn biểu thức A = cos2x.cot2x + 3cos2x - cot2x + 2sin2x không phụ thuộc vào x và bằng
Chọn A.
Ta có: A = cos2x.cot2x + 3cos2x - cot2x + 2sin2x
=( cos2x.cot2x - cot2x) + (2sin2x + 2cos2x) + cos2x
= cot2x( cos2x - 1) + 2 + cos2x
= - cot2x. sin2x + 2 + cos2x
= -cos2x + 2 + cos2x = 2
Câu 21:
Biểu thức rút gọn của 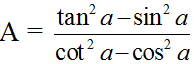 bằng :
bằng :
Chọn C.
Ta có: cot2a - cos2a
Tương tự ta có; tan2a - sin2a =
Do đó
Câu 25:
Cho A: B; C là các góc nhọn và tanA = 1/2, tanB = 1/5, tanC = 1/8,. Tổng A + B + C bằng
Chọn C.
Áp dụng công thức cộng ta có:
suy ra

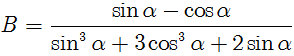
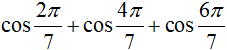 bằng :
bằng : là
là