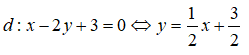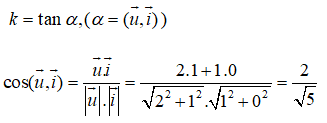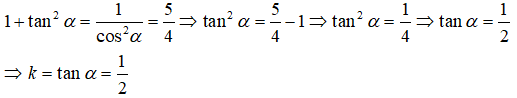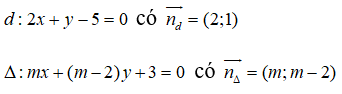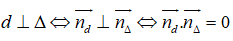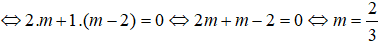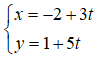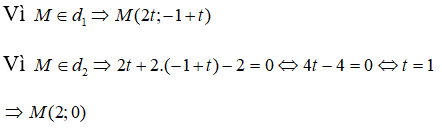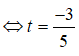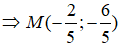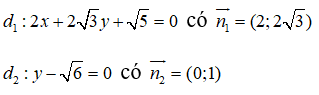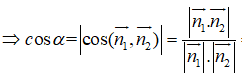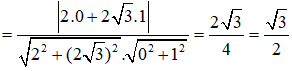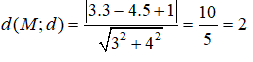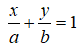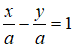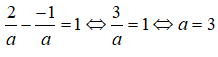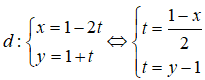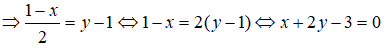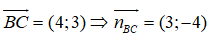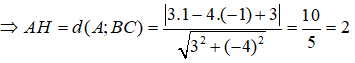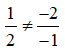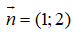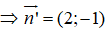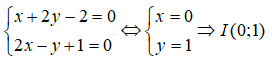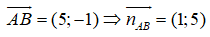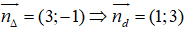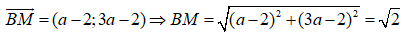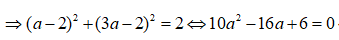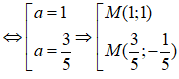Đề kiểm tra 45 phút Hình học 10 Chương 3 có đáp án (Đề 4)
-
1620 lượt thi
-
17 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Phần I: Trắc nghiệm
Cho đường thẳng d: x - 2y + 3 = 0. Trong các mệnh đề sau mệnh đề nào sai?
Đáp án: C
Vậy hệ số góc của d là k = 1/2
Câu 3:
Cho hai đường thẳng d: 2x + y - 5 = 0; Δ: mx + (m - 2)y + 3 = 0. Giá trị của m để d và Δ vuông góc với nhau là:
Đáp án: A
Ta có:
Câu 4:
Phương trình tham số của đường thẳng đi qua A(-2;1) và nhận u =(3;5) làm vecto chỉ phương là:
Phương trình tham số của đường thẳng đi qua A(-2;1) và nhận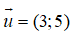 
làm vecto chỉ phương là:
Câu 5:
Tọa độ giao điểm của hai đường thẳng ; d2: x + 2y - 2 = 0 là:
Đáp án: B
Giả sử M là giao điểm của hai đường thẳng.
Câu 6:
Điểm M thuộc đường thẳng và cách điểm N(2;0) một khoảng ngắn nhất có tọa độ là:
Đáp án: B
M cách N một khoảng ngắn nhất khi M là hình chiếu vuông góc của N lên d
Gọi d’ là đường thẳng đi qua N và vuông góc với d. Khi đó, d’ đi qua N và nhận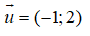 
làm vecto pháp tuyến
d': -(x - 2) + 2(y - 0) = 0 ⇔ -x + 2y + 2 = 0
Suy ra, M là giao điểm của d và d’
Vì M ∈ d ⇒ M(-1-t; 2t)
Vì M ∈ d'⇒ -(-1 - t) + 2.2t + 2 = 0 ⇔ 1 + t + 4t + 2 = 0 
Câu 7:
Cho hai đường thẳng d1: 2x + 2y + = 0 và d2: y - = 0. Góc giữa d1 và d2 có số đo bằng:
Đáp án: A
Gọi α là góc giữa hai đường thẳng d1, d2
⇒ α = 30
Câu 8:
Phương trình tổng quát của đường thẳng d đi qua A(-2;-1) và nhận làm vecto pháp tuyến là:
Đáp án: D
Phương trình tổng quát của đường thẳng d đi qua A(-2;-1) và nhận làm vecto pháp tuyến là: -(x + 2) + (y + 1) = 0 ⇔ -x + y - 1 = 0
Câu 9:
Khoảng cách từ điểm M(3;5) đến đường thẳng 3x - 4y + 1 là:
Đáp án B
Khoảng cách từ điểm M(3;5) đến đường thẳng 3x - 4y + 1 là:
Câu 10:
Trong (Oxy) cho A(2;-1) và d là đường thẳng đi qua A cắt Ox, Oy tại hai điểm M, N sao cho tam giác OMN cân. Phương trình đường thẳng d là:
Đáp án: D
Đường thẳng d đi qua A cắt Ox, Oy tại hai điểm M, N có dạng:
Vì tam giác OMN cân nên |a| = |b|
Vì d đi qua A(2;-1) nằm ở góc phần tư thứ tư nên b = -a, a > 0
Suy ra, đường thẳng MN có dạng:
MN đi qua A(2;-1) nên
Vậy đường thẳng MN có dạng:
Câu 11:
Cho phương trình tham số của đường thẳng . Phương trình tổng quát của d là:
Đáp án: A
Ta có:
Câu 12:
Cho tam giác ABC có A(1;-1); B(-1;0); C(3;3). Độ dài đường cao xuất phát từ đỉnh A của tam giác ABC bằng
Đáp án: A
Ta có: 
Đường thẳng BC đi qua B và có vecto 
là vecto pháp tuyến:
BC: 3(x + 1) - 4(y - 0) = 0 ⇔ 3x - 4y + 3 = 0
Gọi AH là đường cao của tam giác ABC
Câu 13:
Trong các đường thẳng có phương trình sau, đường thẳng nào cắt đường thẳng d: x - 2y + 1 = 0
Đáp án: D
Ta có: 
Do đó, đường thẳng d và đường thẳng ở đáp án D cắt nhau
Câu 14:
Cho đường thẳng d: x + 2y - 2 = 0 và điểm M(2;5). Điểm M’ đối xứng với M qua d có tọa độ là:
Đáp án: B
d: x + 2y - 2 = 0 có 
Gọi d’ là đường thẳng đi qua M và vuông góc với d 
⇒ d': 2(x - 2) - (y - 5) = 0 ⇔ 2x - y + 1 = 0
Gọi I là giao điểm của d và d’. Suy ra, tọa độ của I là nghiệm của hệ phương trình:
Vì M và M’ đối xứng nhau qua d nên I là trung điểm của MM’
⇒ M'(-2;-3)
Câu 15:
Cho tam giác ABC có các đỉnh A(1;0), B(2;-3), C(-2;4) và đường thẳng Δ: x - 2y + 1 = 0. Đường thẳng Δ cắt cạnh nào của tam giác ABC?
Đáp án: C
Thay lần lượt tọa độ của ba điểm A, B, C vào đường thẳng Δ ta được:
A: 1 - 2.0 + 1 = 2 > 0
B: 2 - 2.(-3) + 1 = 9 > 0
C: -2 - 2.4 + 1 = -9 < 0
Ta thấy: A và C nằm khác phía so với Δ nên Δ cắt cạnh AC
B và C nằm khác phía so với Δ nên Δ cắt cạnh BC
Câu 16:
Phần II: Tự luận
Trong (Oxy) cho hai điểm A(-3;1), B(2;0) và đường thẳng Δ: 3x - y - 2 = 0
a) Viết phương trình tham số của đường thẳng AB
b) Viết phương trình tổng quát của đường thẳng d đi qua A và vuông góc với Δ
c) Tìm tọa độ điểm M trên đường thẳng Δ sao cho BM =
Trong (Oxy) cho hai điểm A(-3;1), B(2;0) và đường thẳng Δ: 3x - y - 2 = 0
Viết phương trình tham số của đường thẳng AB
Đường thẳng AB đi qua B và có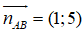 
là vecto pháp tuyến:
AB: (x - 2) + 5(y - 0) = 0 ⇔ x + 5y - 2 = 0
Viết phương trình tổng quát của đường thẳng d đi qua A và vuông góc với Δ
Δ: 3x - y - 2 = 0 có 
⇒ d: (x + 3) + 3(y - 1) = 0 ⇔ x + 3y = 0
Tìm tọa độ điểm M trên đường thẳng Δ sao cho BM = √2
Vì M ∈ Δ ⇒ M(a;3a-2)
Vậy có hai điểm M thỏa mãn yêu cầu đề bài.
Câu 17:
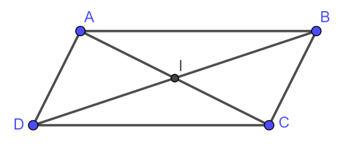
Trong (Oxy), cho hình bình hành ABCD có tâm I(1;2) và hai đường thẳng AB, AD lần lượt có phương trình là x + 3y - 6 = 0 và 2x - 5y - 1 = 0. Viết phương trình đường thẳng BC và CD.
Ta có: A là giao điểm của AB và AD. Do đó, tọa độ A là nghiệm của hệ phương trình:
Hình bình hành ABCD có tâm I nên I là trung điểm của AC và BD ⇒ C(-1;3)
Đường thẳng BC đi qua C và song song với AD
Vì BC song song với AD nên BC có dạng: 2x - 5y + c = 0, (c ≠ -1)
Vì C thuộc BC nên: 2.(-1) - 5.3 + c = 0 ⇒ c = 17(tm)
Vậy phương trình đường thẳng BC là: 2x - 5y + 17 = 0
Đường thẳng DC đi qua C và song song với AB
Vì DC song song với AB nên DC có dạng: x + 3y + c = 0, (c ≠ -6)
Vì C thuộc DC nên: -1 + 3.3 + c = 0 ⇒ c = -8(tm)
Vậy phương trình đường thẳng DC là: x + 3y - 8 = 0